In the field of artificial intelligence, large language models (LLMs) such as Claude, LLaMA, and DeepSeek are becoming increasingly powerful. However, adapting these models to specific tasks, such as legal Q&A, medical dialogues, or internal knowledge queries for a company, traditionally involves “fine-tuning” the model. This often entails significant computational overhead and high resource costs. Is there a way to achieve fine-tuning at a lower cost and with higher efficiency? Yes! This is precisely what we will discuss today — LoRA (Low-Rank Adaptation).
1. What is LoRA?
In simple terms, LoRA is a technique for fine-tuning large models through low-rank decomposition. The core idea is that, without changing the original model weights, we can adapt the model to new tasks by introducing only a small number of trainable parameters. Compared to traditional fine-tuning methods, LoRA significantly reduces computational resources and storage requirements, making it a “time-saving and labor-saving” fine-tuning tool.
To put it metaphorically, traditional fine-tuning is like “renovating” the entire model, requiring adjustments to every room; whereas LoRA is more like a “partial renovation,” where only key areas are modified with additional modules, allowing the house to look brand new. This “partial renovation” approach is not only efficient but also preserves the original knowledge of the model, avoiding performance degradation due to excessive adjustments.

2. The Mathematical Principles Behind LoRA: The Magic of Low-Rank Decomposition
Assuming we have a weight matrix W in a model, traditional fine-tuning requires adjusting the entire W, which is too large. LoRA’s approach is to represent the weight update as the product of two smaller matrices:
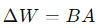
Where:

The calculation of the linear layer modified by LoRA is as follows:
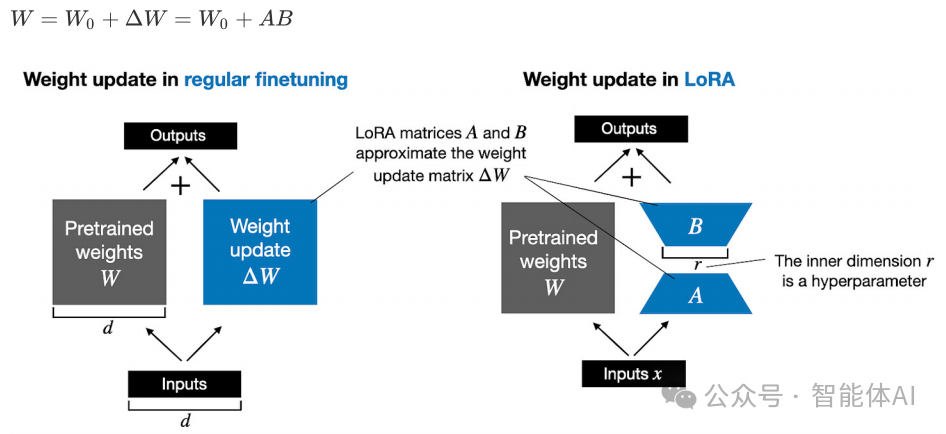
We only need to train the two small matrices A and B to achieve a similar effect as training the entire W! The key point is: the original weight W remains unchanged; we are merely adding a “patch” of small updates.
3. Why Train Only a Few Parameters and Still Achieve Good Results?
You might wonder: how can LoRA perform so well with so few parameters? The answer lies in the low intrinsic dimensionality characteristic of large models. The weight matrices of large language models often exhibit low-rank properties, meaning their core information can be expressed with fewer parameters. LoRA leverages this by capturing the key changes in weight updates through low-rank decomposition, thus achieving efficient fine-tuning with minimal parameters.
To illustrate, imagine the model’s weight matrix as a giant puzzle. Traditional fine-tuning attempts to adjust every piece of the puzzle, while LoRA discovers that adjusting just a few key pieces can refresh the entire picture. This “focusing on the essentials” strategy is the secret to LoRA’s efficiency.
4. How is LoRA Integrated into the Model?
In large language models, the Transformer is the fundamental architecture, and the attention module is a key component. LoRA is typically inserted in the following two places:
-
Linear mapping layers for Q and V in the attention module
-
Linear layers in the feedforward network
For example, in the attention module, if our original linear transformation for the query matrix Q uses the matrix WQ, LoRA will add a low-rank update module to become:

Where:
-
WQ: Pre-trained weights that will not be changed
-
BA: Trainable low-rank patch
-
α: Scaling factor to control the impact of LoRA
5. Why Fine-Tune Only Q and V?
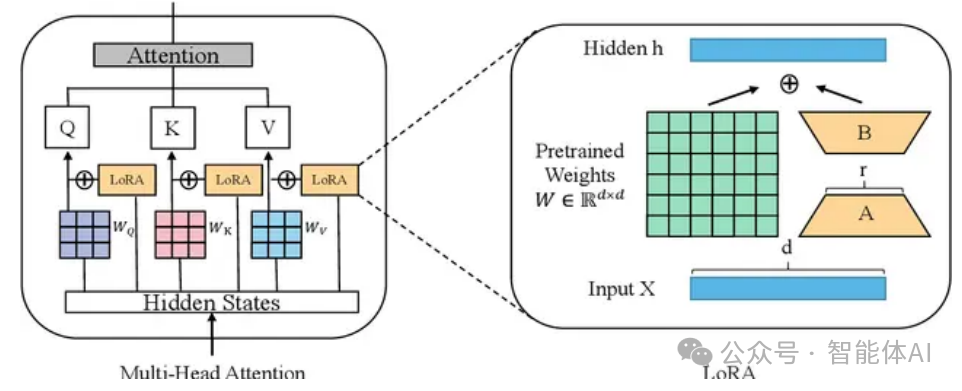
This is an empirical, validated optimization strategy for the following reasons:
-
Reduce computational load: Fine-tuning only Q and V, without touching K, can significantly lower the number of parameters.
-
Good performance: Q and V directly determine the weights and outputs of attention, having the greatest impact on model performance.
-
Lower risk of overfitting: Tuning fewer parameters is more stable.
-
Widely used in industry practice: Many successful application cases have chosen this “less is more” approach.
6. How Dramatic is the Parameter Savings?
For example, if the original weight matrix
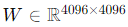
has a parameter count of 16.77 million, and using LoRA with r=8:
-
Original parameter count: 16,777,216
-
LoRA additional parameters: 4096×8+8×4096=65,536
-
Proportion: approximately 0.39%
This means that with less than 0.4% of the parameter count, we can achieve nearly the same effect.
7. Scaling Factor α: The Balancer of New and Old Knowledge
In LoRA, the scaling factor α is a very important tuning parameter. It determines how much influence the “patch” we add has on the model’s behavior:
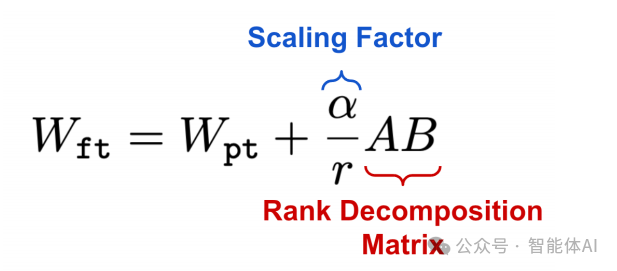
-
Default value is 1: Treats new and old weights equally.
-
Adjusting α value: If the model performs poorly on the new task, you can try increasing α to enhance LoRA’s effect.
When the rank r of LoRA is high, appropriately increasing α helps improve performance. This is akin to amplifying the “seasoning” we add, allowing the model to better adapt to the new recipe.
8. Conclusion
LoRA is like a clever “renovation master,” revitalizing large models with minimal changes. Its low-rank decomposition and scaling factor design are both elegant and practical, providing a new path for efficient fine-tuning. Whether you are an AI practitioner or a technology enthusiast, LoRA is worth exploring in depth — it is not only a technological breakthrough but also an important step towards the democratization of AI.