MLNLP community is a well-known machine learning and natural language processing community both domestically and internationally, covering audiences including NLP graduate students, university teachers, and industry researchers.

The vision of the community is to promote communication and progress between the academic and industrial sectors of natural language processing and machine learning, especially for beginners.

Source | PaperWeekly

Author | Taki@The University of Hong Kong

Nothing will work unless you do. ——Maya Angelou

This article mainly introduces how a paper is born. The basic information of the article is as follows:

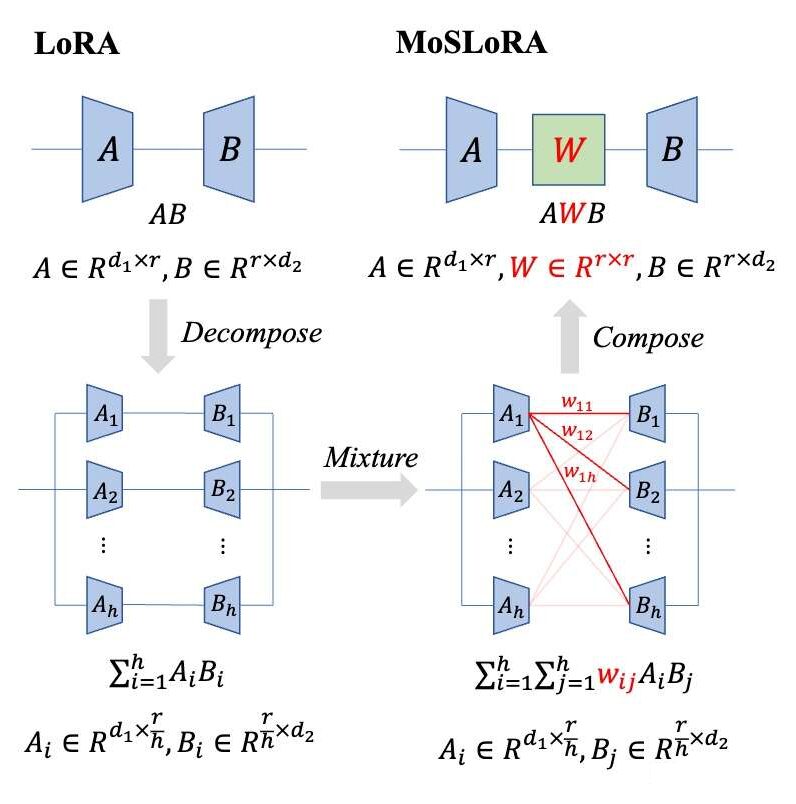
Integrating MoE into LoRA: The Birth of an Article

Paper Title:

Mixture-of-Subspaces in Low-Rank Adaptation

Paper Link:

https://arxiv.org/pdf/2406.11909

Code Link:

https://github.com/wutaiqiang/MoSLoRA

Introduction: A Mixer matrix is added to the traditional LoRA to mix information from different subspaces. The design is very simple:

Initial Thoughts

Interestingly, many articles have attempted to combine LoRA and MoE, treating LoRA as the expert of MoE and integrating it into the MoE structure. Some of these have been introduced previously, such as articles 1, 2, 3, 4. These articles undoubtedly view LoRA as an expert of MoE, which lacks motivation, affects the mergeability of LoRA, and slows down training.

Chatting with a colleague, they mentioned they had not seen an article that integrates MoE into LoRA. I was taken aback. What? Integrating MoE into LoRA means using the gate + multiple experts of MoE to create LoRA’s lora_A and lora_B?

The most intuitive design is:

Actually, coming up with this design is quite straightforward, as both LoRA and MoE are mature and simple designs.

Let’s not discuss whether there is motivation; after all, for a water article, one can always find some points. However, this design is somewhat inappropriate, why?

The core issue lies in the gate. MoE aims to train as many parameters as possible without significantly increasing computation, thus employing multiple experts and designing a gate router mechanism. However, LoRA already has a small number of parameters, and a high rank doesn’t necessarily yield better results, so piling on this parameter is indeed unnecessary.

Moreover, the benefit of LoRA is its ability to merge back to the original weights, with 0 latency during inference. This router gate is coupled with the input x, making it impossible to merge back, which introduces inference latency.

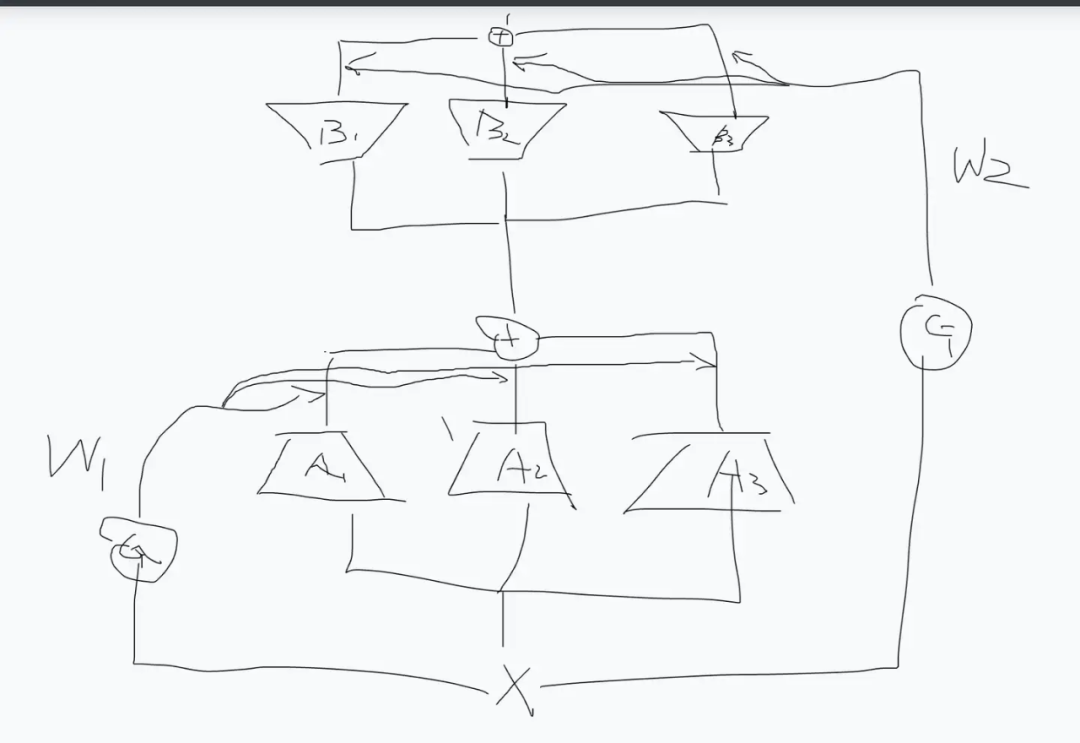
Removing the Gate, Going Directly

With the above analysis, the next step is naturally to remove the gate. To ensure mergeability, all experts must be used, transforming it into:

After this design, some concerns arose: although during inference, everyone can merge back to the original weights, all with 0 latency. However, during training, for instance, as illustrated in this diagram, the training parameters are more than three times the previous amount. (In today’s environment, this might attract criticism from reviewers).

Therefore, to maintain fairness, we cannot set it to r; each module must still be set to r/k, where the case in the diagram corresponds to r/3, so that the training parameters remain unchanged while inference maintains 0 latency.

This is the origin of the two-subspace-mixing method mentioned in the paper.

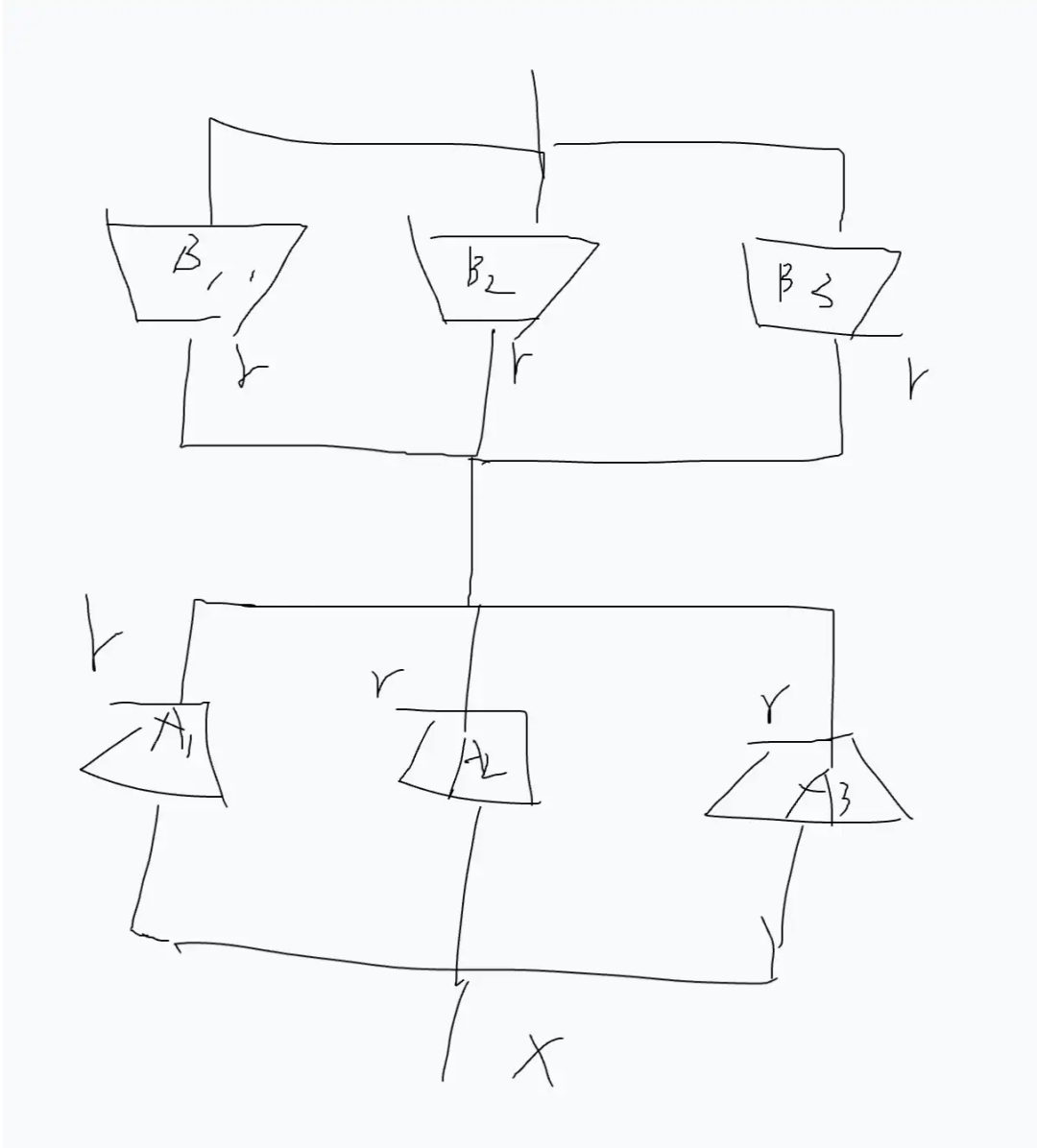
From the Perspective of ‘Multi-Head Attention’

Since each expert is set to a size of r/k, this resembles multi-head attention, with dimension splitting + parallel operation + final merging. This leads me to ponder: what is the relationship with multi-head attention? Can the original LoRA be decomposed equivalently?

Speaking of decomposition, there are two quantities that can be decomposed: one is rank and the other is the input dimension d. If we directly talk about multi-head, people might think of splitting d directly rather than splitting rank. However, we can analyze both types of splitting:

i) Splitting from the perspective of d:

The diagram shows the case of splitting d into 2 d/2. For better understanding, I deliberately drew it from a matrix perspective. From the perspective of matrix operations, after splitting in the d dimension, it is equivalent to passing through two A’s, summing, then passing through two B’s, and finally concatenating. These three perspectives are equivalent.

To be honest, there’s not much to improve in this regard.

ii) Splitting from the perspective of r:

Similarly, rank can also be decomposed. The above diagram illustrates the process of splitting rank into two sub-blocks. It can be seen that this is equivalent to two branches, each with rank=r/2, finally summing. This method is clearly more elegant than the previous method of splitting d.

From this perspective, a very simple improvement emerges:

The idea is simple: it’s about twisting the parallel branches in the middle together. From a formula perspective, it transforms from A1B1+A2B2 to (A1+A2)(B1+B2)=A1B1+A2B2+A1B2+A2B1.

This effectively adds two more terms. Let’s tentatively call this the twisted scheme.

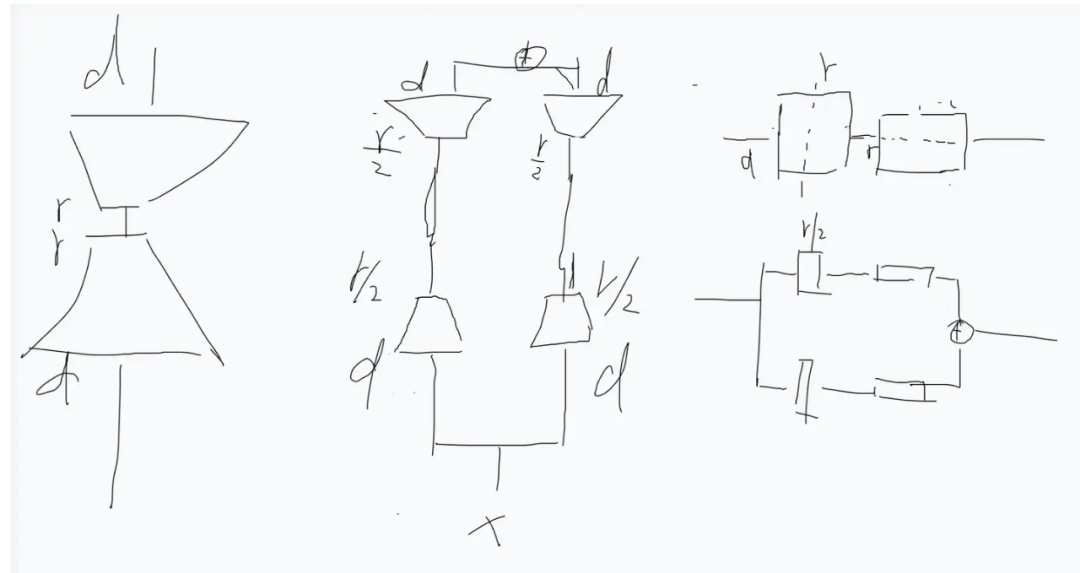
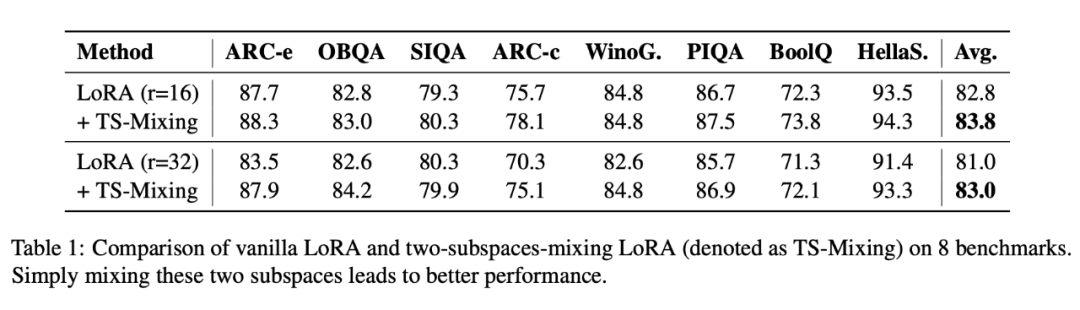
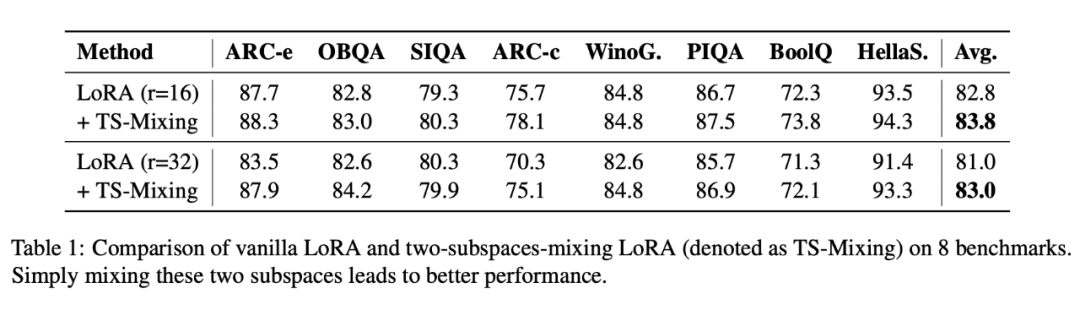
Phase Results, But Not Enough

With the above analysis, we began to conduct experiments:

Tuning LLaMA3 for commonsense reasoning, we found improvements.

However, there’s a problem: the code efficiency is not high. Drawing a few parallel lines and then twisting them is simple, but the implementation depends on how to achieve it. I initialized two experts to forward in sequence, hence the computation efficiency is low. Of course, we can also learn from the MHA code, first performing inference, then splitting the vectors (equivalent to combining two linear layers A1 and A2 in a forward pass, and splitting the vector afterward).

This inspired another thought: many operations here involve splitting and merging linear layers; our previous analyses focused on splitting and merging linear layers without considering vector splitting and merging operations. From a vector perspective, it is equivalent to:

The previously mentioned twisted operation is equivalent to splitting the r-dimensional vector, summing it to half its length, then copying and concatenating to obtain the final r’. From this perspective, this multi-expert twisted scheme is essentially a combination of operations on the r-dimensional vector.

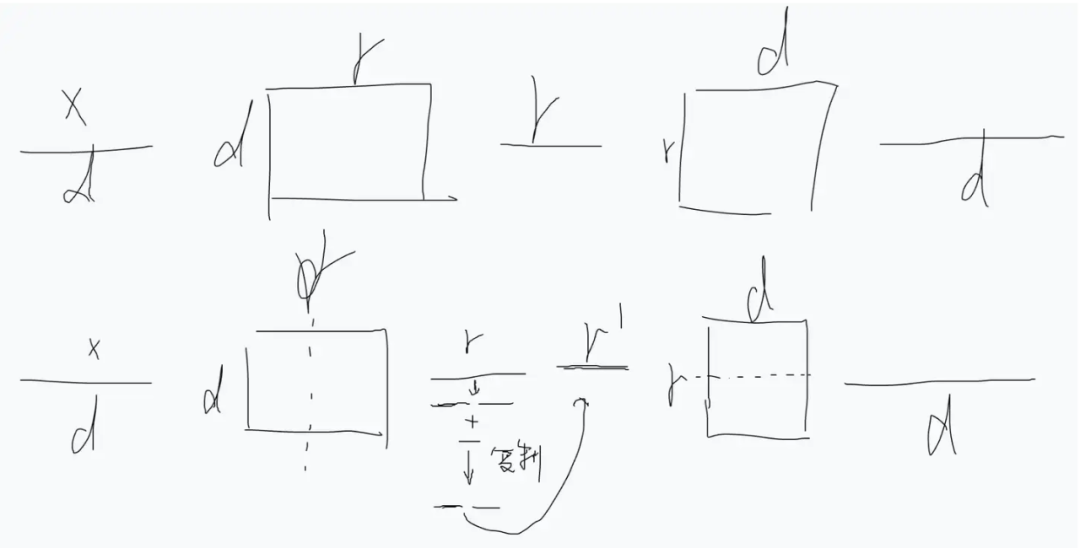
Introducing the Mixing Matrix

Since it adds a set of combined operations, what does this combination (r-dimensional vector, splitting, summing, and copying) look like in matrix form?

After some analysis, it’s not difficult to conclude that it’s equivalent to adding a fixed butterfly matrix factor in the middle (for more on butterfly matrix factors, refer to: https://weld.stanford.edu/2019/06/13/butterfly/).

Given this, is it possible to mimic Tri Dao’s approach and introduce a series of butterfly matrix factors? However, it seems unnecessary, as LoRA itself has a low computational cost, making such decomposition unnecessary; furthermore, delay might increase significantly (additionally, research has shown that butterfly matrix sequences are applied in the OFT series, i.e., BOFT).

Instead of going down the butterfly matrix sequence path, another intuitive idea is to upgrade this matrix to a learnable matrix. In my paper, I refer to this matrix as the Mixer matrix, therefore:

The original LoRA can be seen as using a fixed identity matrix as the Mixer, the middle twisted scheme is equivalent to inserting a fixed butterfly factor matrix as the Mixer, and the paper upgrades it to a learnable Mixer, where all matrix elements are learnable, which is the proposed MoSLoRA method.

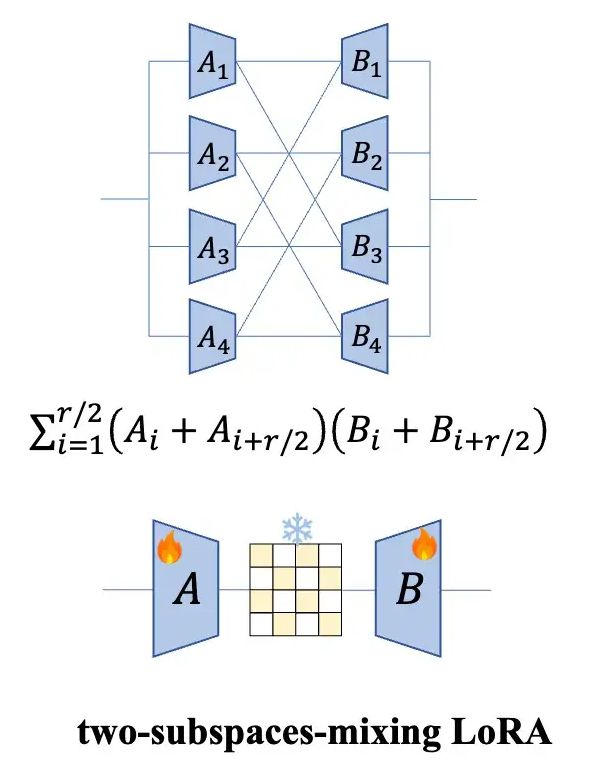
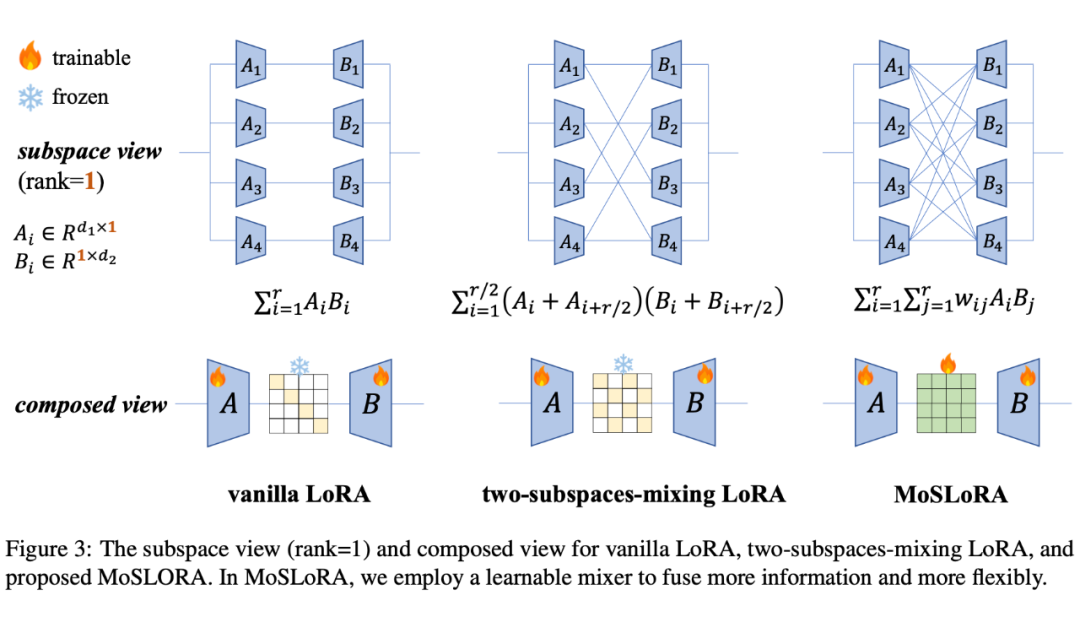
Note 1: This form is quite similar to AdaLoRA, but in AdaLoRA, the middle part is a feature value from SVD decomposition, and both front and back matrices have orthogonalization constraints added.

Note 2: While writing the paper, I discovered an excellent concurrent work on Arxiv: FLoRA: Low-Rank Core Space for N-dimension, which approaches the problem from the perspective of Tucker decomposition. Their thought process is clever and elegant; those interested can also check out their paper and interpretations.

Returning to the MoE Perspective

Returning to the MoE perspective means going back to the initial diagram of the paper:

We can simply understand the Mixer as the weight generated by the MoE gate, and this gate has several characteristics:

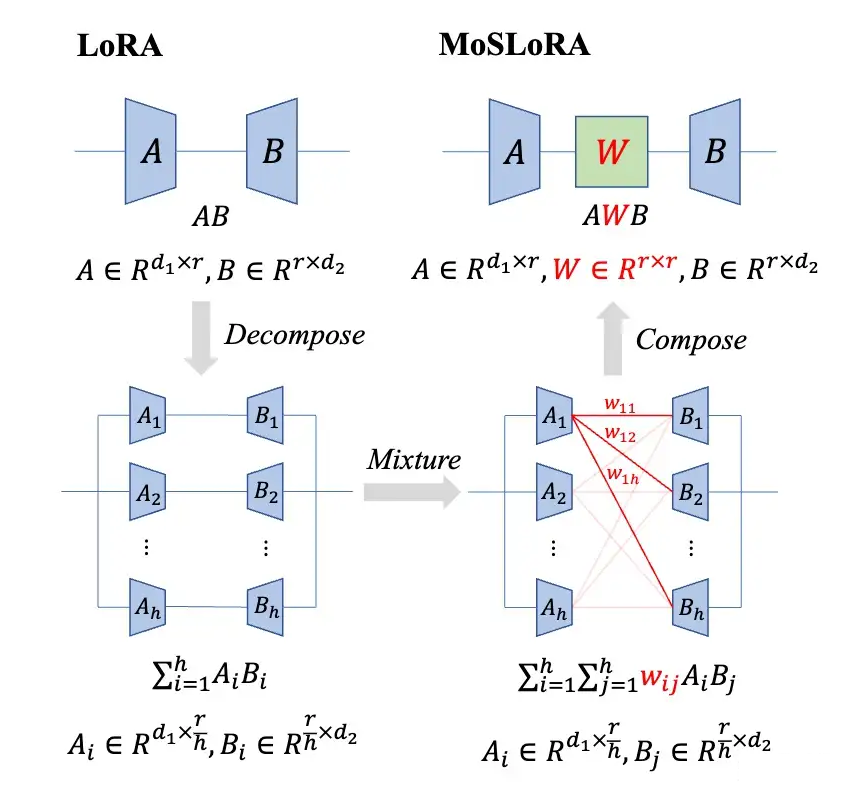
This weight is independent of the input, ensuring mergeability.
This weight is dense, meaning all experts are utilized, rather than the top-k selection of MoE.
The original vanilla LoRA can be viewed as having this Mixer matrix fixed to the identity matrix.

From this, we can also understand another thing:

[Multiple parallel LoRA branches select top-k outputs and then sum] This conventional LoRA+MoE design essentially means the Mixer possesses: i) each row is the same element ii) some rows are all zero iii) non-zero rows’ elements are determined by the input iv) non-mergeable properties.

Postscript

Having written this, I have clarified the entire thought progression process. Of course, the paper cannot be written this way; it would be too lengthy and difficult to understand. Even fewer people have the patience to read a blog post, let alone reviewers. However, I gained a lot from this entire thought process; something that seems complex at first can become so simple from a different perspective.

Supplementary Proof

Intuitively, inserting a W in the middle and merging AW as A’ means isn’t it the same as directly learning A’B?

Actually, it’s not the same; even if initialized equivalently, it doesn’t mean the subsequent optimization paths are consistent. Just like reparameterization, although it seems equivalent, the results learned are different. From this perspective, the Mixer can also be viewed as a form of reparameterization branch:

Where I is a fixed non-learning matrix. This effectively adds a parallel branch next to the original LoRA, consistent with reparameterization like RegVGG.

Of course, here is a simple proof of [the subsequent optimization paths being inconsistent]:

https://github.com/wutaiqiang/MoSLoRA/blob/main/MoSLoRA_proof.pdf

We can also see from the diagram:

Only when W is a fixed orthogonal matrix is it equivalent; otherwise, even if the initialization is consistent, the optimization process will differ.

In MoSLoRA, W is learnable, and we have analyzed the impact of initialization on the result.

Technical Community Invitation

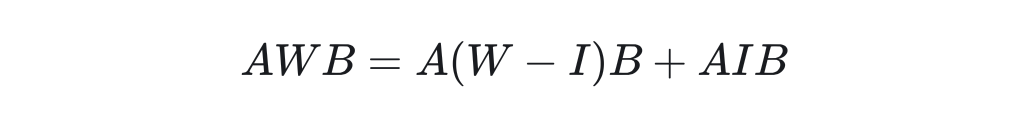
Integrating MoE into LoRA: The Birth of an Article

△ Long press to add the assistant

Scan the QR code to add the assistant WeChat

Please note: Name – School/Company – Research Direction

(e.g., Xiao Zhang – Harbin Institute of Technology – Dialogue System)

to apply for joining Natural Language Processing/Pytorch and other technical communities

About Us

MLNLP community is a grassroots academic community jointly established by scholars in machine learning and natural language processing from both domestic and international backgrounds. It has developed into a well-known community for machine learning and natural language processing, aiming to promote progress among the academic and industrial sectors and enthusiasts.

The community can provide an open exchange platform for practitioners’ further education, employment, and research. We welcome everyone to follow and join us.