
This article aims to understand the differences between two methods of fine-tuning large language models: full fine-tuning and Low-Rank Adaptation (LoRA). Both methods are used to adapt pre-trained models to specific downstream tasks, but they differ.
Fine-tuning is a key example of applying pre-trained large language models to downstream tasks. Recently, methods like Low-Rank Adaptation (LoRA) have been shown to achieve performance comparable to fully fine-tuned models while significantly reducing the number of trainable parameters.
This raises the question: are the solutions they learn truly equivalent?
With this question in mind, researchers from MIT conducted an in-depth exploration in their paper “LORA VS FULL FINE-TUNING: AN ILLUSION OF EQUIVALENCE”.

Paper link: https://arxiv.org/pdf/2410.21228v1
The authors study how different fine-tuning methods change the model by analyzing the spectral properties of the pre-trained model’s weight matrix.
The study found significant differences in the singular value decomposition structure of the weight matrices produced by full fine-tuning and LoRA, and the fine-tuned models exhibited different generalization behaviors when faced with tests outside the adapted task distribution.
Specifically, new high-rank singular vectors known as “intruder dimensions” appeared in the weight matrices trained with LoRA, which do not occur in full fine-tuning.
These results suggest that even when performing similarly on the fine-tuning distribution, the models updated using LoRA and full fine-tuning access different parts of the parameter space.
The authors delve into the reasons for the emergence of intruder dimensions in LoRA fine-tuned models, why they are undesirable, and how to minimize these effects.
Finally, the authors provide the following observations:
First, LoRA and full fine-tuning produce different parameter updates structurally, a difference arising from the presence of intruder dimensions. These intruder dimensions are singular vectors with large singular values and are approximately orthogonal to the singular vectors in the pre-trained weight matrix. In contrast, the fully fine-tuned model remains spectrally similar to the pre-trained model and does not contain intruder dimensions.
Second, behaviorally, LoRA fine-tuned models with intruder dimensions forget more of the pre-trained distribution compared to full fine-tuning and exhibit poorer robust continual learning capabilities: LoRA fine-tuned models with intruder dimensions perform worse outside the adapted task distribution, despite comparable distribution accuracy.
Finally, even when low-rank LoRA performs well on the target task, higher-rank parameterization may still be preferable. Low-rank LoRA (r ≤ 8) is suitable for downstream task distributions, while full fine-tuning and high-rank LoRA (r = 64) enhance the model’s generalization ability and robustness to adaptation. However, to leverage higher ranks, the LoRA updated model must be rank-stable.
Wharton School Associate Professor Ethan Mollick commented: It turns out that customizing a general LLM using LoRA (like how Apple tunes its built-in models) imposes far greater limitations on the LLM than fine-tuning, as they lose some generalization ability. The reason is that LoRA introduces undesirable intruder dimensions.
Differences Between LoRA and Full Fine-Tuning Models
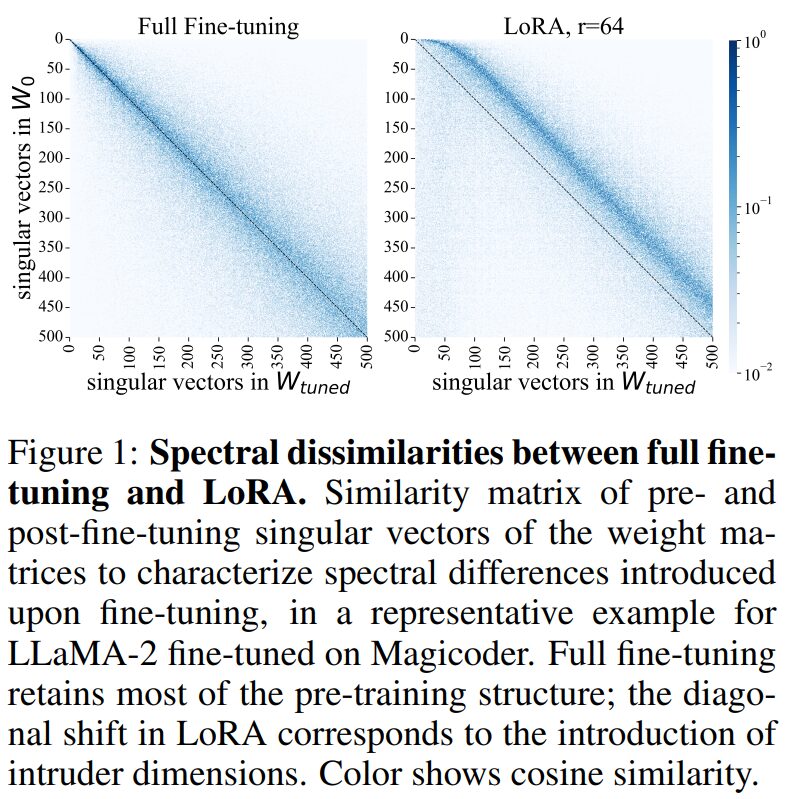
This article employs the singular value decomposition (SVD) of neural network parameters to understand how fine-tuning alters pre-trained weights.
Specifically, this paper measures the degree to which singular vectors from LoRA fine-tuned weight matrices map to singular vectors in fully fine-tuned weight matrices, using their cosine similarity. These relationships are illustrated in Figures 1 and 3, with colors indicating the cosine similarity between pre-trained and fine-tuned singular vectors.

In Figure 2 (b), it is observed that the singular vectors of LoRA and full fine-tuning differ significantly in similarity to the pre-trained singular vectors: the average cosine similarity of singular vectors in LoRA fine-tuned models to pre-trained singular vectors appears to be much lower than that of full fine-tuning.
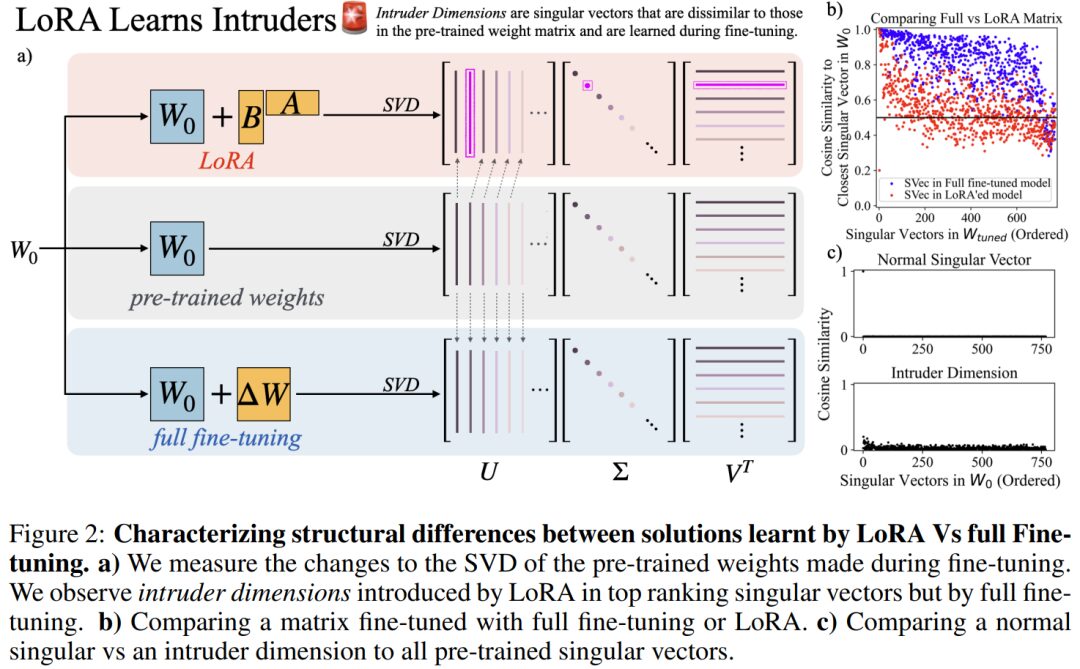
In Figure 2 (b), there is a unique red point in the lower left corner, which the authors name intruder dimensions, defined formally as follows:

LoRA fine-tuned models contain high-rank intruder dimensions, while fully fine-tuned models do not. To quantify the size of the set of intruder dimensions for a specific weight matrix, the authors use the algorithm shown in Figure 4.

Even when the learning performance of LoRA fine-tuned models is inferior to full fine-tuning tasks, intruder dimensions still exist.
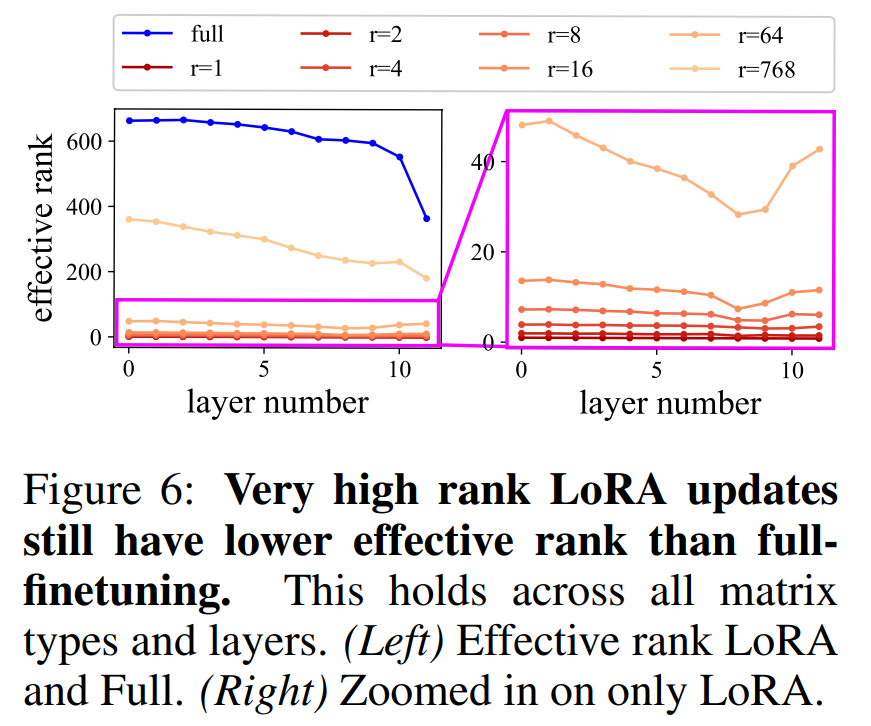
Observing Figures 5b, 5c, and 5d, we can clearly see that even with LoRA at r=256, high-rank singular vectors still exhibit intruder dimensions. Importantly, when r=2048, there are no intruder dimensions, instead showing curves very similar to full fine-tuning. This supports earlier findings: as the rank increases beyond a threshold, intruder dimensions disappear, and LoRA begins to resemble full fine-tuning.
Behavioral Differences Between LoRA and Full Fine-Tuning
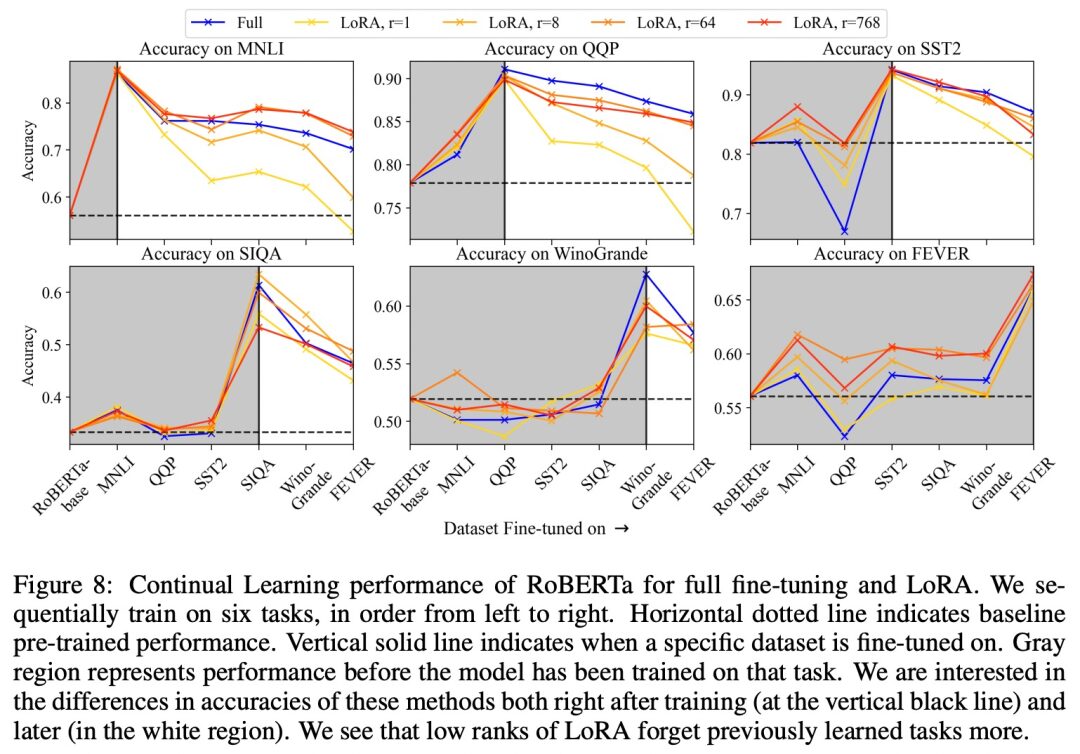
At lower ranks, LoRA exhibits poorer adaptability in continual learning processes, forgetting more previous tasks. This study sequentially trained RoBERTa on multiple tasks and measured performance changes when learning new tasks.
The study used the same training scheme and dataset as before, but fine-tuned in a continual learning environment using the following datasets (in order): MNLI, QQP, SST-2, SIQA, Winogrande, FEVER. After training on a particular dataset in the sequence, the LoRA weights were merged into the model and reinitialized before training on the next task to avoid being influenced by previous tasks.
After training on specific tasks, the study tested all tasks, retraining the classification head for each task before testing the test set. This allowed checking how the model performed on these tasks without actually changing the model itself.
The results are shown in Figure 8. Although LoRA initially performed comparably to full fine-tuning, smaller LoRA ranks consistently exhibited greater performance declines during continual learning. Notably, for the first three training datasets, when r = 1, the performance of LoRA dropped below the pre-trained baseline. As the LoRA rank increased, we observed a reduction in this forgetting behavior, becoming closer to full fine-tuning, and even less forgetting on MNLI after completing continual learning.
The overall situation is subtle: while in some cases, LoRA seems to forget less, for certain tasks (and certain ranks), it may actually forget more.
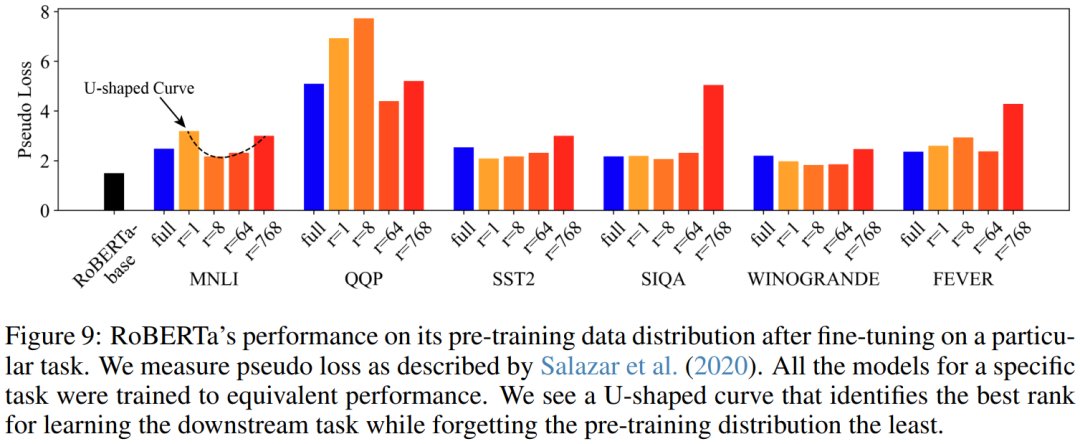
For LoRA models fine-tuned to equivalent test accuracy, a U-shaped curve can be observed, marking the optimal rank for downstream tasks while minimizing forgetting of the pre-trained distribution.
Figure 9 reports the measured pseudo-loss scores. A U-shaped trend can be seen between full fine-tuning and LoRA at r = 768.
Relative to full fine-tuning, both low-rank (r = 1) and high-rank (r = 768) lead to greater forgetting of the pre-trained distribution, while r = 64 results in less forgetting. That is, when r = 1, the LoRA fine-tuned model is affected by intruder dimensions and seems to forget more than r = 64, which has no intruder dimensions. However, when r = 768, the LoRA fine-tuned model also exhibits worse forgetting, indicating overfitting to the adapted task due to over-parameterization. When r = 8 and r = 64, forgetting is less than full fine-tuning.
For more content, please refer to the original paper.

Scan the QR code to add the assistant WeChat
About Us
