
Article Title:
MELoRA: Mini-Ensemble Low-Rank Adapters for Parameter-Efficient Fine-Tuning
https://arxiv.org/pdf/2402.17263

Rank of LoRA and LoRA Merging Reinitialization
First, we define the following symbols: weight weight and matrix as well as matrix then we have the formula for LoRA as follows::
1.1 Rank of LoRA
-
For matrices A and B, we have: at each training step, at each training step, -
For the product of A and B, we have: -
Thus::
1.2 Merging Reinitialization Method
Since: , if multiple lora weights are added together, there is hope to increase the rank of LoRA. The papers ReLoRA and CoLA both propose methods for merging and reinitializing LoRA weights at intervals during training, of course, they choose different theoretical explanations.
def _merge_lora(self) -> bool:
# Merge the lora weight into full rank weight if possible.
if self.has_lora_weights:
# Compute lora weight.
lora_weight = self._compute_lora()
if self.dora:
self.weight.data = self._apply_dora(self.weight, lora_weight)
else:
self.weight.data = self.weight.data + lora_weight
return True
return False
def merge_and_reset(self, new_rank: Optional[int] = None):
# If there is lora weight and it has been successfully merged, reinitialize the lora weight:
if new_rank is not None:
self.merge_and_del()
self.lora_rank = new_rank
self._init_lora_weights()
else:
if self._merge_lora():
std = (1 / self.in_features)**0.5
nn.init.normal_(self.weight_a, mean=0, std=std)
nn.init.zeros_(self.weight_b)
if self.quant:
self.weight_a_scaler = nn.Parameter(torch.Tensor(self.lora_rank))
self.weight_b_scaler = nn.Parameter(torch.Tensor(self.out_features))

MeLoRA
2.1 Motivation
2.2 Method
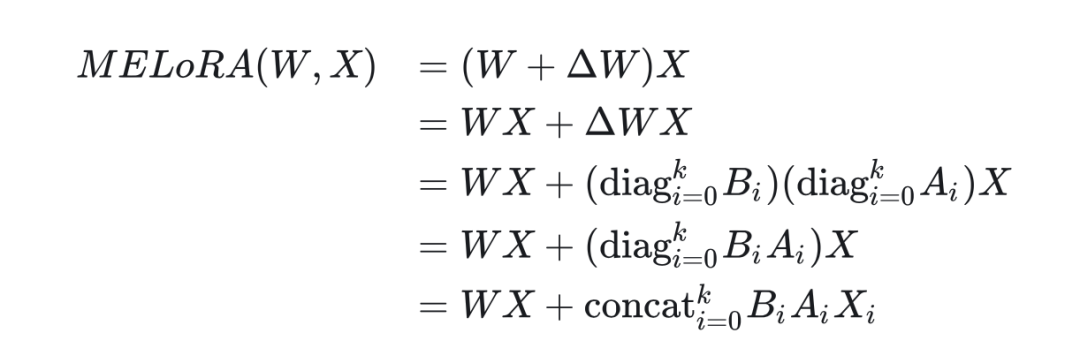

# @author: haonan he
# @date: 2024-08-21
""" Implements MELORA"""
from common.lora_modules.lora import *
class LinearWithMELoRA(LinearWithLoRA):
def __init__(self,
in_features: int,
out_features: int,
lora_rank: int = 4,
lora_scaler: float = 32.0,
lora_dropout: Optional[float] = None,
quant: bool = False,
weight_a_init_method: Optional[str] = None,
weight_b_init_method: Optional[str] = None,
me_lora_n_split: int = 2):
self.melora_n_split = me_lora_n_split
self.lora_rank = lora_rank
self.in_features = in_features
self.out_features = out_features
self._check_exact_division()
self.mini_lora_rank = int(self.lora_rank / self.melora_n_split)
self.mini_in_features = int(self.in_features / self.melora_n_split)
self.mini_out_features = int(self.out_features / self.melora_n_split)
super().__init__(in_features,
out_features,
lora_rank,
lora_scaler,
lora_dropout,
quant,
weight_a_init_method,
weight_b_init_method)
if quant:
print(f'Currently MELoRA is incompatible with quant, skipped quant')
def _check_exact_division(self):
if self.lora_rank % self.melora_n_split != 0:
raise ValueError(f"lora_rank ({self.lora_rank}) must be divisible by melora_n_split ({self.melora_n_split})")
if self.in_features % self.melora_n_split != 0:
raise ValueError(f"in_features ({self.in_features}) must be divisible by melora_n_split ({self.melora_n_split})")
if self.out_features % self.melora_n_split != 0:
raise ValueError(f"out_features ({self.out_features}) must be divisible by melora_n_split ({self.melora_n_split})")
def _init_lora_weights(self):
dtype = torch.int8 if self.quant else None
requires_grad = not self.quant
self.weight_a, self.weight_b =nn.ParameterList(), nn.ParameterList()
for _ in range(self.melora_n_split):
mini_weight_a = nn.Parameter(torch.empty((self.mini_lora_rank, self.mini_in_features), dtype=dtype), requires_grad=requires_grad)
mini_weight_b = nn.Parameter(torch.zeros((self.mini_out_features, self.mini_lora_rank), dtype=dtype), requires_grad=requires_grad)
self.weight_a.append(mini_weight_a)
self.weight_b.append(mini_weight_b)
self._init_weight(f'weight_a')
self._init_weight(f'weight_b')
def _init_weight(self, weight_name: str):
weight_list = getattr(self, weight_name)
init_method = getattr(self, f"{weight_name}_init_method")
init_kwargs = self.get_weight_init_kwargs(weight_name, init_method)
for weight in weight_list:
self.get_weight_init_method(**init_kwargs)(weight)
def _lora_forward(self, x: torch.Tensor, result: torch.Tensor) -> torch.Tensor:
lora_result = []
for i in range(self.melora_n_split):
mini_x = x[..., i*self.mini_in_features:(i+1)*self.mini_in_features]
mini_lora_result = F.linear(F.linear(self.lora_dropout(mini_x), self.weight_a[i]), self.weight_b[i])
lora_result.append(mini_lora_result)
lora_result = torch.cat(lora_result, dim=-1)
return result + self.lora_scaler * lora_result
def _compute_lora_weight(self):
if self.has_lora_weights:
# Compute lora weight.
weight_a = self._diagonal_concat_weight_a()
weight_b = self._diagonal_concat_weight_b()
lora_weight = self.lora_scaler * torch.matmul(weight_b, weight_a)
return lora_weight
def _diagonal_concat_weight_a(self):
weight_a = torch.zeros(self.lora_rank, self.in_features)
for i in range(self.melora_n_split):
start_row = i * self.mini_lora_rank
start_col = i * self.mini_in_features
weight_a[start_row:start_row+self.mini_lora_rank, start_col:start_col+self.mini_in_features] = self.weight_a[i]
return weight_a
def _diagonal_concat_weight_b(self):
weight_b = torch.zeros(self.out_features, self.lora_rank)
for i in range(self.melora_n_split):
start_row = i * self.mini_out_features
start_col = i * self.mini_lora_rank
weight_b[start_row:start_row+self.mini_out_features, start_col:start_col+self.mini_lora_rank] = self.weight_b[i]
return weight_b2.3 Results
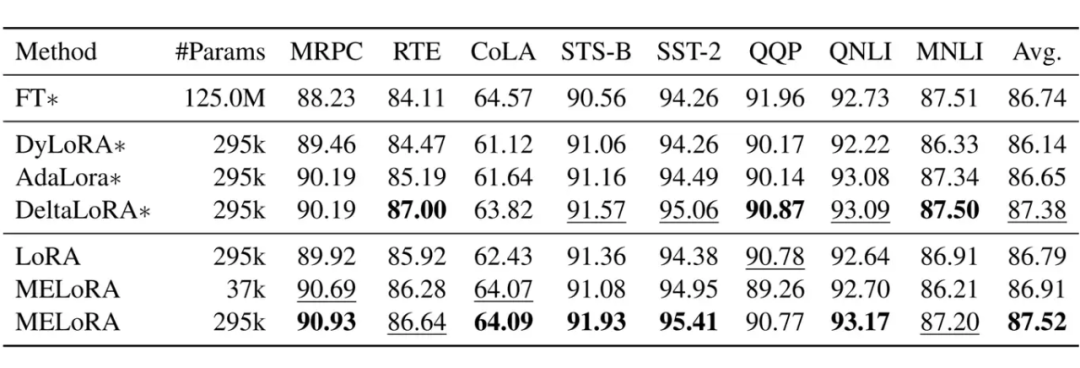
▲ MELoRA compared with AdaLoRA and other methods
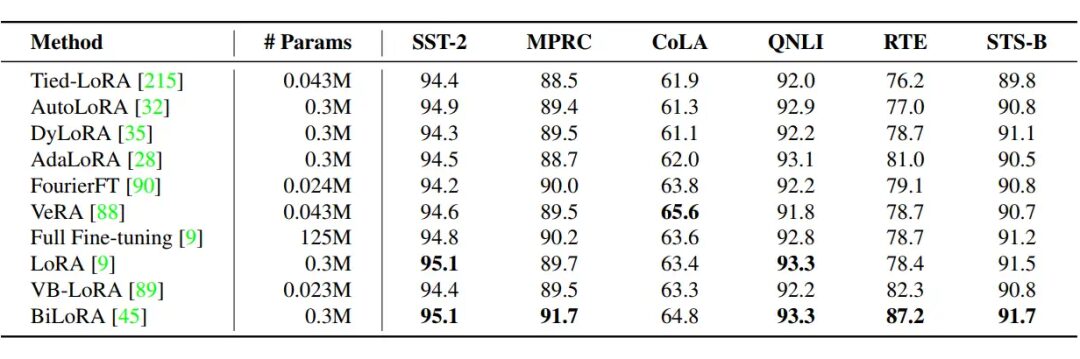
▲ Specific settings may not be consistent, for reference only