The Transient Trigonometric Harris Hawks Optimizer (TTHHO) is a hybrid optimization algorithm inspired by the Transient Search Optimizer (TSO) and the Harris Hawks Optimizer. This algorithm intelligently explores the search space and adaptively optimizes the positions of grid nodes while considering various constraints and objectives. It integrates the advantages of HHO, SCA, and TSO, aiming to improve convergence and solution quality. By adopting a hybrid approach, the TTHHO method is expected to produce more diverse solutions, as it can frequently make significant jumps within the search area to avoid getting trapped in local optima. This enhanced exploration capability allows for the generation of more varied solutions, making the search process more effective and comprehensive.

This achievement was published in 2024 in the comprehensive SCI Journal “Heliyon”. The TTHHO method exhibits better iterative optimization performance and excellent convergence.
1. Algorithm Principles
(1) Transient Search Optimizer
The TSO algorithm optimizes the search process through three stages: initialization, exploration, and exploitation. During initialization, search agents are randomly generated within a specified range. The exploration behavior of the algorithm is inspired by the oscillation of second-order RLC circuits near the zero point, while the development phase is derived from the exponential decay observed in first-order discharge circuits. The following figure shows the response of RLC to different system orders. A random number (r7) is used to balance exploration and exploitation, where r7 ≥ 0.5 emphasizes exploration, and r7 < 0.5 shifts the focus to exploitation. The preferred solution of TSO (ybest) replicates the final value or steady state of the circuit (x∞). The mathematical model for TSO’s development and exploration is given by the following equation:
In the equation, t represents time, where y(t) corresponds to the capacitor voltage v(t) of the RC circuit or the inductor current i(t) of the RL circuit. The time constant for the circuit is equal to the product of the resistance (R) and capacitance (C) of the RC circuit.
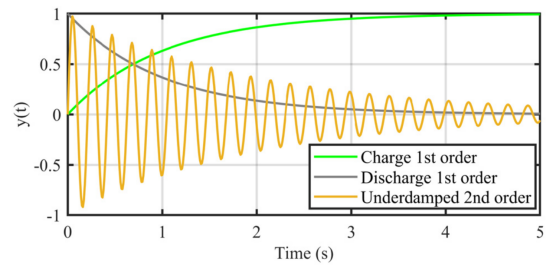
In the equation, ɑ is the damping coefficient, fd is the damping resonant frequency, and B1 and B2 are constants.
(2) Proposed Transient Trigonometric Harris Hawks Optimizer
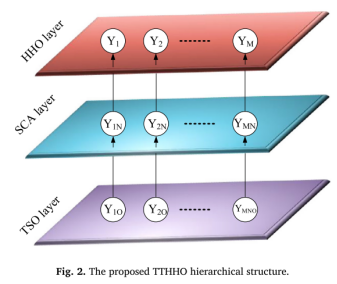
The following figure illustrates the hierarchical structure of the proposed TTHHO algorithm, where different layers are responsible for specific tasks. The bottom layer is represented by TSO, which is responsible for updating individuals generated by SCA in the middle layer. Subsequently, SCA updates the individuals generated by HHO in the top layer. In this hierarchical design, the top layer contains M search agents corresponding to M groups in the middle layer, where each group contains N SCA populations. Similarly, the bottom layer consists of 0 TSO populations. The optimization process begins with executing SCA and TSO in the middle and bottom layers to update the positions of individuals. The best solutions determined by each group in the bottom and middle layers are retained by the corresponding agents in the top layer. Using this best solution, the positions of HHO individuals in the top layer are updated, generating new equations representing the development and exploration phases. This hierarchical approach facilitates effective collaboration between different components, leading to significant improvements in solution quality and convergence behavior.
The following equation represents the exploration phase model of TTHHO when the prey’s escape energy is greater than or equal to |E| ≥ 1. The energy of the “prey” is derived from the hunting habits of Harris Hawks. For simplicity, the mathematical model of the behaviors occurring in the bottom and middle layers is represented by symbols A, B, C, and D, where t and T represent the current iteration and the maximum number of iterations, respectively.
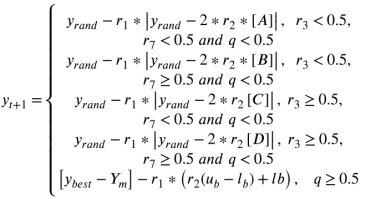
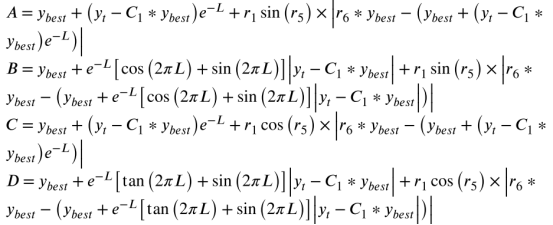
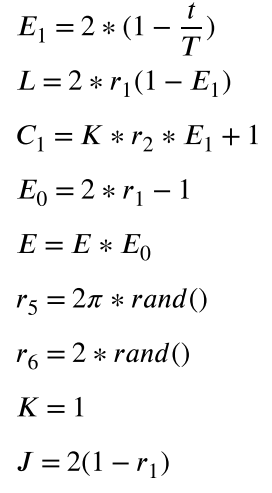
In the equation, r1, r2, r3, r4, r7, and r are uniformly distributed random parameters within ∈[0,1], where ybest is the currently obtained transient optimal solution, yt is the current solution, Ym is the overall mean, ub is the upper bound, and lb is the lower bound.
Similarly, HHO and TTHHO perform the exploitation phase by applying siege strategies. They are divided into hard siege, hard siege with progressive rapid diving, soft siege, and soft siege with progressive rapid diving. The switching between these strategies depends on the prey’s escape energy level in E ∈ [0,1] and the value of the randomly generated parameter r ∈ [0,1]. The mathematical representation of these strategies is further elaborated in the following formulas:
Hard siege: Inspired by the natural behavior of the hawk, its goal is the prey, which does not have enough energy to escape the pursuit. In this hybrid method, under the conditions of E < 0.5 and E ≥ 0.5, the following formulas represent this behavior.
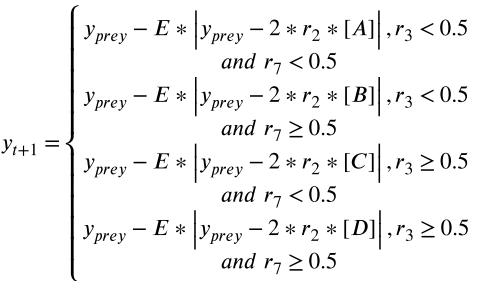
Where yprey represents the best position of the prey, and ybest represents the transient optimal solution.
Resilient siege with progressive rapid diving: This occurs when r < 0.5 and E < 0.5. In this case, the search agents exhibit behavior characterized by reduced exploration and increased exploitation as they focus on locating and capturing remaining prey with higher energy levels. This phase of the algorithm’s search is modeled by the following equation.
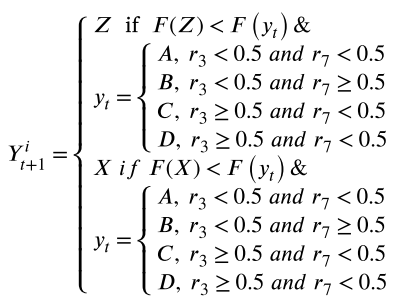
Where u and v are random variables ranging from 0 to 1, and m is a constant value of 1.5.
The pseudocode process corresponding to TTHHO is shown in the following figure.

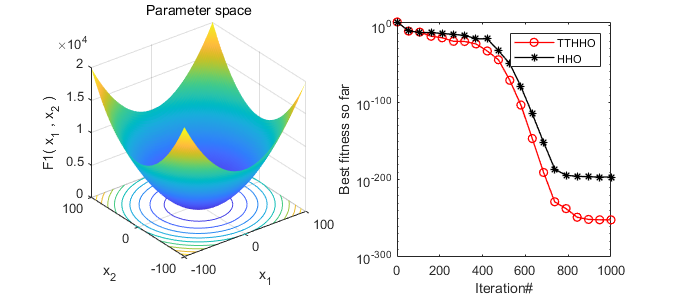
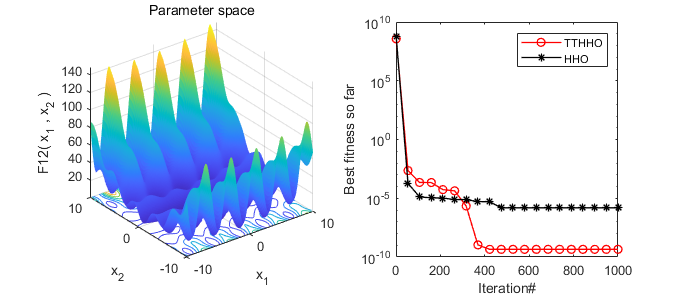
2. Results Presentation
A comparative display of the results of the Harris Hawks Optimizer (HHO) algorithm and the transient trigonometric Harris Hawks Optimizer (TTHHO) presented in this paper.
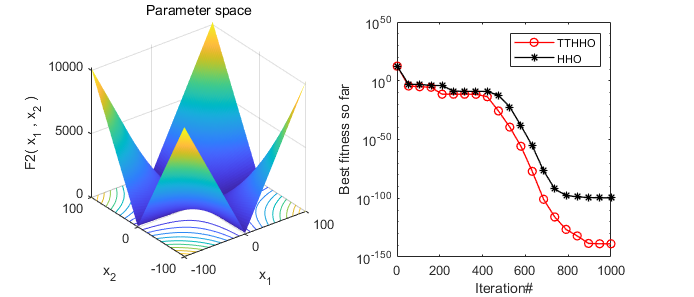
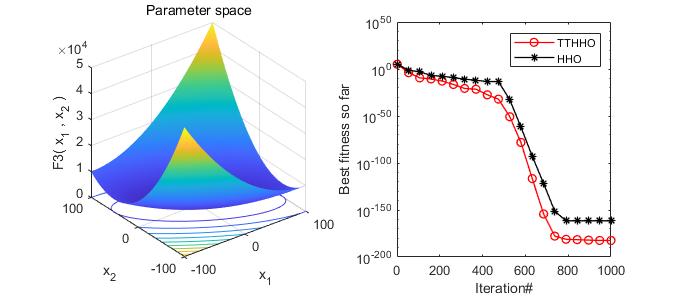
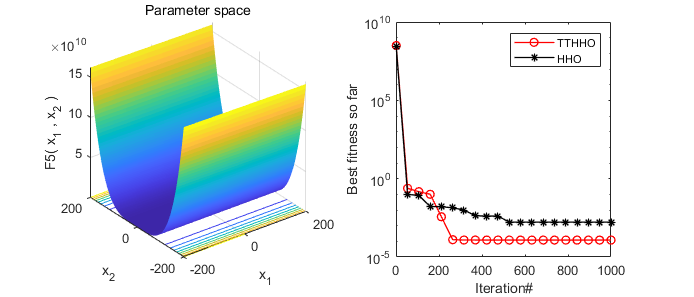
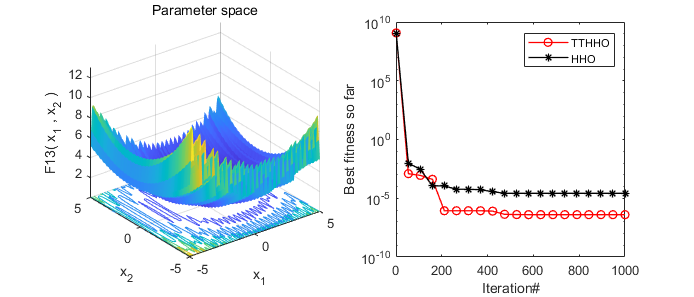
3. Core MATLAB Code
%% TTHHO Code %%
% Search WeChat public account: TTHHO to get more code
% Transient Trigonometric Harris Hawks Optimizer (TTHHO)
function [Rabbit_Energy,Rabbit_Location,CNVG]=TTHHO(N,T,lb,ub,dim,fobj)
disp('TTHHO is now tackling your problem')
tic
% initialize the location and Energy of the rabbit
Rabbit_Location=zeros(1,dim);
Rabbit_Energy=inf;
%Initialize the locations of Harris' hawks
X=initialization(N,dim,ub,lb);
CNVG=zeros(1,T);
t=0; % Loop counter
while t<t %="" boundaries="" check="" for="" fu="X(i,:)" i="1:size(X,1)">ub;FL=X(i,:)<lb;x(i,:)=(x(i,:).*(~(fu+fl)))+ub.*fu+lb.*fl; %="" %-1<e0<1="" 0,="" 1,="" 2,....="" a="" abs(escaping_energy)="" be="" best_voltage="Rabbit_Location;" c1="K*r2*E1+1;" can="" decreasing="" delta="rand()*(sin((pi/2)*(t/T))+cos((pi/2)*(t/T))-1);" e0="2*rand()-1;" e1="2*(1-(t/T));" end="" energy="" escaping="" escaping_energy="E1*(E0);" factor="" fitness="fobj(X(i,:));" fitness<rabbit_energy="" for="" harris'="" hawks="" i="1:size(X,1)" if="" is="" k="" l="2*E1*r1-E1;" location="" locations="" of="" r1="rand();r2=rand();" r10="2*rand;" r11="rand();" r3="rand();" r9="(2*pi)*rand();" rabbit="" rabbit_energy="fitness;" rabbit_location="X(i,:);" real="" show="" the="" to="" update="">=1
%% Exploration:
% Harris' hawks perch randomly based on 2 strategy:
q=rand();
rand_Hawk_index = floor(N*rand()+1);
X_rand = X(rand_Hawk_index, :);
if q<0.5
% perch based on other family members
if r3<0.5
if r11<0.5
X(i,:)=X_rand-rand()*abs(X_rand-2*rand()*(best_voltage+exp(-L)*(X(i,:)+(E1*sin(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
elseif r11>=0.5
X(i,:)=X_rand-rand()*abs(X_rand-2*rand()*(best_voltage+exp(-L)*(X(i,:)+(E1*cos(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage));
end
elseif r3>=0.5
if r11<0.5
X(i,:)=X_rand-rand()*abs(X_rand-2*rand()*(best_voltage+exp(-L)*(X(i,:)+(E1*sin(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
elseif r11 >= 0.5
X(i,:)=X_rand-rand()*abs(X_rand-2*rand()*(best_voltage+exp(-L)*(X(i,:)+(E1*cos(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage));
end
end
elseif q>=0.5
% perch on a random tall tree (random site inside group's home range)
X(i,:)=(Rabbit_Location(1,:)-mean(X))-rand()*((ub-lb)*rand+lb);
end
elseif abs(Escaping_Energy)<1
%% Exploitation:
% Attacking the rabbit using 4 strategies regarding the behavior of the rabbit
%% phase 1: surprise pounce (seven kills)
% surprise pounce (seven kills): multiple, short rapid dives by different hawks
r=rand(); % probability of each event
if r>=0.5 && abs(Escaping_Energy)<0.5 % Hard besiege
if r3<0.5
if r11<0.5
X(i,:)=(Rabbit_Location)-Escaping_Energy*abs(Rabbit_Location-(best_voltage+exp(-L)*(X(i,:)+(E1*sin(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
elseif r11>=0.5
X(i,:)=(Rabbit_Location)-Escaping_Energy*abs(Rabbit_Location-(best_voltage+exp(-L)*(X(i,:)+(E1*cos(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
end
elseif r3>=0.5
if r11<0.5
X(i,:)=(Rabbit_Location)-Escaping_Energy*abs(Rabbit_Location-(best_voltage+exp(-L)*(cos(L*2*pi)+tan(L*2*pi))*abs(X(i,:)+(E1*sin(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
elseif r11 >= 0.5
X(i,:)=(Rabbit_Location)-Escaping_Energy*abs(Rabbit_Location-(best_voltage+exp(-L)*(tan(L*2*pi)+sin(L*2*pi))*abs(X(i,:)+(E1*cos(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
end
end
end
if r>=0.5 && abs(Escaping_Energy)>=0.5 % Soft besiege
Jump_strength=2*(1-rand()); % random jump strength of the rabbit
if r3<0.5
if r11<0.5
X(i,:)=(Rabbit_Location-(best_voltage+exp(-L)*(X(i,:)+(E1*sin(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)))-Escaping_Energy*abs(Jump_strength*Rabbit_Location-(best_voltage+exp(-L)*(X(i,:)+(E1*sin(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
elseif r11>=0.5
X(i,:)=(Rabbit_Location-(best_voltage+exp(-L)*(X(i,:)+(E1*cos(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)))-Escaping_Energy*abs(Jump_strength*Rabbit_Location-(best_voltage+exp(-L)*(X(i,:)+(E1*cos(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
end
elseif r3>=0.5
if r11<0.5
X(i,:)=(Rabbit_Location-(best_voltage+exp(-L)*(cos(L*2*pi)+tan(L*2*pi))*abs(X(i,:)+(E1*sin(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)))-Escaping_Energy*abs(Jump_strength*Rabbit_Location-(best_voltage+exp(-L)*(cos(L*2*pi)+tan(L*2*pi))*abs(X(i,:)+(E1*sin(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
elseif r11 >= 0.5
X(i,:)=(Rabbit_Location-(best_voltage+exp(-L)*(tan(L*2*pi)+sin(L*2*pi))*abs(X(i,:)+(E1*cos(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)))-Escaping_Energy*abs(Jump_strength*Rabbit_Location-(best_voltage+exp(-L)*(tan(L*2*pi)+sin(L*2*pi))*abs(X(i,:)+(E1*cos(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
end
end
end
%% phase 2: performing team rapid dives (leapfrog movements)
if r<0.5 && abs(Escaping_Energy)>=0.5, % Soft besiege % rabbit try to escape by many zigzag deceptive motions
Jump_strength=2*(1-rand());
if r3<0.5
if r11<0.5
X1=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-(best_voltage+exp(-L)*(X(i,:)+(E1*sin(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
elseif r11>=0.5
X1=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-(best_voltage+exp(-L)*(X(i,:)+(E1*cos(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
end
elseif r3>=0.5
if r11<0.5
X1=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-(best_voltage+exp(-L)*(cos(L*2*pi)+tan(L*2*pi))*abs(X(i,:)+(E1*sin(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
elseif r11 >= 0.5
X1=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-(best_voltage+exp(-L)*(tan(L*2*pi)+sin(L*2*pi))*abs(X(i,:)+(E1*cos(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)));
end
end
if fobj(X1)<fobj(x(i,:)) %="" around="" dives="" else="" elseif="" hawks="" if="" improved="" levy-based="" move?="" perform="" r11="" r11<0.5="" r3<0.5="" rabbit="" rapid="" short="" the="" x(i,:)="X1;" x2="Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-(best_voltage+exp(-L)*(X(i,:)+(E1*sin(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)))+rand(1,dim).*Levy(dim);">=0.5
X2=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-(best_voltage+exp(-L)*(X(i,:)+(E1*cos(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)))+rand(1,dim).*Levy(dim);
end
elseif r3>=0.5
if r11<0.5
X2=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-(best_voltage+exp(-L)*(cos(L*2*pi)+tan(L*2*pi))*abs(X(i,:)+(E1*sin(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)))+rand(1,dim).*Levy(dim);
elseif r11 >= 0.5
X2=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-(best_voltage+exp(-L)*(tan(L*2*pi)+sin(L*2*pi))*abs(X(i,:)+(E1*cos(r9)*abs(r10*best_voltage-X(i,:)))-C1*best_voltage)))+rand(1,dim).*Levy(dim);
end
end
if (fobj(X2)<fobj(x(i,:))) %="" %%="" &&="" '="" ',="" (fobj(x2)<fobj(x(i,:))),="" 100="" <="" ___________________________________="" abs(escaping_energy)<0.5="" account:="" around="" author-amqymhbs="" average="" be="" besiege="" best="" beta="1.5;" by="" cnvg(t)="Rabbit_Energy;" code="" deceptive="" decrease="" display(['at="" dives="" docs.qq.com="" du3njykf5twdfunpu="" else="" end="" escape="" every="" fitness="" fobj(x1)<fobj(x(i,:))="" free="" function="" get="" hard="" hawks="" https:="" if="" improved="" is="" iteration="" iterations="" jump_strength="2*(1-rand());" levy-based="" list:="" location="" many="" mbd.pub="" mod(t,100)="0" more="" motions="" move?="" num2str(rabbit_energy)]);="" num2str(t),="" o="" of="" official="" perform="" print="" progress="" prohibition="" prosecuted!!!!!!!="" public="" r<0.5="" rabbit="" rapid="" resale,="" search="" sheet="" short="" sigma="(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);" store:="" t="t+1;" the="" their="" to="" toc="" try="" tthho="" u="randn(1,d)*sigma;v=randn(1,d);step=u./abs(v).^(1/beta);" violators="" wechat="" will="" with="" work="" x(i,:)="X2;" x1="Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-mean(X));" x2="Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-mean(X))+rand(1,dim).*Levy(dim);" zigzag=""></fobj(x(i,:)))></fobj(x(i,:))></lb;x(i,:)=(x(i,:).*(~(fu+fl)))+ub.*fu+lb.*fl;></t>References
[1] Abdulrab H, Hussin F A, Ismail I, et al. Energy efficient optimal deployment of industrial wireless mesh networks using transient trigonometric Harris Hawks optimizer[J]. Heliyon, 2024, 10(7).
Get Complete Code
Reply with the keyword:
TGDM813
Get more code:

Or copy the link to jump: https://docs.qq.com/sheet/DU3NjYkF5TWdFUnpu