The Effective Number of Bits (ENOB) of an ADC is one of the key indicators for measuring the actual performance of an Analog-to-Digital Converter (ADC). This article first provides a simple theoretical foundation, followed by examples illustrating how to calculate signal power, noise distortion power, and subsequently obtain the Signal-to-Noise and Distortion Ratio (SINAD) and the effective number of bits of the ADC, to help bridge theory with practice and inspire engineering endeavors.
1. Definition
The definition method of effective bits varies according to requirements, and the measurement methods differ slightly. The mainstream method currently considers noise and harmonic distortion, calculating the effective number of bits based on the SINAD. ENOB reflects the effective resolution that the ADC can provide. For example, a nominal 10-bit ADC may have an ENOB of only 8 bits due to noise and distortion, indicating that its actual performance is equivalent to that of an ideal 8-bit ADC.
2. Measurement Method
1. Signal Input
Input a clean, high-precision sine wave signal with an amplitude close to the full scale of the ADC (to avoid distortion).
2. Data Acquisition
To reduce the impact of spectral leakage, we set the sampling rate to the full period of the signal, ensuring that the signal is a pure spectral line, with the number of samples being N (usually a power of 2, such as 8192, which facilitates fast FFT processing).
3. Data Analysis
Perform an FFT transformation on the time-domain data, and based on the spectral line position, calculate the Signal-to-Noise and Distortion Ratio (SINAD): the ratio of the power of the fundamental signal to the total power of noise and harmonic distortion, noting that the unit here is dB.
4. Calculate ENOB
According to the formula: ENOB=(SINAD – 1.76)/6.02, where 1.76 dB is the reference value for the SNR of an ideal ADC (corresponding to 1 bit of the sign bit).
3. Consideration of Practical Factors
1. Signal Quality
The input sine wave should have low distortion and low noise to avoid introducing additional errors.
2. Amplitude Setting
The signal amplitude should be close to full scale (e.g., -0.5 dBFS), avoiding overload while ensuring optimal SNR.
3. Optimization of Spectral Analysis Parameters
The number of samples is recommended to be 2n (e.g., 8192 points), with integer multiple sampling resulting in a line spectrum, allowing for no window function. Ensure that the spectral resolution is high enough to distinguish between the fundamental and harmonic frequencies.
4. Multiple Measurements and Averaging
Average the ENOB from multiple measurements to reduce the impact of random noise.
4. Practical Example
Due to limitations in obtaining test data, this example illustrates the testing principles from a signal processing perspective and does not fully reflect the pure performance of the ADC’s effective bits. A test system based on a 12-bit ADC, with a sampling frequency of 200 MHz and a signal frequency of 12.5 MHz, has a sampling frequency that is 16 times the signal frequency. The number of samples is 8192, thus 12.5 MHz = 200 MHz / 16. The time-domain waveform and frequency spectrum of the acquired signal are shown below.
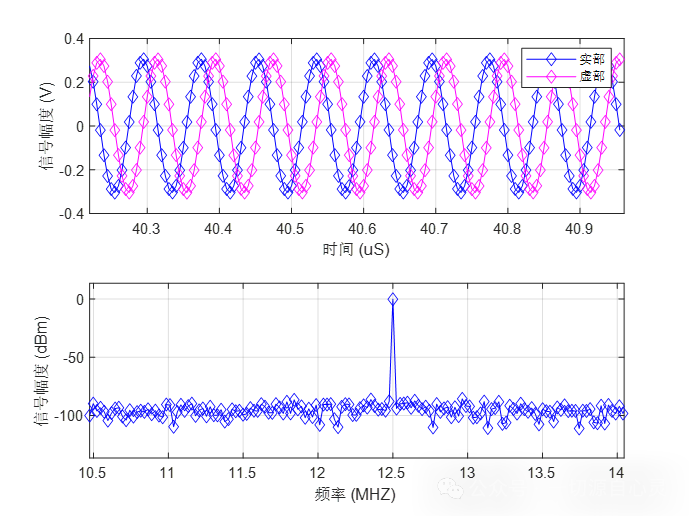
The signal power is calculated using the following MATLAB code:

The noise and distortion power is calculated using the following MATLAB code for cumulative power, with the basic principle being to deduct the total power after the signal:

If the measured SINAD is 57.3 dB, then:
ENOB = (57.3 – 1.76)/6.02 ≈ 9.2 (bits)
The obtained data indicates that the actual performance of the ADC is equivalent to that of an ideal 9.2-bit ADC.
5. Conclusion
The effective number of bits of an ADC reflects its dynamic performance. To measure the effective performance of an ADC in practical applications, it is essential to strictly control the independence of ADC testing, signal quality, sampling conditions, and data analysis methods to ensure accurate results.
(If you find this helpful, please help by sharing and following me, WeChat public account: Everything Comes from the Heart, thank you!)
(Feel free to directly share the link to this article for mutual learning and progress)