Gift to Readers

Conducting research involves a profound system of thought, requiring researchers to be logical, meticulous, and earnest. However, effort alone is not enough; often leveraging existing resources is more important. Additionally, one must have innovative and inspirational points of view. It is recommended that readers browse through the content in order to avoid suddenly falling into a dark maze without finding their way back. This article may not reveal all the answers to your questions, but if it can clarify some of the doubts that arise in your mind, it may create a beautiful sunset of insights. If it brings you a storm in your spiritual world, then take the opportunity to brush off the dust that has settled on your “lying flat” mindset.
Perhaps, after the rain, the sky will be clearer…



01

Overview




The cycle life model of graphite-lithium iron phosphate batteries
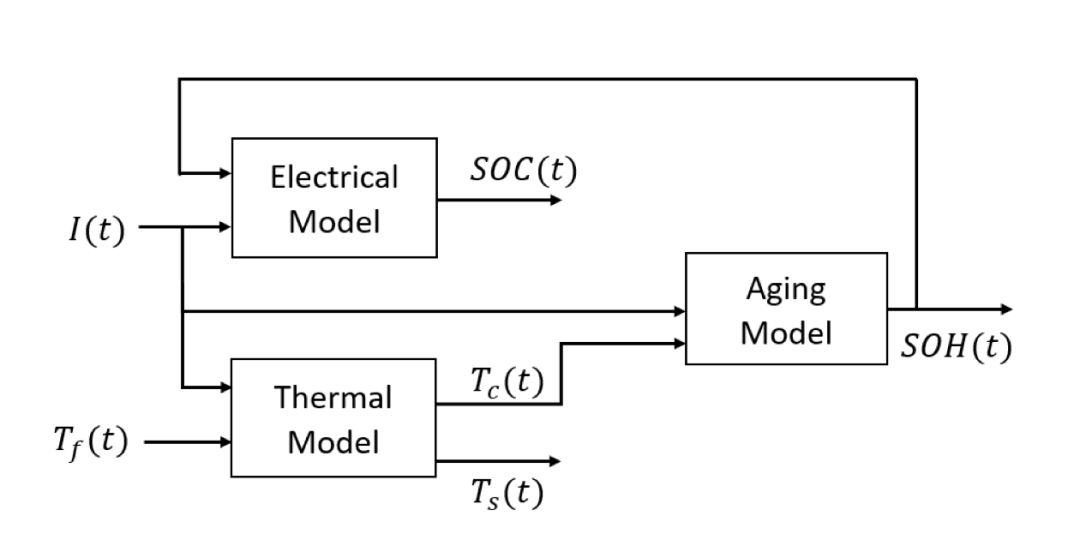
Batteries are widely used in various electronic devices and vehicles, serving as a key technology for storing clean and safe energy. Among the many types of batteries, lithium-ion batteries stand out due to their excellent specific energy density and volumetric energy density. To ensure the safe operation of lithium-ion batteries, estimating the State of Charge (SOC) and State of Health (SOH) is of utmost importance. Therefore, the goal of this project is to design a robust observer for estimating the SOC and SOH of lithium-ion batteries. In this project, an equivalent circuit model is used for battery modeling, with current and ambient temperature as inputs and voltage as output. The equivalent circuit model consists of three parts: electrical model, thermal model, and aging model. To ensure the accuracy of state estimation, the Extended Kalman Filter (EKF) is applied and tested in the project. The battery system is constructed and simulated using MATLAB. The optimal observer constructed in this project is the Voltage-Temperature (VT) observer, which can accurately observe SOC and has strong robustness; while SOH can be observed through an open-loop observer. The robustness of the designed observer is tested using incorrect initial estimates and erroneous model parameters.
Introduction
Motivation and Background
In practical applications, identifying the operational and aging conditions of batteries has always been a highly desired yet challenging goal. This goal involves multiple complex processes under intricate working conditions and environments. Therefore, we need an accurate method to observe the State of Charge (SOC) and State of Health (SOH) of lithium-ion batteries. Additionally, batteries typically operate under varying temperature and aging conditions. Thus, it is necessary to establish a battery observation system to monitor the operational and aging conditions of the battery. However, potential challenges exist. We need to express a multi-control problem through mathematical equations, integrating electrical, thermal, and aging models. Furthermore, since all team members major in civil systems, the lack of electrical engineering background knowledge may pose a significant challenge. However, the course CE 291F (Control and Optimization of Distributed Parameter Systems) we previously studied has been very helpful for this project. It provided us with relevant background knowledge on partial differential equations, conservation laws, linear stability, Kalman filtering, etc. We all have experience in constructing, controlling, and optimizing systems, including quenching processes, thermal diffusion, and the Lighthill-Whitham-Richards model.
Focus of the Study
In this project, we will focus on the SOC and SOH of lithium-ion batteries. Based on the equivalent circuit, we will develop electrical, thermal, and aging models for the observation system. Since battery monitoring and management may be key to future design innovations due to their limiting characteristics, our system may play an important role in this field and significantly contribute to energy conservation and efficiency improvement.
Literature Review
Due to the nonlinear characteristics of batteries, their behavior is difficult to predict, leading to numerous attempts to model and estimate the internal states of batteries. To better describe battery behavior, reference [1] introduced a lumped parameter electro-thermal model to capture the correlation between thermal and electrical behaviors; reference [2] established a semi-empirical cycle life model to study the characteristics of capacity loss. Combining these two models, reference [3] developed a coupled electro-thermal aging model to capture the dynamic behavior of lithium iron phosphate batteries. This model provides a reasonable assumption for battery behavior, which we will discuss in detail in the mathematical model section, while also providing an open-loop observer for SOC and SOH. Inspired by the materials from the CE 295 course, we attempt to further explore more possible methods for estimating battery states.
Main Contributions
Based on the aforementioned thermal-electrical-aging model, we constructed a robust observer that provides users with an efficient method to monitor the SOC and SOH of batteries.
1. Technical Description
1.1 Mathematical Model
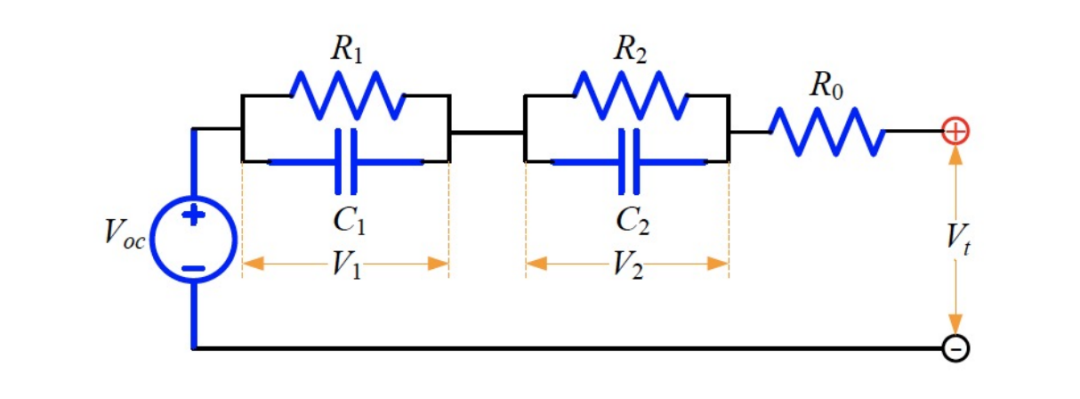
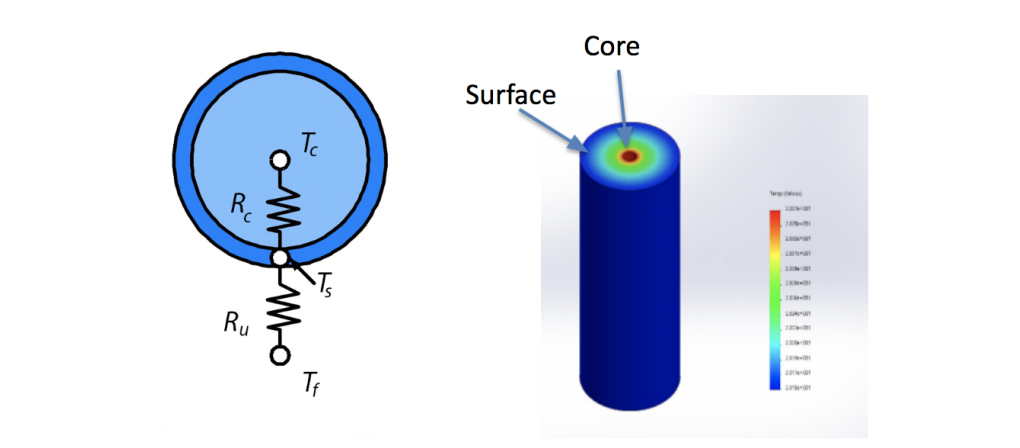
Our analysis is based on the coupled electro-thermal aging model of lithium iron phosphate batteries introduced in reference [3]. This model includes a dual RC (resistor-capacitor) pair for the electrical model, a dual-state thermal model, and a semi-empirical aging model.
For detailed article explanations, see section 4.
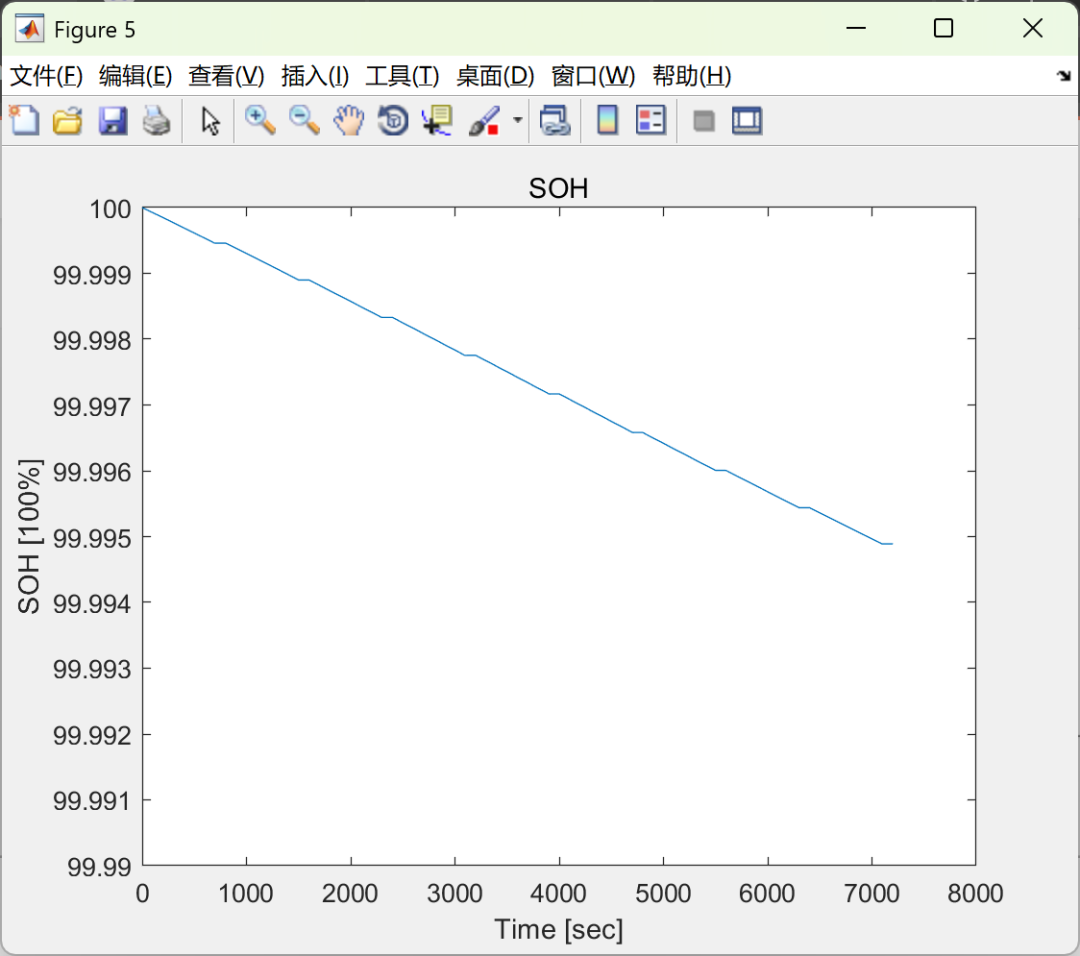
As shown in the previous section, for the temperature observer, SOC and SOH are unobservable. For the voltage observer, internal temperature (Tc), surface temperature (Ts), and SOH are unobservable. However, temperature is influenced by circuit resistance, which is also affected by temperature. Therefore, the voltage observer can indirectly “observe” Tc and Ts, as the temperature stabilizes over time. Thus, we decided to combine the temperature observer and voltage observer to form a Voltage-Temperature (VT) observer. The results indicate that the VT observer has overwhelming advantages. It can estimate most states because it combines the benefits of both the voltage observer and temperature observer. In this project, no observer can estimate SOH. However, if an accurate battery model and initial values can be provided, SOH can be well estimated through an open-loop observer.
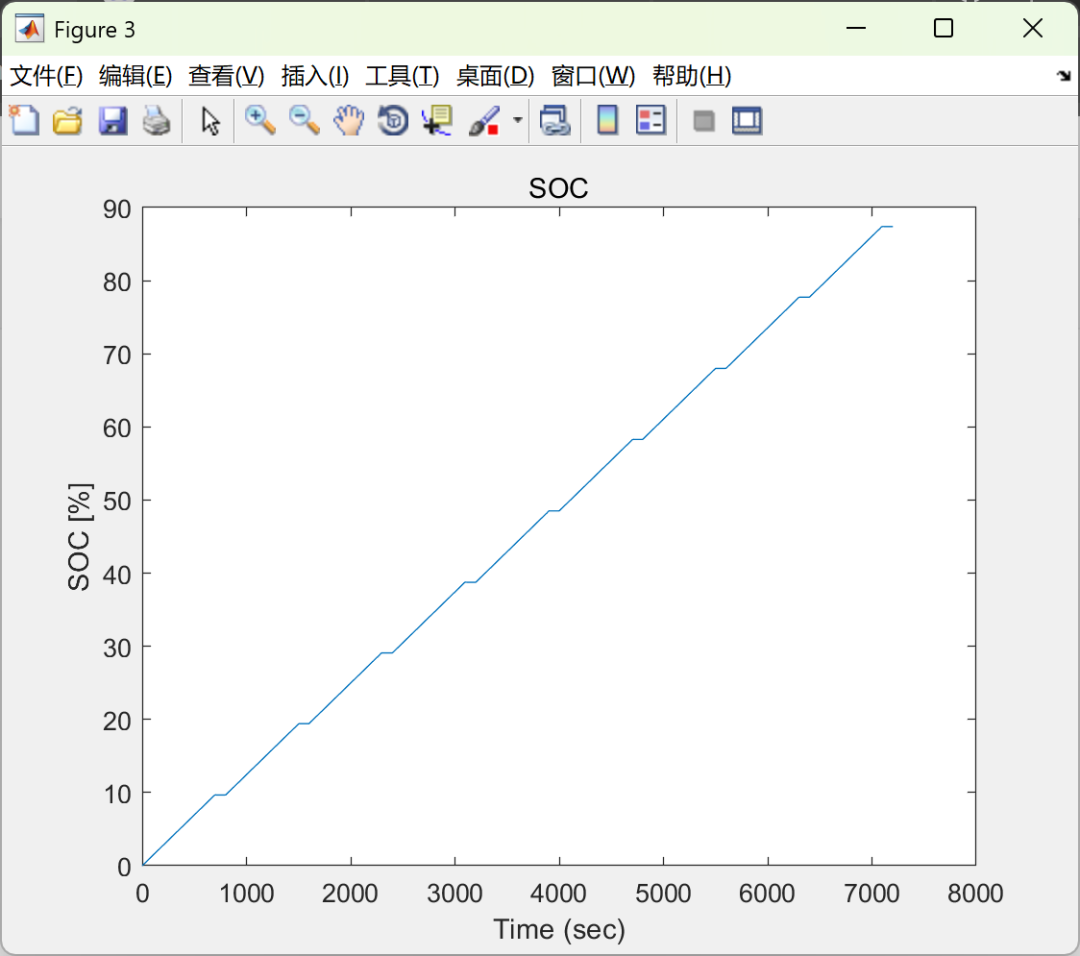
Additionally, from the simulation results, we noticed that SOC has a positive linear relationship with charging time, while SOH has a negative linear relationship with charging time. In the simulation, charging SOC from 0% to 90% takes nearly 2 hours, while SOH decreases by 0.005%. The maximum SOC is 87.4%, and the minimum SOH is 99.995%, compared to the initial state. This trend indicates a trade-off between charging time and battery health. This is interesting because it raises the issue of balancing efficiency and safety. If maximum efficiency is required, charging time should be minimized; if maximum safety is required, aging should be minimized. However, in practical applications, a balance must be found in different scenarios, leading to a new topic—optimal control of battery charging. Since batteries store most of the energy used in our daily lives, the observer we developed will serve as a useful tool to strongly support the sustainable development of energy systems. Therefore, state estimation is a very powerful tool for maintaining energy systems. In the future, a student team can focus on the optimal control of battery charging based on the observer we developed.









02

Running Results





03

Partial Code


% Create time vector(Discretized system)
DeltaT = 0.01; % Time step size [sec]
t = 0:DeltaT:(2*60*60); % Total Simulation time(hour*min*sec/min)
% Input current signals]
Current = zeros(size(t))�; % Size of Current
Current(mod(t,800) < 700) = -2.3/2; % 700sec 0.5C pulse discharge
% Current = -2.3/2 * ones(size(t))'; % 20sec 5A pulse discharge
figure
plot(t,Current)
xlabel('Time (sec)')
ylabel('Current')
title('Input')
% Iuput outside temperature
Tf = ones(size(t))';
Tf = Tf * 23.15 + sin(t'/size(t,2)*100*pi); % 20sec 5A pulse discharge
figure
plot(t,Tf)
xlabel('Time (sec)')
ylabel('Temperature')
title('Input')
input_data = [t' Current Tf];
states0 = [0;0;0; 23.15; 23.15;1];
[tsim,states] = ode45(@(t,x) ode1(t,x,input_data),t,states0);
SOC = states(:,1) * 100;
Tc = states(:,4);
Ts = states(:,5);
SOH = states(:,6) * 100;
figure
plot(t,SOC)
xlabel('Time (sec)')
ylabel('SOC [%]')
title('SOC')
figure
plot(t,Tc)
xlabel('Time (sec)')
ylabel('Temperature [0C]')
hold on
plot(t,Ts)
title('Temperature changing')
legend('core','surface')

04

References


Some content in this article is sourced from the internet, and references will be noted. If there are any inaccuracies, please feel free to contact us for removal.
[1] Liu Jianqiang, Ye Congjin, Dou Xianyun, et al. Research on State of Health Estimation of Lithium-Ion Batteries [J]. Light Industry Science and Technology, 2017(6):3.
[2] Feng Nenglian, Chen Longke, Tang Jie. Methods for Estimating the State of Health of Lithium-Ion Batteries [J]. Journal of Beijing University of Technology, 2016, 42(11):6.
[3] Jin Shuai, Dong Jing. Review of Research Progress on Data-Driven State of Health Estimation of Lithium-Ion Batteries [J]. Journal of Instrumentation, 2024, 45(3):45-59.
[4] Shi Shanshuo. Research on State of Health Estimation Method for Lithium-Ion Batteries Based on Random Charging Segments [D]. Qingdao University of Technology, 2024.





05

MATLAB Code | Article Download
