Research and Realization of the RSA Encryption Algorithm Improvement
YU Xin–hong,CHEN Qi,YAN Yu
(Economy and Technology Institute, Anhui Agricultural University, Hefei, Anhui 230011, China)
Abstract:The modular exponentiation and modular multiplication are essential elements to secure RSA algorithm. However, modular exponentiation has been so time-intensive that it impedes RSA algorithm’s application. Therefore, it is paramount to enhance the efficiency of modular exponentiation and multiplication. This paper aims to improve RSA algorithm by analyzing the principle of RSA encryption, discussing attacks against RSA algorithm, and suggesting the factors to be considered when resisting attacks.
Keywords:RSA; algorithm research; modular multiplication
0 Introduction
With the rapid development of information networks, more and more people are using the internet to share information, search for data, and conduct business transactions, making information confidentiality particularly important. The emergence of public key cryptography has played a crucial role in the development of modern cryptographic systems, and the RSA algorithm is currently one of the most widely used asymmetric encryption algorithms with relatively high security. The RSA algorithm primarily implements functions such as encryption, identity verification, and digital signatures, making it a typical public key cryptography system.
1 RSA Algorithm
1.1 RSA Encryption Algorithm
The RSA algorithm typically involves the following steps for encryption or decryption transformations.
1) Key Generation
① Select two large prime numbers p and q.
② Calculate n=pq, t=(p-1)(q-1)
(1)
where t is the Euler’s totient function of n.
③ Select an integer e such that 1<e<t, and
gcd(t,e)=1
(2)
(gcd function calculates the greatest common divisor)
④ Calculate the private key d (decryption key), such that e·d=1 mod t, where d is the multiplicative inverse of e modulo t.
⑤ Use {e,n} as the public key, and {d,n} as the private key.
2) RSA Algorithm Implementation for Encryption
Before encryption, plaintext should be grouped such that each group is less than n, which means the binary length of each group is less than log2n. Then, for each plaintext group m, perform the encryption operation [1]:
C=me mod n
(3)
3) RSA Algorithm Implementation for Decryption
The decryption operation for the ciphertext groups obtained is:
m=cd mod n
(4)
1.2 RSA Signature Algorithm
Generally, if a public key system is used as a cryptographic system, it cannot simultaneously serve as a digital signature, and vice versa. Only a few encryption systems can be used for both cryptography and digital signatures [2], and the RSA algorithm discussed in this paper is one of them. The RSA signature algorithm is as follows:
Let n=pq, where p and q are two large prime numbers [3], and e and d satisfy
ed=1(mod t).
(5)
Public Key: n, e
Private Key: d
For signing: Y=Xd mod n; and send the encrypted information and signature Y to the receiver;
For verification: the receiver uses the sender’s public key e to verify the received message y by performing the digital signature verification transformation X′=ye mod n [1], and uses the sender’s private key to decrypt the received information. If X′=X, it confirms the legitimacy of the sender’s identity.
The above process can basically realize the digital signature function of the RSA algorithm, but it is crucial that the user must first make their public key public so that other users can verify their signature; otherwise, other users cannot verify its correctness.
Through the analysis of the RSA algorithm, this paper will improve the RSA algorithm by selecting parameters and explaining the conditions for implementing the RSA algorithm, as well as the specific implementation process.
2 RSA Parameter Selection
According to the encryption and decryption process of the RSA algorithm, there are three main parameters involved: modulus n, encryption key e, and decryption key d.
2.1 Selection of n
In the RSA algorithm, n is the product of p and q, which is then used to generate the key pair. The factorization of modulus n is the most direct attack method; if n is factored, the information will be compromised [4]. Therefore, the selection of modulus n is very important, and generally, n must satisfy the following conditions:
1) The difference between p and q should be large.
However, if p and q are chosen to be very close, given n, one can assume the average of the two as (p+q)/2 is approximately n/2, and then use ((p+q)/2)2–n=((p–q)/2)2. If the right side can be square-rooted, then (p+q)/2 and (p–q)/2 can be obtained, meaning n has been factored [6].
2) The greatest common divisor of p-1 and q-1 should be small.
3) p and q must be strong primes.
A prime p is considered strong if there exist two large primes p1, p2 such that both p1/p-1 and p2/p+1 hold true, or if there exist four large primes r1, r2, s1, s2 such that r1/p1-1, s1/p1+1, r2/p2-1, s2/p2+1 all hold true. Only when n is the product of two strong primes is its factorization a mathematically challenging problem.
4) p and q should be large enough to make factorization of n computationally infeasible.
The RSA algorithm primarily relies on the factorization of large numbers for its security. If modulus n can be factored, it effectively compromises the algorithm. Thus, the selection of modulus n must be sufficiently large to ensure that its factorization is computationally infeasible [5]. The factorization problem is one of the most common challenges in cryptography. Although significant progress has been made in factorization algorithms, there is still insufficient evidence to prove that RSA can be broken. To ensure adequate security for the RSA algorithm, the primes p and q should be at least 300 bits long, resulting in a modulus n of over 600 bits [5]. Currently, most entities use 1024-bit keys, and as computational power increases, the length of secure keys also grows.
2.2 Selection of e
The condition that e and t are coprime is relatively easy to satisfy. If a small e is chosen, it speeds up the encryption and decryption calculations and is easier to store, but it also reduces security.
Generally, the selection principles for e are as follows:
1) e should not be chosen too small. In the RSA algorithm, as long as the public key e satisfies gcd (e, t)=1, e can be selected arbitrarily. To reduce computation time, many people choose a relatively small value for e [6], but a low exponent significantly lowers the overall security of the algorithm. Therefore, e is generally chosen to be a 16-bit prime to effectively prevent security attacks while also maintaining a fast computation speed.
2) e should have the maximum order in mod t. That is, there exists an i such that
ei=1(mod t)
(6)
where i is greater than (p-1)(q-1)/2, which can effectively resist attacks.
2.3 Principles for Selecting d
The private key d cannot be too small, generally at least greater than n/4. This is because if d is too short, it may be possible to guess d using known plaintext m after encryption to obtain c=me mod n, and then directly check if cd mod n equals m. If it does, then d is the decryption key; if not, continue guessing. If d is too short, the guessing range is small, and the probability of guessing correctly is high. For these reasons, d should not be too short.
3 Implementation of the RSA Algorithm
3.1 Prime Generation
Probabilistic tests are typically used for primality testing (the results may not be 100% accurate), but the accuracy of the test increases with the number of times the number is tested. Common verification methods include Fermat’s primality test, Miller-Rabin test, Solovay-Strassen test, and Lucas-Lehmer test, with the last three being based on Fermat’s test.
In common algorithms for generating primes, a large integer is generated first, followed by a primality test to determine if it is prime [6]. If it fails the test, it is incremented by 2 and tested again until it passes. Some special forms of strong primes can prevent simple attack methods, but they require a lot of time. Therefore, choosing a sufficiently large prime is more important for the RSA algorithm.
3.2 Key Generation
The RSA algorithm belongs to the public key cryptography system and has a pair of keys (public and private key). Randomly select an encryption key e and determine if it is coprime with t.
The method for determining if two numbers are coprime is to first check if the greatest common divisor (using the gcd function) is 1; if so, the two numbers are coprime. According to the Euclidean algorithm, if a=bn+c, then gcd(a,b)=gcd(b,c), so we can repeatedly calculate the remainder and the original divisor, and the final non-zero remainder will be the greatest common divisor.
The public key generation process is illustrated in Figure 1.
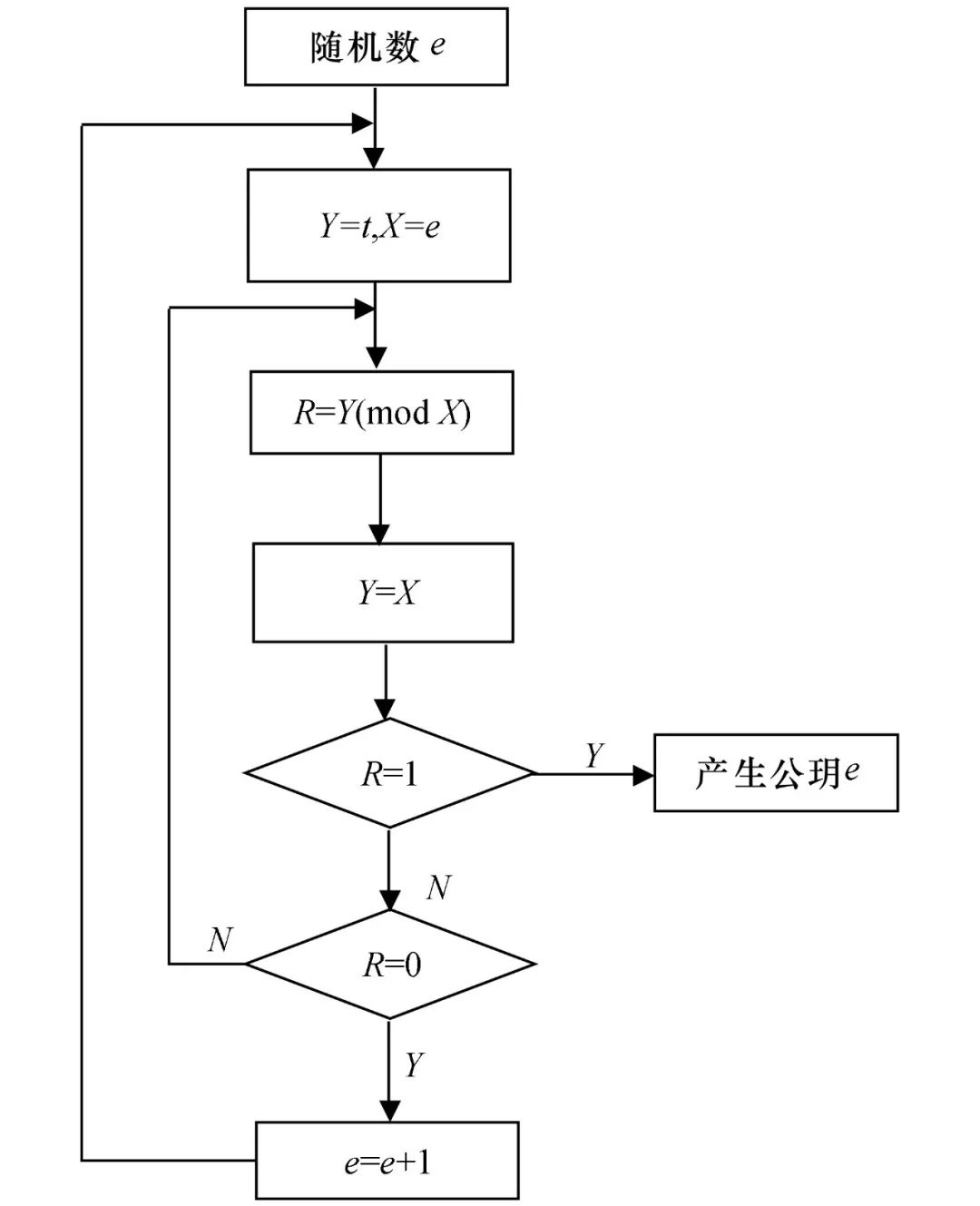
Figure 1 Public Key Flow Chart
After obtaining the encryption key through the above process, the decryption key d can be calculated using the formula e·d=1 mod t.
3.3 SMM Modular Multiplication Algorithm
The core of the RSA algorithm is modular multiplication, as most operations in RSA are modular exponentiation, which can be transformed into modular squaring and multiplication. For the improvement of the RSA algorithm, this paper employs the SMM algorithm primarily based on the “multiplicative congruence symmetry property” to reduce the base for each operation, thereby decreasing the time of modular multiplication and increasing computational speed.
In the RSA algorithm, n is the product of two large primes, thus n must be odd, and both n-1 and n+1 must be even. Therefore, (n-1)/2 and (n+1)/2 must be integers [6]. According to the properties of modular arithmetic, (n–i)(n–j)=n2–ni–nj+ij=ij(mod n) (i,j∈{0,1,2,…,(n-1)/2,(n+1)/2,…,n-1}). In the modular exponentiation of the RSA algorithm, larger numbers can be transformed into smaller numbers for modular squaring and multiplication, thus speeding up the computation.
3.4 Specific Implementation of RSA Algorithm Improvement
The formulas and functions used in the implementation process include:
① To determine if two numbers are coprime, the greatest common divisor must be 1, which can be achieved using the gcd function.
② Modular arithmetic refers to the remainder operation,
a=b(mod n)⟺a=b%n
(7)
③ The calculation formula for the modular inverse b of a number a is
ab=1 mod n
(8)
According to the Euclidean algorithm, this is equivalent to calculating ab=n*k+1 (k is a natural integer), and finding suitable k and b is sufficient.
First, two random large primes p and q (kept secret) are selected, then n=p*q, t=(p-1)(q-1) is calculated. Based on the previous mention of gcd(t,e)=1 and Figure 1, the public key e (public) is generated. Then, e·d=1 mod t is used to calculate the private key d (private). {e,n} is the public key, and {d,n} is the private key. For each plaintext group m, the encryption algorithm is applied: c=me mod n, while for each ciphertext group c, the decryption algorithm is: m=cd mod n.
The main program results of the RSA algorithm are shown in Figures 2 and 3.
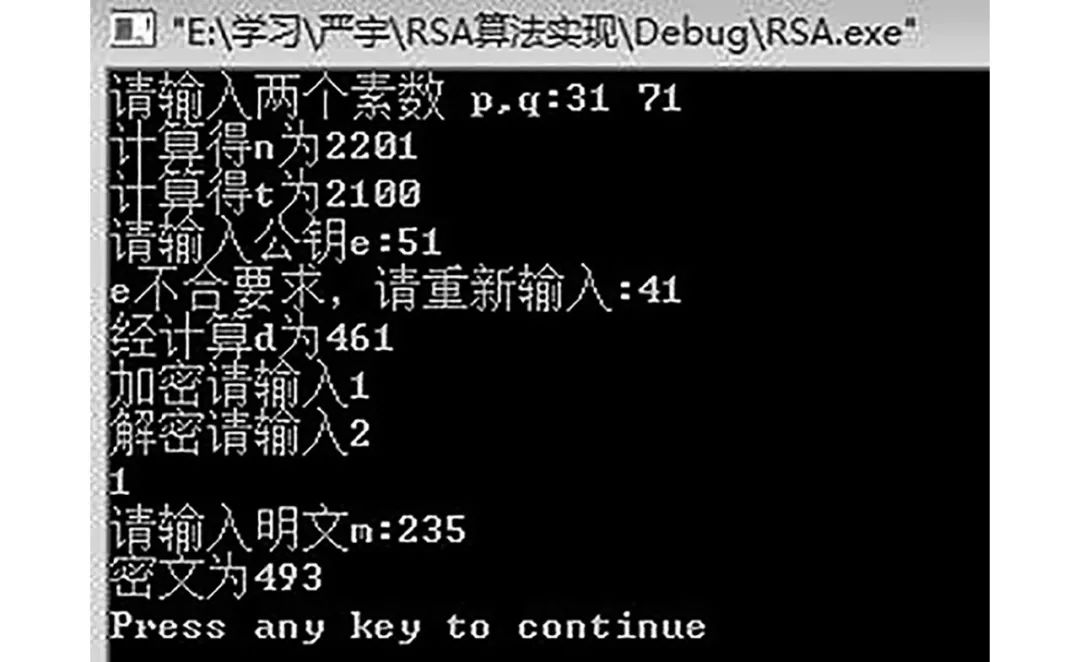
Figure 2 Encryption Operation Result
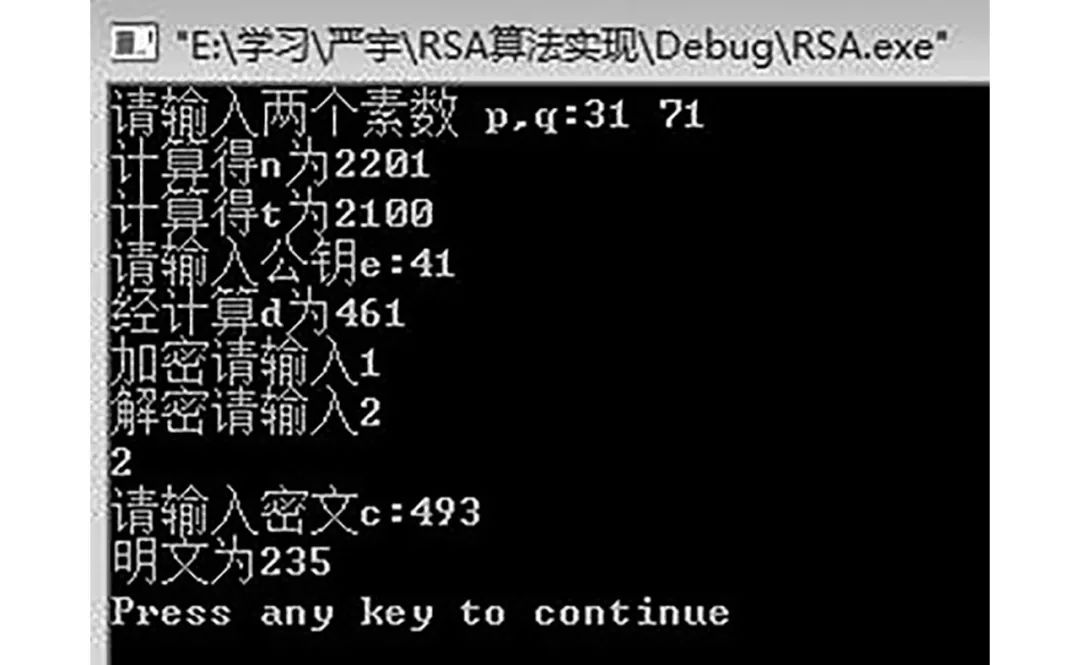
Figure 3 Decryption Operation Result
4 Result Analysis and Explanation
By comparing Figures 2 and 3, it can be seen that before the improvement of the RSA algorithm, the program’s running results indicated that the first randomly selected e did not meet the rules, and the correction function for the public key could not be implemented. Following the RSA encryption algorithm improvement process mentioned above, the choices for encryption or decryption and the outputs of plaintext and ciphertext results further verify the correctness of the RSA algorithm improvement.