
The password mentioned here is not the same concept as the passwords we usually use.
This article discusses encryption algorithms that primarily solve the problem of encryption and decryption in information transmission. It assumes that the data transmission process is insecure, and all information is being eavesdropped on, so the sender must encrypt the information, and the receiver must know how to decrypt it after receiving the information.
Interestingly, if you can let the receiver know how to decrypt, can’t the eavesdropper also know how to decrypt?
Therefore, cryptography is quite magical. When I first saw the Diffie-Hellman key exchange algorithm, I was amazed: two people can exchange a few numbers in front of you, and they can have a common secret; you know these numbers and the specific steps of the algorithm they are using, but you can never calculate this secret.
Below, we will introduce symmetric encryption algorithms, the Diffie-Hellman key exchange algorithm, asymmetric encryption algorithms, digital signatures, and public key certificates to see the bumpy road of solving secure transmission problems.
1. Symmetric Encryption
Symmetric encryption, also known as shared key encryption, uses the same key for encryption and decryption.
For example, let me describe the simplest method of symmetric encryption. First, we know that information can be represented as a sequence of 0/1 bits, and we know that the result of XORing two identical bit sequences is 0.
So we can generate a random bit sequence of the same length as the original information as the key, and then use it to XOR the original information to generate the ciphertext. Conversely, XORing the ciphertext with the same key will restore the original information.
This is a simple example, but it is too simple and has many issues. For instance, the length of the key is exactly the same as the original information; if the original information is large, the key will also be equally large, and generating a large number of truly random bit sequences has significant computational overhead.
Of course, there are many more complex and efficient symmetric encryption algorithms that solve these problems, such as the Rijndael algorithm and Triple DES algorithm.They are algorithmically impeccable, meaning they have a vast key space that is practically impossible to brute-force, and the encryption process is relatively fast.
However, the Achilles’ heel of all symmetric encryption algorithms lies in key distribution. The same key is used for both encryption and decryption, and the sender must find a way to send the key to the receiver. If the eavesdropper can steal the ciphertext, they can also steal the key, making even the most flawless algorithm vulnerable.
Therefore, we will introduce two of the most common algorithms to solve the key distribution problem, namely the Diffie-Hellman key exchange algorithm and asymmetric encryption algorithms.
2. Key Exchange Algorithm
The key we are talking about is generally a large number, which the algorithm uses for encryption and decryption. The problem is that the channel is insecure, and all data sent can be intercepted. In other words, is there a way for two people to openly exchange a secret in front of everyone, securely sending the symmetric key to the receiver?
The Diffie-Hellman key exchange algorithm can achieve this.To be precise, this algorithm does not securely “send” a secret to the other party but generates a common secret in each party’s “mind” through some shared numbers, and this secret cannot be generated by a third-party eavesdropper.
Perhaps this is what is known as a mutual understanding.
The rules of this algorithm are not complicated; you can even try to share a secret with a friend, and I will briefly outline its basic process later. Before that, it is essential to clarify one issue:not all operations have inverse operations.
The simplest example is the well-known one-way hash function, where given a number<span>a</span> and a hash function<span>f</span>, you can quickly calculate<span>f(a)</span>, but if you are given<span>f(a)</span> and<span>f</span>, deducing<span>a</span> is practically impossible. The reason the key exchange algorithm seems so magical is that it utilizes this irreversible nature.
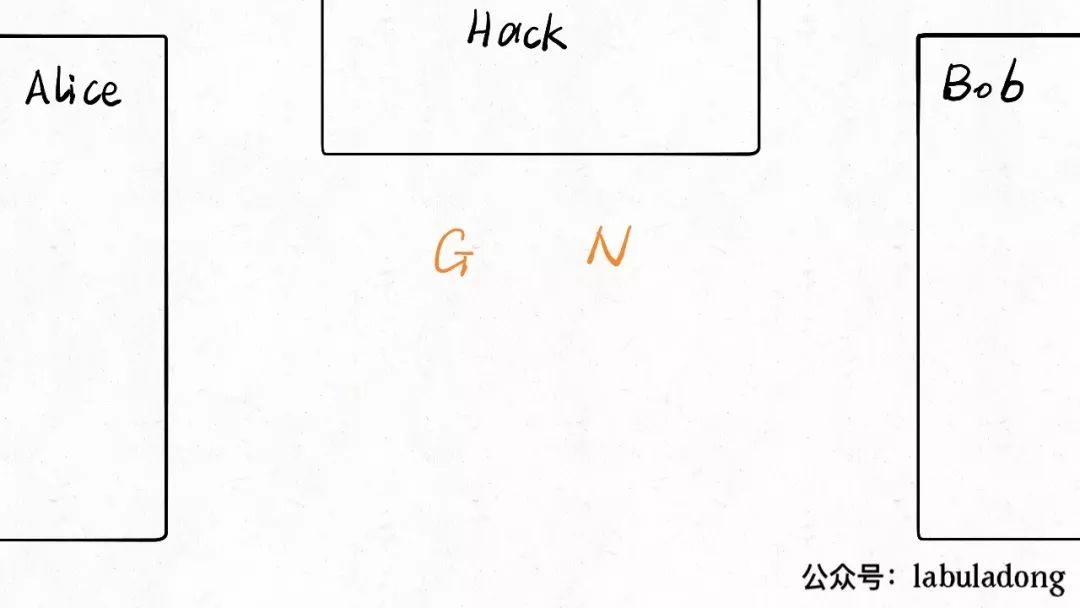
Now, let’s look at the process of the key exchange algorithm. According to naming conventions, the two parties preparing to execute the key exchange algorithm are called Alice and Bob, while the bad actor attempting to intercept their communication is called Hack.
First, Alice and Bob agree on two numbers<span>N</span> and<span>G</span> as generators. Of course, the negotiation process can be overheard by the eavesdropper Hack, so I will depict these two numbers in the middle, indicating that all three parties know:
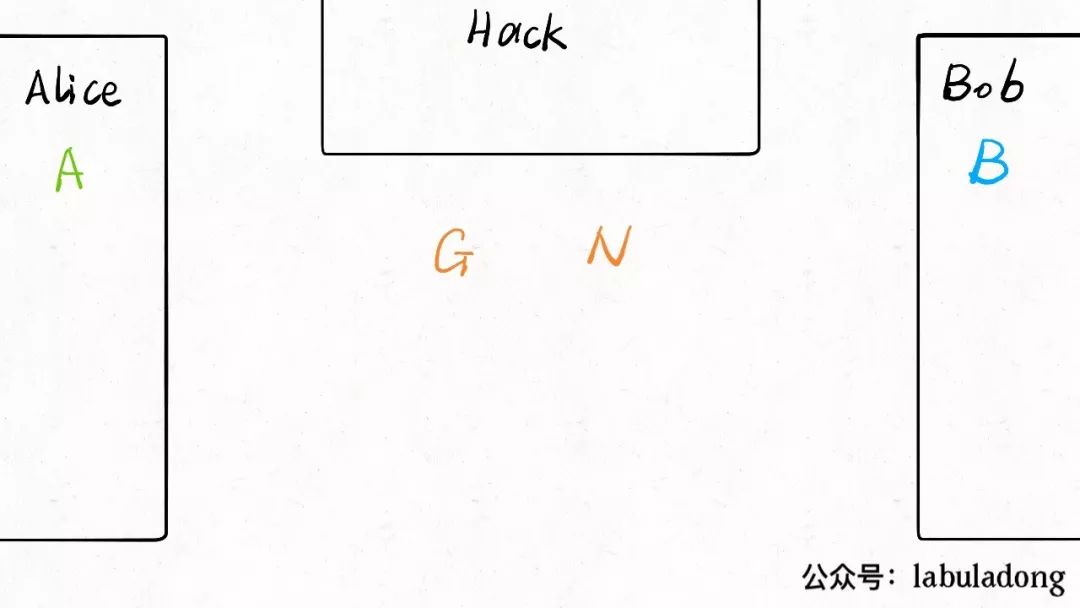
Now Alice and Bob each think of a number, called<span>A</span> and<span>B</span> respectively:
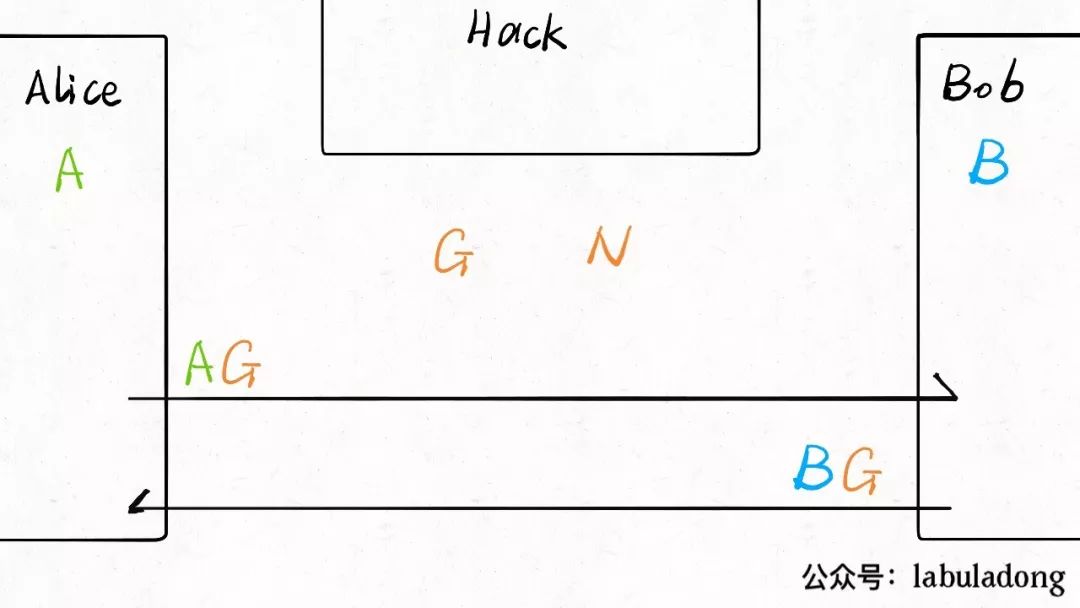
Now Alice takes her number<span>A</span> and<span>G</span> to derive a number<span>AG</span>, then sends it to Bob; Bob takes his number<span>B</span> and<span>G</span> to derive a number<span>BG</span>, then sends it to Alice:
The situation now becomes:
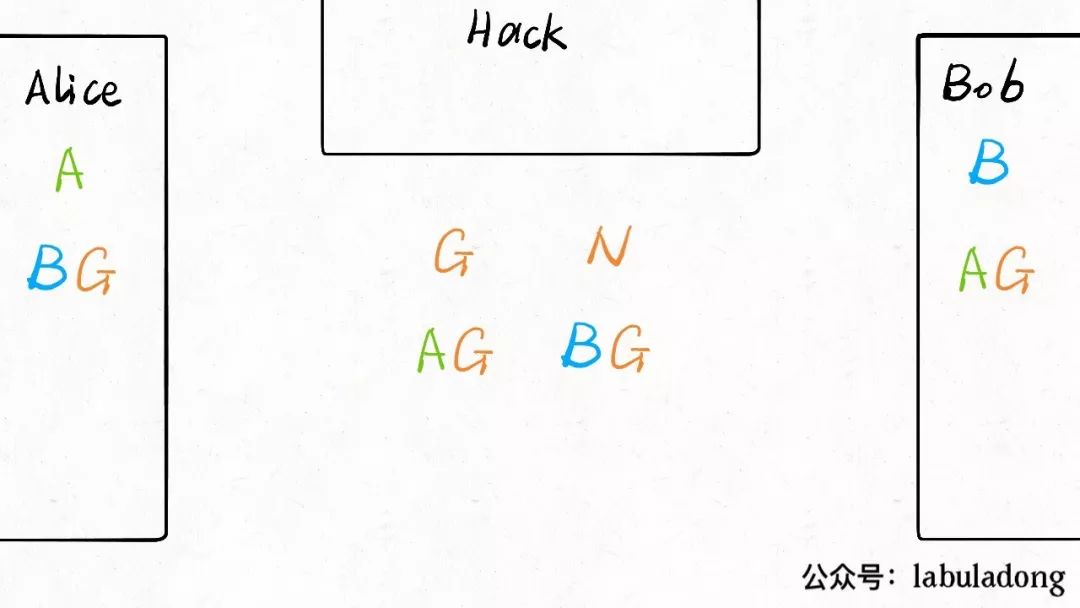
Note that, similar to the hash function example mentioned earlier, knowingAG and G does not allow one to deduce A, and BG is similar.
PS: The specific operations involve modular (mod) and exponentiation; the reason it cannot be inverted is that mathematicians have yet to find a fast algorithm for discrete logarithms.
Then, Alice can derive a number<span>ABG</span> using<span>BG</span> and her<span>A</span> through some operations, and Bob can also derive<span>ABG</span> using<span>AG</span> and his<span>B</span>; this number is the shared secret between Alice and Bob.
As for Hack, they can intercept<span>G</span>,<span>AG</span>, and<span>BG</span>, but due to the irreversible calculations, they cannot combine these to derive<span>ABG</span><code><span>:</span>
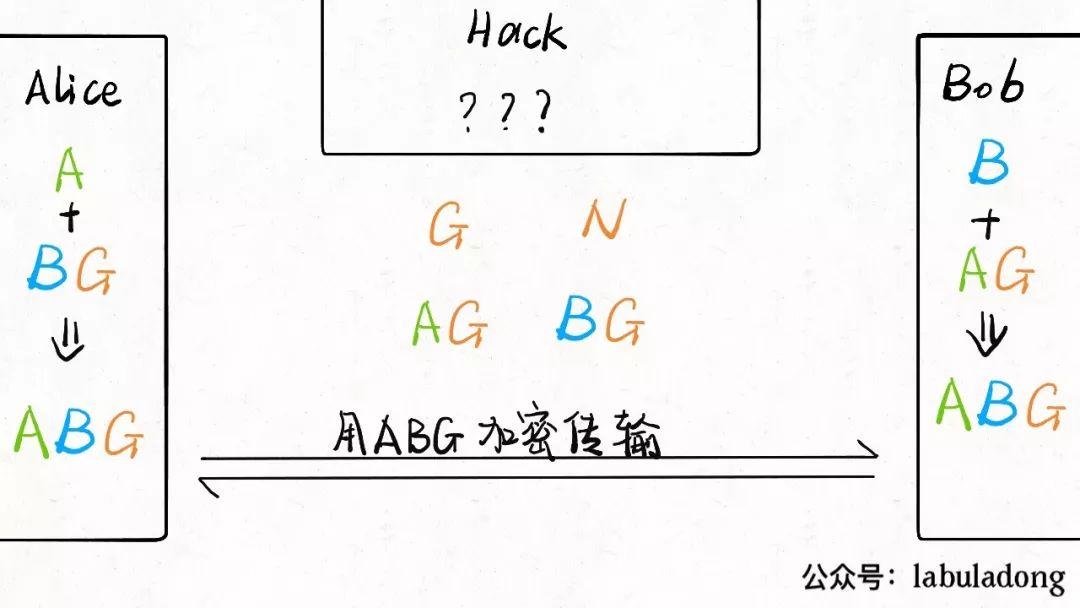
PS: In the specific algorithm, N is used for modular arithmetic, so it is omitted in the diagram.
That is the basic process. As for the specific values of the numbers, there are nuances, and the specific calculation methods can be easily found on Baidu; I won’t go into detail here due to space constraints.
This algorithm can calculate a secret that others cannot compute as the key for symmetric encryption algorithms, allowing for symmetric encrypted communication to commence.
For this algorithm, Hack has thought of a way to crack it, not by eavesdropping on Alice and Bob’s communication data, but by impersonating both Alice and Bob simultaneously, which is what we call a man-in-the-middle attack:
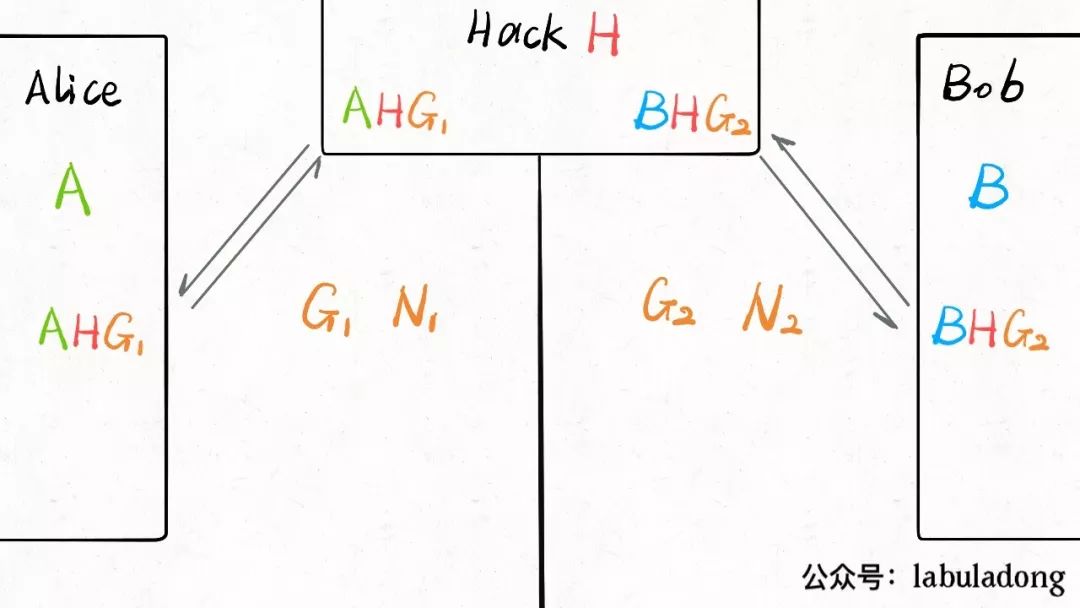
In this case, both parties cannot detect that they are sharing secrets with Hack, resulting in Hack being able to decrypt or even modify the data.
Clearly, the key exchange algorithm does not completely solve the key distribution problem, as it cannot verify the identity of the other party. Therefore, before executing the key exchange algorithm, it is generally necessary to verify the identity of the other party, such as using digital signatures.
3. Asymmetric Encryption
The idea of asymmetric encryption is to simply not transmit the key secretly; instead, I separate the encryption key and the decryption key, using the public key for encryption and the private key for decryption. I only send the public key to the other party, and then the other party starts sending me encrypted data, which I can decrypt with my private key. As for the eavesdropper, having the public key and the encrypted data is useless, as only my private key can decrypt it.
One can think of it this way: the private key is the key, while the public key is the lock; I can publicly share the lock so that others can lock the data and send it to me; however, the key must remain with me for unlocking. The commonly known RSA algorithm is a typical asymmetric encryption algorithm, and its specific implementation is quite complex; I won’t write it here as there is a lot of information available online.
In practical applications, the computational speed of asymmetric encryption is significantly slower than that of symmetric encryption, so when transmitting large amounts of data, the public key is generally not used to encrypt the data directly; instead, the symmetric encryption key is encrypted and sent to the other party, after which both parties use symmetric encryption algorithms to transmit data.
It is essential to note that, similar to the Diffie-Hellman algorithm, asymmetric encryption algorithms also cannot verify the identities of the communicating parties and are still susceptible to man-in-the-middle attacks. For instance, if Hack intercepts the public key sent by Bob and impersonates Bob’s identity to send Alice their public key, then Alice, unaware, will encrypt sensitive data using Hack’s public key, allowing Hack to decrypt and steal it using their private key.
So, both the Diffie-Hellman algorithm and the RSA asymmetric encryption algorithm can solve the key distribution problem to some extent, but they share the same flaws. What are the differences in their application scenarios?
Simply put, the basic principles of the two algorithms clarify this:
If both parties have a symmetric encryption scheme and wish to encrypt communication without letting others obtain the key, they can use the Diffie-Hellman algorithm to exchange keys.
If you want anyone to encrypt information while only you can decrypt it, then use the RSA asymmetric encryption algorithm and publish the public key.
Next, let’s try to solve the problem of authenticating the sender’s identity.
4. Digital Signatures
As mentioned earlier, asymmetric encryption allows the public key to be publicly used for others to encrypt data sent to you, which can only be decrypted with your corresponding private key. In fact, the private key can also be used to encrypt data; for the RSA algorithm, the data encrypted with the private key can only be decrypted with the public key.
Digital signatures also utilize the properties of asymmetric keys but are completely reversed from public key encryption: the public key is still published, but you encrypt the data with your private key and then publish the encrypted data; this is the digital signature.
You might ask, what is the use of this? The public key can decrypt the data encrypted with the private key, so why encrypt and send it out? Isn’t that redundant?
Yes, but the purpose of the digital signature is not to ensure the confidentiality of the data but to prove your identity, to show that this data was indeed sent by you.
Think about it: if the data encrypted with your private key can only be decrypted with your public key, then if an encrypted piece of data can be decrypted by your public key, it proves that this data was sent by you (the holder of the private key).
Of course, the encrypted data is merely a signature; the signature should be sent along with the data. The specific process should be:
1. Bob generates a public key and a private key, then publishes the public key while keeping the private key.
2. Encrypt the data with the private key as a signature, then publish the data along with the signature.
3., Alice receives the data and signature and needs to verify whether the data was sent by Bob. She attempts to decrypt the signature using the public key previously sent by Bob, comparing the received data with the result after decrypting the signature. If they are identical, it indicates that the data has not been tampered with and was indeed sent by Bob.
Why is Alice so sure? After all, both the data and the signature can be swapped out, right? The reasons are as follows:
1. If someone modifies the data, Alice will find a discrepancy when she decrypts the signature and compares the two.
2. If someone replaces the signature, Alice can only decrypt a garbled string using Bob’s public key, which is evidently inconsistent with the data.
3. Perhaps someone attempts to modify the data and create a signature for the modified data, making it impossible for Alice to detect the inconsistency upon comparison; however, once the signature is decrypted, it is impossible to regenerate Bob’s signature because the private key is not available.
In summary, digital signatures can authenticate the source of the data to a certain extent. The reason it is said to be to a certain extent is that this method is still vulnerable to man-in-the-middle attacks. Once the public key is involved in its release, the receiver may receive a fake public key from the man-in-the-middle, leading to incorrect authentication, and this issue cannot be completely avoided.
Ironically, digital signatures are a means of verifying the identity of the other party, but the premise is that the identity of the other party must be genuine… This seems to fall into a paradox of whether the chicken or the egg came first, to determine the identity of the other party, there must be a trusted source; otherwise, no matter how many processes are involved, it merely shifts the problem rather than truly resolving it.
5. Public Key Certificates
A certificate is essentially a public key + signature issued by a third-party certification authority. Introducing a trusted third party is a feasible solution to end the trust loop.
The certification process is roughly as follows:
1. Bob goes to a trusted certification authority to verify his true identity and provides his public key.
2. Alice wants to communicate with Bob, first requesting Bob’s public key from the certification authority, which sends a certificate (Bob’s public key and the institution’s signature on it) to Alice.
3. Alice checks the signature to confirm that the public key was indeed sent by the certification authority and has not been tampered with.
4.Alice encrypts data using this public key and starts communicating with Bob.
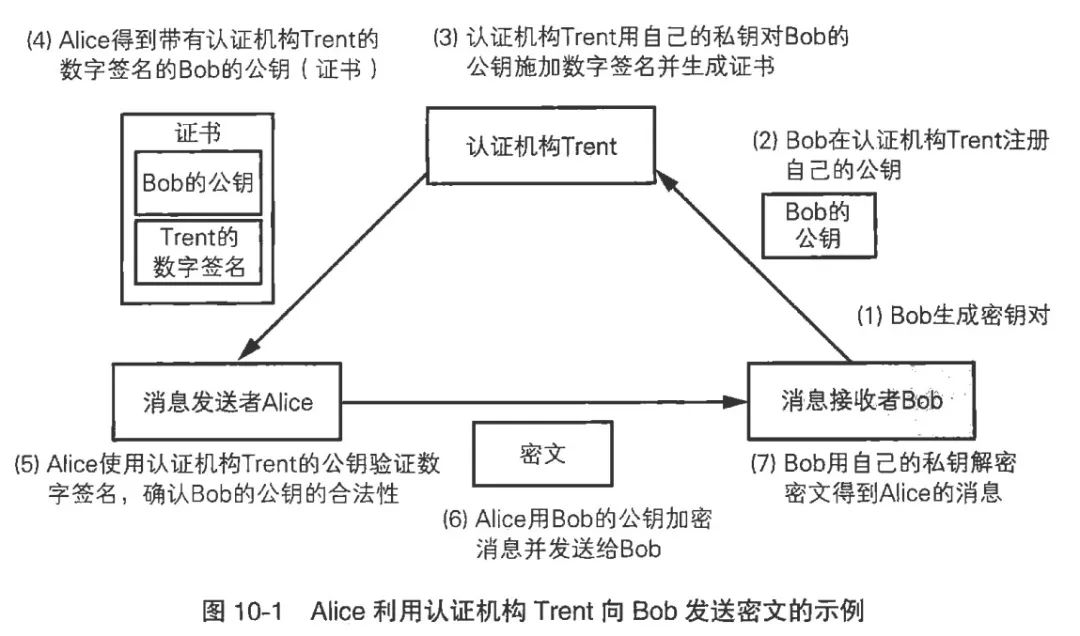
PS: The above image is for illustration; in reality, a certificate only needs to be installed once and does not require a request to the certification authority every time; generally, the server directly sends the certificate to the client instead of the certification authority.
Some may ask, for Alice to determine the validity of the certificate through the digital signature, she must have the (certification) public key of the authority, doesn’t that lead back to the earlier trust loop?
All the legitimate browsers we install have pre-stored certificates of legitimate certification authorities (including their public keys) to confirm the identity of the authority, which makes the certification of certificates trustworthy.
During the process of Bob providing his public key to the authority, he must provide a lot of personal information for identity verification, which is quite strict, so it is considered reliable.
Having obtained Bob’s trusted public key, the communication between Alice and Bob is protected by encryption algorithms, making it completely flawless.
In summary, each side of this triangle is relatively reliable, making it costly for hackers to launch attacks.
Most legitimate websites now use the HTTPS protocol, which adds an SSL/TLS security layer between the HTTP protocol and the TCP protocol. After your browser and the website server complete the TCP handshake, the SSL protocol layer also performs an SSL handshake to exchange security parameters, which includes the website’s certificate for the browser to verify the site’s identity. Once the SSL security layer verification is complete, the content of the upper-layer HTTP protocol will be encrypted, ensuring the secure transmission of data.
As a result, traditional man-in-the-middle attacks have almost no survival space; the attack methods can only shift from technical flaws to deceit. In fact, deceit can be more efficient; for example, I have found many download websites that publish browsers that not only contain various navigation and bookmark URLs but also include some non-legitimate certification authority certificates. Anyone can apply for a certificate, and these illegitimate certificates can pose security risks.
6. Final Summary
Symmetric encryption algorithms use the same key for both encryption and decryption, making them hard to crack and fast in encryption speed, but they have key distribution issues.
The Diffie-Hellman key exchange algorithm allows both parties to achieve a mutual understanding, solving the key distribution problem to some extent, but it cannot verify the identities of the communicating parties, making it susceptible to man-in-the-middle attacks.
Asymmetric encryption algorithms generate a pair of keys, separating the tasks of encryption and decryption.
The RSA algorithm, as a classic asymmetric encryption algorithm, has two purposes: if used for encryption, it can publish the public key for encryption, with only the private key being able to decrypt, ensuring data confidentiality; if used for digital signatures, after publishing the public key, the private key can encrypt data as a signature to prove that the data was sent by the private key holder. However, regardless of the usage, involving the release of the public key cannot avoid man-in-the-middle attacks.
A public key certificate consists of a public key + signature, issued by a trusted third-party certification authority. Since legitimate browsers come pre-installed with the public keys of trusted certification authorities, they can effectively prevent man-in-the-middle attacks.
The SSL/TLS security layer in the HTTPS protocol combines the above encryption methods, so do not install non-legitimate browsers, and avoid installing certificates from unknown sources.
Cryptography is just a small part of security; even a HTTPS site certified by a legitimate authority does not imply trustworthiness; it only means that its data transmission is secure. Technology can never truly protect you; the most important thing is to enhance personal security awareness, stay vigilant, and handle sensitive data cautiously.
Finally, if you find this article well-written, give it a look and share it; if the data is good, I will write more.
END
● Learn "Backtracking Search Algorithm" Problem Solving Skills
● How to Use Winter Vacation Time to Prepare for the 2020 Blue Bridge Cup?
● A Slice of Bread to Help You Understand the Importance of Handwashing
● Data Structure and Algorithm Learning Guide
Click "Look" to understand