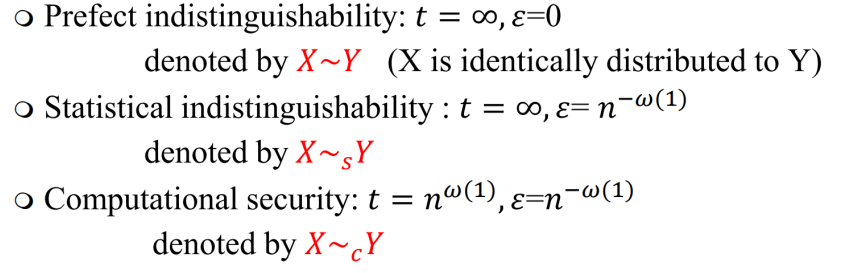Abstract:This article is the course notes from Professor Yu Yu’s summer class on homomorphic encryption. Professor Yu is a professor in the Department of Computer Science and Engineering at Shanghai Jiao Tong University, mainly engaged in research related to cryptography. The course first introduces some basic concepts of cryptography, and then discusses some fundamental theories of homomorphic encryption.
Encryption Schemes and Security Concepts
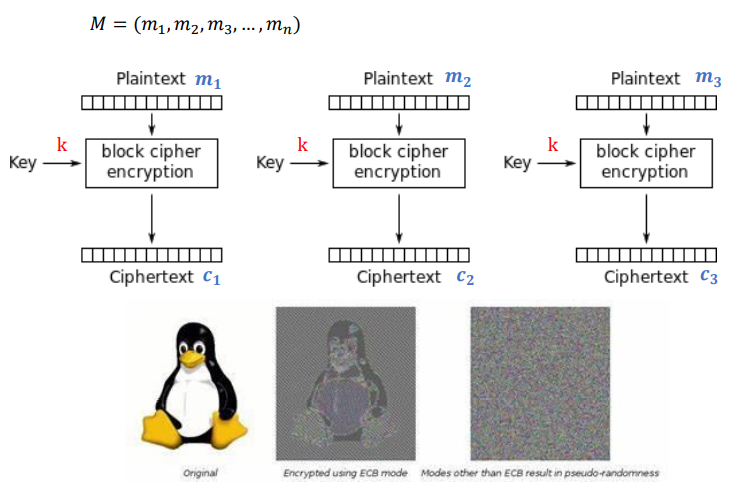
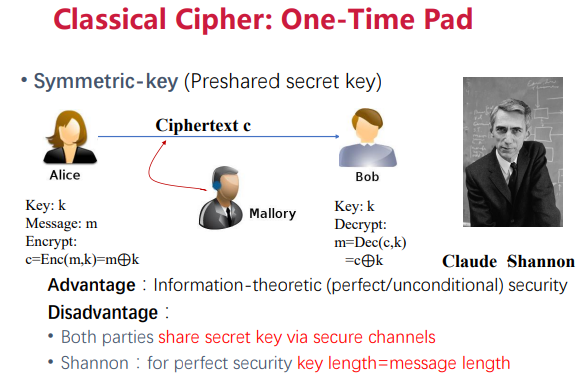
1.1 Classic Encryption: One-Time Pad
This is symmetric encryption, where both sides share a symmetric key. Advantages: Information-theoretic security, meaning the mutual information between c and m is 0. Disadvantages: Low efficiency, requires a secure channel to share the key; to achieve perfect security, the message and key must be of the same length.
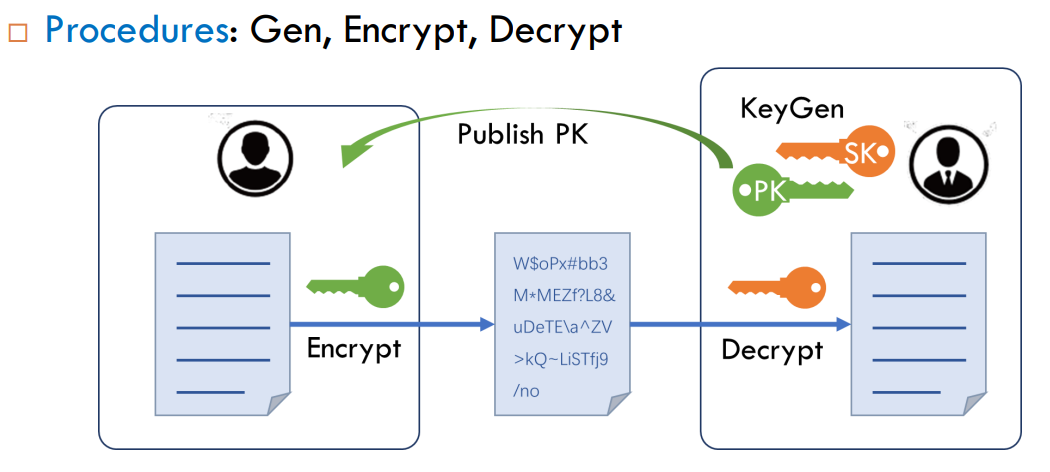
1.2 Public-key Encryption
Asymmetric encryption consists of three processes: key generation algorithm, encryption algorithm, decryption algorithm.

Chosen Plaintext Attack and Chosen Ciphertext Attack
Chosen Plaintext Attack (CPA) refers to an adversary choosing plaintext and obtaining the corresponding ciphertext. Chosen Ciphertext Attack (CCA) means the adversary can not only choose plaintext to obtain ciphertext, but can also choose a limited number of ciphertexts to obtain the corresponding plaintext. CCA describes a stronger capability of the adversary than CPA.
CPA security. We describe chosen plaintext attack (CPA) as a game for better understanding. First, it should be stated that the purpose of this game is to break the system’s indistinguishability (Indistinguishability) under the premise of chosen plaintext attack, so we will refer to this game as IND-CPA. Furthermore, we need to define two roles: challenger C and adversary A. The challenger’s task is akin to that of a referee, hosting the game and providing feedback on the adversary’s actions. The adversary, as the name suggests, is the one attacking the current system, and for this game, attacks using the method of chosen plaintext attack. The game is described as follows:
A. Initialization: Challenger C creates the IND-CPA system and sends the public key to adversary A.
B. Adversary A chooses two plaintexts m0 and m1 of the same length and sends them to challenger C. Challenger C randomly selects b∈{0,1} and encrypts mb, recording it as cb, and then sends ciphertext cb to adversary A.
C. Adversary A guesses whether the plaintext encrypted by challenger C in the previous step was m0 or m1, and outputs the guess result, noted as . If , then the adversary’s attack is successful.
Deterministic Encryption is Non-Semantically Secure
Deterministic encryption scheme: The encryption scheme is deterministic, where each plaintext corresponds to one ciphertext. The adversary can easily compare the re-encrypted message with the target ciphertext during indistinguishability attacks. For example, RSA encryption.
Probabilistic encryption scheme: A random number is chosen for each encryption, generating different ciphertexts for the same plaintext. For example, ElGamal encryption.
In the presence of an eavesdropper, CPA security and indistinguishable encryption are equivalent. No deterministic encryption scheme is CPA secure; in the presence of an eavesdropper, there is no deterministic public key encryption scheme that possesses indistinguishable encryption.
For two distributions X and Y, we define them as -indistinguishable if for any time t:
We define perfect indistinguishability, statistical indistinguishability, and computational security as follows:
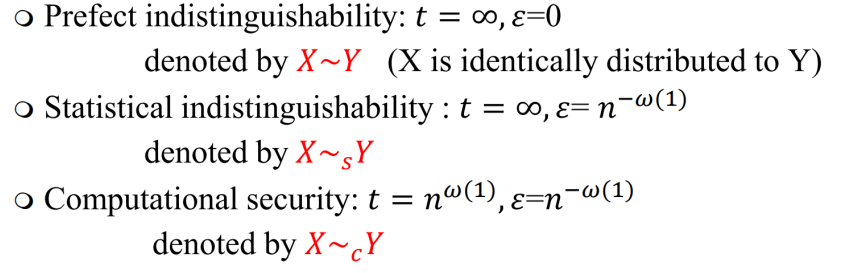
2.2 Statistical Distance
The statistical distance commonly used in cryptography is defined as follows:

2.3 Hash Functions
Let U be the universe of keys, and H is a finite set of hash functions. The hash functions in H map U to the slots of the hash table 0, 1, …, m-1. If the condition holds, we say H is universal. The left side of the equation indicates the number of hash functions that map x and y to the same slot. Thus, if a hash function is randomly chosen from H, the probability of x and y colliding is 1/m.
For, there are t+d bits of min-entropy, where A is randomly chosen, and has length t, taking values from {0,1} uniformly distributed.
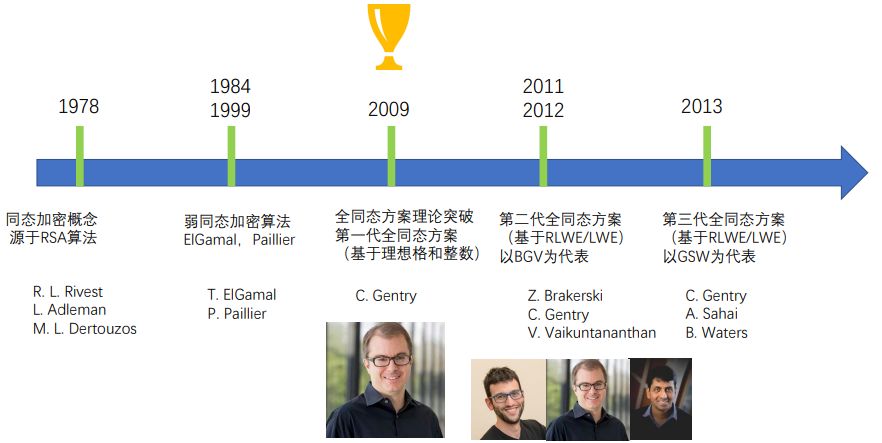
3.1 Development of (Fully) Homomorphic Encryption Algorithm Theory
Types of Homomorphic Encryption
Partially Homomorphic Encryption (PHE) allows one type of operation to be performed on ciphertext an unlimited number of times (i.e., there is no limit on usage). For example, additive homomorphism: Paillier algorithm, multiplicative homomorphism: RSA algorithm.
Somewhat Homomorphic Encryption (SWHE) allows a limited number of arbitrary operations to be performed on ciphertext (operations are unlimited, but can only be performed a limited number of times).
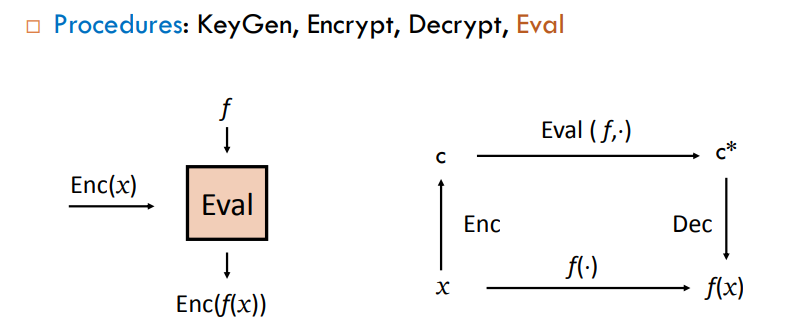
Fully Homomorphic Encryption (FHE) allows an unlimited number of arbitrary operations on ciphertext (both operations and counts are unlimited). Homomorphic encryption mainly consists of four steps: (1) KeyGen: generates a pair of secret and public keys for the asymmetric version of HE, or a single key for the symmetric version; (2) Enc: encryption; (3) Dec: decryption; KeyGen, Enc, and Dec are no different from the classic tasks in traditional encryption schemes. (4) Eval: Eval is a HE-specific operation that takes ciphertext as input and outputs ciphertext corresponding to a function’s plaintext.
3.2 Applications of Homomorphic Encryption
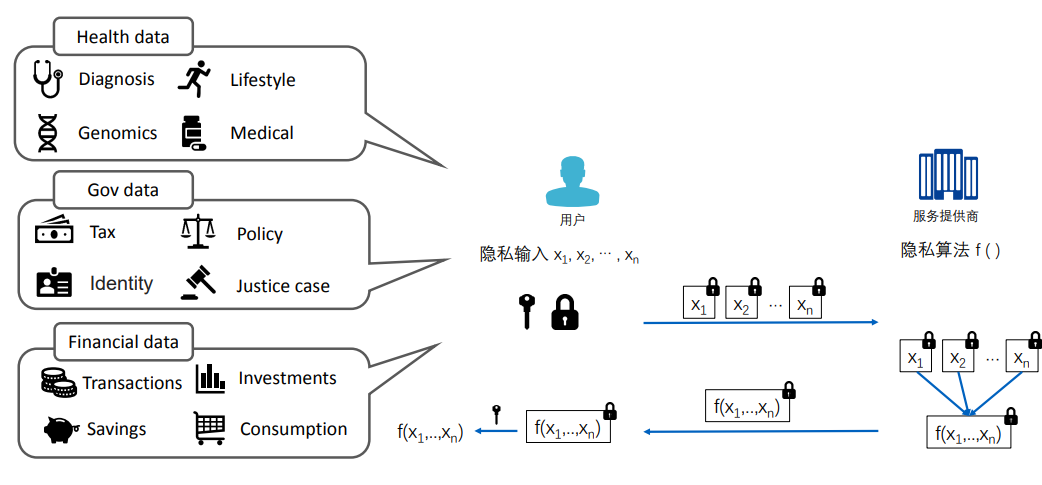
Homomorphic encryption can be applied in data protection scenarios such as health data, government data, financial data, etc. On one hand, it aims to protect data privacy and security, while on the other hand, it allows outsourcing computation tasks to computing service providers.
3.3 Symmetric and Asymmetric Homomorphic Encryption
For homomorphic encryption, symmetric encryption and public key encryption can be considered equivalent. Efficient methods already exist to convert symmetric homomorphic encryption algorithms into public key homomorphic encryption algorithms. Below is an explanation of how to convert a symmetric encryption algorithm into a public key encryption algorithm.
-
Public Key Generation
Generate l random bits, and their ciphertext (the length of l must be much greater than the length of the ciphertext).
-
To encrypt a bit value, select a random bit string r such that, output: (note: the above is calculated in modulo 2).
First Generation Homomorphic Encryption Scheme [GHDV10]
Private Key: A randomly chosen large odd integer n
Public Key: An integer, which is the noise
Encryption: Take a subset of the set and add the message
Decryption:Here the least significant bit is the message m. (The calculations here are modulo n first, then modulo 2).
Noise Issues in Homomorphic Operations
Addition: c = c1+c2, the total noise is the sum of each term’s noise.
Multiplication: c=c1*c2, the total noise is the product of each term’s noise.
From this, we can see that the noise grows exponentially, and excessive noise can affect the final decryption result.
Zhuang Zhiliang:First-year graduate student at Chongqing University, School of Big Data and Software.Main research interests include privacy-preserving machine learning and federated learning.Yuque:Achai.Zhihu:acai
Paper Notes: Release of Graph Neural Networks with Differential Privacy Guarantees
BFLC: Decentralized Federated Learning Architecture with Committee Mechanism Based on Blockchain
Differential Privacy from a Statistical Perspective
Frontiers of Federated Learning | Research on Federated Recommendation Systems Based on Graph Neural Networks
Join more discussions by adding the editor’s WeChat to join the group chat