History
Before 1976, the encryption world mainly used Symmetric-key algorithms.
Symmetric encryption has a troublesome problem: when parties A and B communicate, A must inform B of the encryption rules; otherwise, decryption is impossible.
Is it possible to ensure the security of key storage and transmission?
In 1976, two American computer scientists, Whitfield Diffie and Martin Hellman, introduced the DH key agreement algorithm.
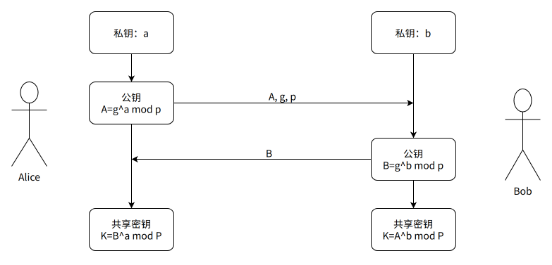
As shown above, Alice and Bob simultaneously have a shared key K, while their private keys a and b are not transmitted over the internet, and the public values A, B, g, and p cannot be used to break a, b, or K within a short time. Therefore, the DH algorithm can negotiate a key over an insecure network, establishing a secure encryption channel.
This algorithm inspired other scientists. People realized that encryption and decryption could use different rules, as long as there is some correspondence between the two rules, thus avoiding direct key transmission. This new encryption model is called Asymmetric encryption algorithm.
If the information encrypted with the public key can only be decrypted by the private key, then as long as the private key is not leaked, communication is secure.
In 1977, three mathematicians, Rivest, Shamir, and Adleman, designed an algorithm while working at the Massachusetts Institute of Technology. RSA is formed from the initials of their last names and can achieve asymmetric encryption. Since then, the RSA algorithm has been the most widely used asymmetric encryption algorithm. It is no exaggeration to say that wherever there is a computer network, there is the RSA algorithm.
In the RSA algorithm, the encryption key (i.e., the public key) PK is public information, while the decryption key (i.e., the secret key) SK must be kept confidential. The encryption algorithm E and the decryption algorithm D are also public.
PRISM
According to confidential documents provided by former NSA employee Edward Snowden, the NSA reached a $10 million contract with RSA, embedding a flawed algorithm in RSA’s encryption software to leave a “backdoor” for itself. It is reported that the software with the flawed algorithm is called Bsafe, and the flaw is named Dual Elliptic Curve, developed by the NSA.
BSafe is procured by many enterprise users for security software, allowing the NSA to easily crack various encrypted data through the backdoor program of the random number generation algorithm Bsafe.
RSA Principles
According to number theory, it is relatively simple to find two large prime numbers, but it is extremely difficult to factor their product; hence, the product can be made public as the encryption key.
Key Generation Process
| Step | Overview | Formula | Description |
|---|---|---|---|
| 1 | Random p, q | p,q | Select a pair of distinct and sufficiently large prime numbers |
| 2 | Calculate n | n = p*q | Calculate the product of prime numbers p and q |
| 3 | Calculate φ(n) | φ(n) = (p-1)(q-1) | Calculate Euler’s function for n |
| 4 | Calculate e | 1 < e < φ(n) | Select an integer e that is coprime with φ(n) |
| 5 | Calculate d | ed = 1 (mod φ(n)) | Calculate the modular inverse d of e with respect to φ(n) |
| 6 | Public Key | e,n | PK(e, n) |
| 7 | Private Key | d,n | SK(d, n) |
Step 1: Random p, q
p and q are distinct and sufficiently large primes.
Prime (Prime Number): A natural number greater than 1 that cannot be divided by any other natural number except for 1 and itself is called a prime number; otherwise, it is called a composite number (1 is neither prime nor composite).
Code Implementation:
function isPrime(num) {
for (let i = 2; i < num; i++) {
if (num % i === 0) {
return false;
}
}
return true;
}
function getPrime(min, max) {
const rst = [];
for (let i = Math.max(2, min); i <= max; i++) {
if (isPrime(i)) {
rst.push(i);
}
}
return rst;
}
// Step 1: Randomly select two distinct primes p and q
let primeList = getPrime(1, 100);
const pIndex = Math.floor(Math.random() * 1000) % primeList.length;
const p = primeList[pIndex];
primeList.splice(pIndex, 1);
const qIndex = Math.floor(Math.random() * 1000) % primeList.length;
const q = primeList[qIndex];
Step 2: Calculate n
The length of n is the key length.
n = p * q = 11 * 3 = 33;
33 in binary is 100001, which has 6 bits, so this key is 6 bits long. In practical applications, RSA keys are generally 1024 bits long, and for important scenarios, they are 2048 bits long.
Code Implementation:
// Step 2: Calculate n representing the key length
const n = p * q;
Step 3: Calculate Euler’s function φ(n)
Coprime Relationship: If two positive integers have no common factors other than 1, we say they are coprime. For instance, 15 and 32 have no common factors, so they are coprime. Common Factor is a mathematical concept referring to an integer that can divide several integers simultaneously, which can be calculated using the Euclidean algorithm.
Question: Do any two composite numbers have a coprime relationship?
For example, 15 and 44 illustrate that non-prime numbers can also form coprime relationships.
Coprime Relationship Conclusion
1. Any two prime numbers are coprime, such as 13 and 61.
2. If one number is prime and the other is not a multiple of the first, they are coprime, such as 3 and 10.
3. If the larger of the two numbers is prime, they are coprime, such as 97 and 57.
4. 1 and any natural number are coprime, such as 1 and 99.
5. If p is an integer greater than 1, then p and p-1 are coprime, such as 57 and 56.
6. If p is an odd integer greater than 1, then p and p-2 are coprime, such as 17 and 15.
Euler’s Function
For any given positive integer n, how many positive integers less than or equal to n are coprime with n? (For instance, φ(8) indicates how many numbers are coprime with 8 among the integers from 1 to 8.)
The method for calculating this value is called Euler’s function, denoted by φ(n). In the range from 1 to 8, the numbers coprime with 8 are 1, 3, 5, and 7, so φ(n) = 4.
Calculating φ(n) is not complicated, but to arrive at the final formula, we need to discuss it step by step.
| Condition | Formula | Explanation |
|---|---|---|
| If n=1 | φ(1) = 1 | Because 1 is coprime with any number (including itself). |
| If n is prime | φ(n)=n-1 | Because a prime number is coprime with every number less than it. For example, 5 is coprime with 1, 2, 3, and 4. |
|
If n is a power of a prime, n = p^k (p is prime, k is an integer greater than or equal to 1) |
φ(p^k) = p^k – p^k-1 = p^k * (1 – 1/p) |
For example, φ(8) = φ(2^3) = 2^3 – 2^2 = 8 – 4 = 4. This is because only when a number does not contain the prime p can it be coprime with n. The numbers containing the prime p total p^(k-1), which are 1×p, 2×p, 3×p, …, p^(k-1)×p. Removing these, what remains are the numbers coprime with n. When k=1, this is the second case. |
|
If n can be factored into the product of two coprime integers |
φ(n) = φ(q * p) = φ(q)φ(p) |
The Euler function of a product equals the product of the Euler functions of each factor. For example, φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24. |
| Because any integer greater than 1 can be expressed as a product of prime numbers. |
n = p1^k1 * p2^k2… φ(n) = φ(p1^k1) * φ(p2^k2)… φ(n) = p1^k1 * p2^k2 * (1 – 1/p1)(1 – 1/p2) φ(n) = n(1 – 1/p1)(1 – 1/p2)… |
φ(33) = φ(3 * 11) = 33 * (1-1/3) * (1-1/7) = 33*2/3*10/11 |
|
Based on Euler’s function, calculate φ(n) φ(n) = φ(pq) = φ(p) φ(q) = (p-1)(q-1) |
|---|
Code Implementation:
// Step 3: Calculate Euler's function φ(n)
const oN = (p - 1) * (q - 1);
Step 4: Calculate e
Randomly select an integer e such that 1< e < φ(n), and e is coprime with φ(n).
So, is it just finding a number less than φ(n) that has a greatest common divisor of 1 with φ(n)? That number is e?
Euclidean Algorithm
Finding the greatest common divisor (GCD) is called the Euclidean algorithm (also known as the method of successive divisions), represented by the formula: gcd(a,b) = gcd(b,a mod b)
The specific method is: divide the larger number by the smaller number, then use the remainder (the first remainder) to divide the divisor, and continue using the remainder (the second remainder) to divide the first remainder, and so on, until the last remainder is 0. If we are finding the GCD of two numbers, the last divisor is the GCD of those two numbers.
For example: Finding the GCD of 68 and 3
68 % 3 = 2;
3 % 2 = 1;
2 % 1 = 0;
// So the GCD of 68 and 3 is 1
// Finding the GCD of 68 and 4
68 % 4 = 0;
// So the GCD of 68 and 4 is 4
Code Implementation:
function gcd(a, b) {
// return b === 0 ? a : gcd(b, a%b)
let big = a;
let small = b;
if (a < b) {
big = b;
small = a;
}
return big % small === 0 ? small : gcd(big % small, small);
}
Now, as long as gcd(x, φ(n))===1, x is the e we are looking for, because there are multiple numbers that are coprime with φ(n) under the condition 1< e < φ(n), we can list all coprime numbers and randomly select one as e.
Code Implementation:
const primeList = [];
for (let i = 1; i < oN; i++) {
if (gcd(i, oN) === 1) {
primeList.push(i);
}
}
const index = Math.floor(Math.random() * (primeList.length - 1)) + 1;
const e = primeList[index];
Step 5: Calculate d
Calculate the modular inverse d of e with respect to φ(n), according to Euler’s theorem, we derive the following formula:ed ≡ 1 (mod φ(n))
Euler’s Theorem
The Euler function is calculated based on Euler’s theorem.
If two positive integers a and m are coprime, then the Euler function φ(m) can satisfy the following equation:
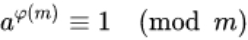
That is, the φ(m)th power of a mod m equals 1. Or, a raised to the φ(m)th power minus 1 is divisible by m.
For instance, 3 and 7 are coprime, and φ(7) equals 6, so 3 raised to the 6th power (729) minus 1 is divisible by 7 (728/7=104).
For example, to find the coprime relationship of 3 and 5, according to Euler’s theorem:
3^φ(5) = 1 (mod 5);
3^4 mod 5 = (3^4)%5 = 1;
Euler’s theorem has a special case.
Assuming that the positive integer a is coprime with the prime p, since φ(p) equals p-1, Euler’s theorem can be expressed as:
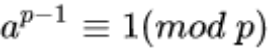
This is known as Fermat’s Little Theorem. It is a special case of Euler’s theorem.
Euler’s theorem is the core of the RSA algorithm. Understanding this theorem allows for understanding RSA.
Modular Inverse
The modular inverse is also known as the modular reciprocal or modular inverse element.
An integer a’s modular inverse with respect to a modulus n is an integer b that satisfies the following formula:
The formula is a theorem; to derive it, please refer to the derivation of the theorem.
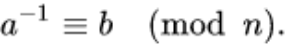
It can also be expressed in the following form (theorem):
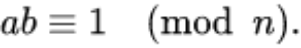
Or:
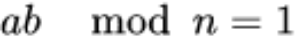
Explanation: If two positive integers a and n are coprime, then there must be an integer b such that ab-1 is divisible by n, or ab mod n equals 1.
In this case, b is called the “modular inverse” of a.
For example: 3 and 11 are coprime, so the modular inverse of 3 is 4, since (3 × 4)-1 is divisible by 11. Clearly, there are multiple modular inverses; adding or subtracting multiples of 11 from 4 yields other modular inverses of 3 {…,-18,-7,4,15,26,…}. In other words, if b is a modular inverse of a, then b + kn are also modular inverses of a.
The existence of the modular inverse can be proven using the above Euler’s theorem:
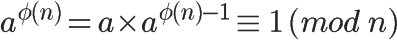
It can be seen that the φ(n)-1 power of a is the modular inverse of a.
Transform the above formula:
ed ≡ 1 (mod φ(n))
ed - 1 = k*φ(n)
**ed + φ(n)k = 1**
ax + by = 1
Since e and φ(n) are known, we are actually solving the two-variable linear equation for d and k.
Assuming e=17, φ(n)=3120, the above formula transforms to:
17x + 3120y = 1
How do we solve this two-variable linear equation?
Extended Euclidean Algorithm
Use the extended Euclidean algorithm to compute the multiplicative inverse.
The extended Euclidean algorithm can find integers x and y (one of which may be negative) while determining the GCD of integers a and b, satisfying the Bézout’s identity:
If a is negative, we can transform the problem into ∣a∣(−x)+by=gcd(∣a∣,b)
|a| is the absolute value of a, then let:
x’=(-x)
The stopping condition of the Euclidean algorithm is:
a=gcd(a,b), b=0; x=1
Since the Euclidean algorithm:
gcd(a, b) = gcd(b, amodb)
We have:
gcd(a,b) = ax+by
gcd(b, amodb) = bx1 + (amodb)y1
So:
ax+bx = bx1 + (a- ⌊a/b⌋b)y1
ax+bx = by1 + b(x1- ⌊a/b⌋y1)
Deriving we get: x = y1
y=x1−⌊a/b⌋y1
We recursively solve the first layer for x1, y1, then keep iterating to the previous layer, recursively until a set of particular solutions x=1, y=0 is reached. That is: when b = 0, ax+by = a, hence x=1, y=0.
Algorithm Implementation:
#include <bits/stdc++.h>
using namespace std;
int ext_euc(int a, int b, int &x, int &y)
{
if (b == 0)
{
x = 1, y = 0;
return a;
}
int x1, y1, d;
int d = ext_euc(b, a % b, x1, y1);
x = y1;
y = x1 - a/b * y1;
return d;
}
int main()
{
int a, b, x, y;
cin >> a >> b;
ext_euc(a, b, x, y);
cout << x << ' ' << y << endl;
return 0;
}
Simulated Execution:
Assuming p=3, q=5, e=5, φ(n)=(3-1)*(5-1)=8
ext_euc(8,5,x,y) {d = ext_euc(5,1,x,y)}
ext_euc(5,1,x,y){d = ext_euc(1,0,x,y)}
ext_euc(1,0,x,y){x=1,y=0,return 1;}
ext_euc(5,1,x,y){d=1,x=0,y=1-5/1*0=1,return 1;}
ext_euc(8,5,x,y){d=1,x=1,y=0-8/5*1=-1,return 1;}
Obtaining x = 1, y = -1;
JavaScript Code Implementation:
const xyObj = { x: null, y: null };
function exGCD(a, b, xyObj) {
// Special solution ax + 0 * y = gcd(a, b); when x=1, b=0, a = gcd(a, 0);
if (b === 0) {
xyObj.x = 1;
xyObj.y = 0;
return a;
}
const ans = exGCD(b, a % b, xyObj);
const { x, y } = xyObj;
xyObj.y = x - Math.floor(a / b) * y;
xyObj.x = y;
return ans;
}
// e*x + oN*y = 1
exGCD(e, oN, xyObj);
while (xyObj.x < 0) {
xyObj.x += oN;
}
const d = xyObj.x;
Step 6: Public and Private Keys
Public Key: PK(n, e)
Private Key: SK(n, d)
Encryption
Encryption requires the public key (n,e), and the encryption process calculates c, equivalent to the formula of m raised to the e power modulo n, where m is the object to be encrypted, and m must be an integer less than n.
Assuming A’s public key is (23, 3), and B’s m is 65, then the following equality is calculated:
The public key (n,e) can only encrypt integers less than n; what if we need to encrypt integers greater than n?
Decryption
Decryption requires the private key (n,d), and the decryption process calculates m, equivalent to c raised to the d power modulo n.
Private Key Proof
Based on the encryption formula, we need to prove the key rule:
Equivalent to proving:
Since
ed ≡ 1 (mod φ(n))
ed = hφ(n) + 1
Substituting ed yields:
-
If m is coprime with n, according to Euler’s theorem:
Obtaining:
-
If m and n are not coprime
See: RSA Encryption Algorithm【Wikipedia】
Reliability of RSA Algorithm
Is it possible to derive d when the public key PK(n, e) is known?
(1) ed≡1 (mod φ(n)). Only knowing e and φ(n) allows us to calculate d.
(2) φ(n)=(p-1)(q-1). Only knowing p and q allows us to calculate φ(n).
(3) n=pq. Only by factoring n can we find p and q.
Conclusion: If n can be factored, d can be calculated, which means the private key is compromised.
However, to this day, no one has found a polynomial-time algorithm to factor a large integer, nor has anyone proven that such an algorithm does not exist. Currently, apart from brute-force attacks, no other effective methods have been discovered.
The difficulty of factoring extremely large integers determines the reliability of the RSA algorithm. In other words, the more difficult it is to factor an extremely large integer, the more reliable the RSA algorithm.
If someone finds a fast factoring algorithm, the reliability of RSA would drop significantly. However, the likelihood of finding such an algorithm is very low. Today, only short RSA keys may be vulnerable to brute-force attacks. To date, there is no reliable method to attack the RSA algorithm.
According to disclosed literature, the longest RSA key that has been cracked is 768 bits. As long as the key length is sufficiently long, information encrypted with RSA is practically unbreakable.
It is generally believed that a 1024-bit RSA key is basically secure, while a 2048-bit key is extremely secure.
References
https://zh.wikipedia.org/zh-cn/RSA%E5%8A%A0%E5%AF%86%E6%BC%94%E7%AE%97%E6%B3%95
https://zh.wikipedia.org/wiki/%E6%A8%A1%E5%8F%8D%E5%85%83%E7%B4%A0
https://zh.wikipedia.org/wiki/扩展欧几里得算法
https://zh.wikipedia.org/wiki/%E8%BC%82%E8%BD%89%E7%9B%B8%E9%99%A4%E6%B3%95
https://www.bilibili.com/video/BV1rD4y1C7qg/?zw
https://juejin.cn/post/7044863141062115341
https://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html
https://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html
https://www.aqniu.com/news-views/942.html
– END –
About Qiwutuan
Qiwutuan is the largest front-end team of 360 Group, representing the group to participate in W3C and ECMA member (TC39) work.Qiwutuan values talent cultivation and offers various development directions for its employees, including engineers, lecturers, translators, business liaisons, team leaders, and more, along with corresponding technical, professional, general, and leadership training courses.Qiwutuan welcomes all kinds of outstanding talents to pay attention to and join the team with an open and talent-seeking attitude.
