Last time, the author introduced some number theory knowledge.
With this knowledge, we can understand the RSA algorithm. This is currently the most important encryption algorithm on Earth.


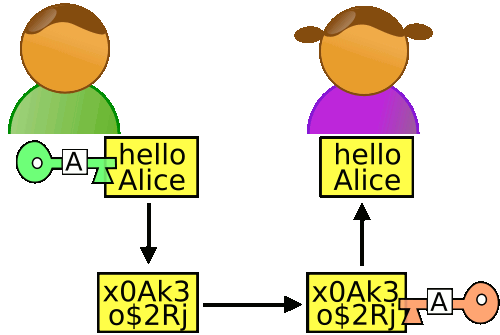
We will understand the RSA algorithm through an example. Suppose Alice wants to communicate securely with Bob, how should she generate her public and private keys?
Alice chooses 61 and 53. (In practical applications, the larger these prime numbers are, the harder they are to crack.)
Alice multiplies 61 and 53.
n = 61 × 53 = 3233
The length of n is the key length. 3233 in binary is 110010100001, which has 12 bits, so this key is 12 bits long. In practical applications, RSA keys are generally 1024 bits, and in important scenarios, they can be 2048 bits long.
According to the formula:
φ(n) = (p-1)(q-1)
Alice calculates φ(3233) as 60 × 52, which equals 3120.
Alice randomly selects 17 between 1 and 3120. (In practical applications, 65537 is often chosen.)
The so-called “modular inverse” means there exists an integer d such that ed leaves a remainder of 1 when divided by φ(n).
ed ≡ 1 (mod φ(n))
This equation is equivalent to
ed – 1 = kφ(n)
Thus, finding the modular inverse d essentially involves solving the following linear Diophantine equation.
ex + φ(n)y = 1
Given e = 17, φ(n) = 3120,
17x + 3120y = 1
This equation can be solved using the “Extended Euclidean Algorithm”; the specific process is omitted here. In summary, Alice finds a set of integer solutions (x,y) = (2753,-15), thus d = 2753.
All calculations are now complete.
In Alice’s case, n = 3233, e = 17, and d = 2753, so the public key is (3233, 17), and the private key is (3233, 2753).
In practical applications, both public and private key data are expressed in ASN.1 format (example).

Reviewing the key generation steps, a total of six numbers appear:
p, q, n, φ(n), e, d
Among these six numbers, the public key uses two (n and e), while the other four numbers are not public. The most critical is d, as n and d form the private key; once d is leaked, it is equivalent to leaking the private key.
So, is it possible to derive d knowing n and e?
(1) ed ≡ 1 (mod φ(n)). Only knowing e and φ(n) allows us to calculate d.
(2) φ(n) = (p-1)(q-1). Only knowing p and q allows us to calculate φ(n).
(3) n = pq. Only by factoring n can we find p and q.
Conclusion: If n can be factored, d can be calculated, which means the private key is compromised.
However, factoring large integers is a very difficult task. Currently, apart from brute force attacks, no other effective methods have been discovered. Wikipedia states:
” The difficulty of factoring extremely large integers determines the reliability of the RSA algorithm. In other words, the harder it is to factor an extremely large integer, the more reliable the RSA algorithm.
If someone finds a fast factoring algorithm, the reliability of RSA will drastically decline. However, the likelihood of finding such an algorithm is very low. Today, only short RSA keys can be brute-forced. As of 2008, there has been no reliable method to attack the RSA algorithm.
As long as the key length is sufficiently long, information encrypted with RSA is practically unbreakable.“
For example, you can factor 3233 (61 × 53), but you cannot factor the following integer.
1230186684530117755130494958384962720772853569595334792197322452151726400507263657518745202199786469389956474942774063845925192557326303453731548268507917026122142913461670429214311602221240479274737794080665351419597459856902143413
It is the product of these two prime numbers:
33478071698956898786044169848212690817704794983713768568912431388982883793878002287614711652531743087737814467999489 × 36746043666799590428244633799627952632279158164343087642676032283815739666511279233373417143396810270092798736308917
In fact, this is probably the largest integer that has been factored by humans (232 decimal digits, 768 binary digits). No larger factors have been reported, so the longest RSA key that has been cracked so far is 768 bits.

With the public and private keys, encryption and decryption can be performed.
(1) Encryption uses the public key (n,e)
Suppose Bob wants to send encrypted information m to Alice, he needs to encrypt m using Alice’s public key (n,e). It is important to note that m must be an integer (strings can be converted to ASCII or Unicode values), and m must be less than n.
Encryption means calculating c as follows:
me ≡ c (mod n)
Alice’s public key is (3233, 17), and let’s assume Bob’s m is 65, then the following equation can be calculated:
6517 ≡ 2790 (mod 3233)
Thus, c equals 2790, and Bob sends 2790 to Alice.
(2) Decryption uses the private key (n,d)
After Alice receives 2790 from Bob, she uses her private key (3233, 2753) to decrypt it. It can be proven that the following equation will always hold:
cd ≡ m (mod n)
In other words, c raised to the power of d modulo n equals m. Now, c equals 2790, and the private key is (3233, 2753), so Alice calculates
27902753 ≡ 65 (mod 3233)
Therefore, Alice knows that the original message before Bob’s encryption was 65.
Thus, the entire process of “encryption–decryption” is completed.
We can see that without knowing d, it is impossible to derive m from c. And as mentioned earlier, to know d, one must factor n, which is extremely difficult to do, thus ensuring the security of RSA communication.
You may ask, if the public key (n,e) can only encrypt integers m less than n, what should be done if we want to encrypt integers greater than n? There are two solutions: one is to split long messages into several shorter segments, each of which is encrypted separately; the other is to first select a symmetric encryption algorithm (such as DES), use this algorithm’s key to encrypt the information, and then encrypt the DES key with the RSA public key.
Finally, let’s prove why decrypting with the private key can correctly obtain m. That is, to prove the following equation:
cd ≡ m (mod n)
Because, according to the encryption rule
m^e ≡ c (mod n)
Thus, c can be expressed as:
c = m^e – kn
Substituting c into the decryption rule we want to prove:
(m^e – kn)d ≡ m (mod n)
This is equivalent to proving
m^{ed} ≡ m (mod n)
Since
ed ≡ 1 (mod φ(n))
So
ed = hφ(n)+1
Substituting ed gives:
m^{hφ(n)+1} ≡ m (mod n)
Next, we will prove this equation in two cases.
(1) m is coprime to n.
According to Euler’s theorem, in this case
m^{φ(n)} ≡ 1 (mod n)
Thus we obtain
(m^{φ(n)})^h × m ≡ m (mod n)
The original equation is proven.
(2) m is not coprime to n..
In this case, since n is the product of the primes p and q, m must equal kp or kq.
Taking m = kp as an example, considering that k must be coprime to q, we have according to Euler’s theorem:
(kp)^{q-1} ≡ 1 (mod q)
Further leading to
[(kp)^{q-1}]^h(p-1) × kp ≡ kp (mod q)
That is
(kp)^{ed} ≡ kp (mod q)
Rewriting gives the following equation
(kp)^{ed} = tq + kp
Here t must be divisible by p, thus t = t’p
(kp)^{ed} = t’pq + kp
Since m = kp and n = pq, we have
m^{ed} ≡ m (mod n)
The original equation is proven.
RSA Algorithm Principles (Part 1)
Source: Scientific Squirrel Society
∑ Edited by / Douzhi