In recent years, security incidents involving industrial control systems have been frequent, and there is a lack of effective quantitative risk assessment methods domestically. To address this issue, a quantitative assessment method for industrial control system security based on the combination of fuzzy analytic hierarchy process and attack tree models is proposed. This method establishes a hierarchical analysis model for typical industrial control systems, combines group decision-making by inviting multiple experts to assign relative importance to the elements at each level to obtain a judgment matrix, and performs fuzzification on the judgments. Finally, an attack tree model is established for each type of attack on the industrial control system to quantitatively analyze the probability of each attack occurring, and targeted protective measures are taken based on the aforementioned system vulnerabilities. Experimental results show that this method is effective.
With the continuous popularization and development of information technology, in recent years, network attacks have not only been limited to information systems but have gradually appeared in industrial control systems (Industrial Control System, ICS), severely affecting the national economy and people’s livelihood, causing huge economic losses and social harm. From the investigation report of the Industrial Control System Investigation Team (ICS-IT), it can be seen that approximately 865 security incidents occurred from 2015 to 2019. Faced with numerous security incidents, how to establish effective industrial safety protection technologies has become particularly urgent.
In recent years, many scholars have been continuously exploring this field from theory to practice and have achieved some results. A typical example is the quantitative assessment of security risk factors adopted by Yang Xiangdong and others, which involve assets, threats, vulnerabilities, and security measures. Yang Xiangdong quantified these four factors in conjunction with corresponding standards to obtain the system’s risk value. This method clearly obtains the overall security attributes of the system, but it does not consider the impact of each specific attack method, nor does it take into account the interactions between various attack methods. PENG Y J and others applied Bayesian networks to industrial control security assessment, establishing probabilistic models to describe various factors affecting security, which can analyze not only the overall risk of the system but also the risks caused by each factor in the system. However, determining the conditional probabilities of the network model is extremely complex and is not suitable for application in specific security scenarios. In recent years, people have begun to focus on the Analytic Hierarchy Process (AHP), which can establish a hierarchical analysis model based on specific industrial systems, treating various attack factors as evaluation layers, and using the final risk evaluation results as target layers. However, this method is highly subjective in determining the judgment matrix and cannot effectively achieve quantification.
This article proposes a method combining fuzzy analytic hierarchy (Fuzzy Analytic Hierarchy Process, FAPH) and attack trees, establishing a hierarchical analysis model for the system, allowing multiple experts to score the importance of each factor to establish a judgment matrix. To address the issue that the fuzzy analytic hierarchy method cannot accurately analyze the occurrence probability of each attack factor and its impact on the factor layer, this article integrates the attack tree model into the fuzzy analytic hierarchy method to quantitatively calculate the occurrence probability of each attack method.
1 Necessity of Integrating Functional Safety and Information Security in Industrial Control Systems
The failure of safety functions in industrial control systems can be caused not only by threat entities through network attacks but also by internal system issues. Therefore, the functional safety and information security of industrial control systems are not entirely independent. Establishing an effective comprehensive safety quantitative assessment system helps to timely understand the safety indicators of industrial control systems and prevent safety accidents from occurring.
To establish a comprehensive safety quantitative assessment system, it is necessary first to clarify the differences between functional safety and information security. Researchers in various fields have discrepancies in their understanding of functional safety and information security. According to the National Institute of Standards and Technology (NIST) in the United States, which released NIST SP-80053 (security controls for federal information and information systems), the differences between ICS information security and functional safety are briefly outlined in Table 1. It can be seen that the main difference between functional safety and information security is that threats to functional safety come from internal sources, caused by hardware failures or human errors, while threats to information security come from external sources such as hacker attacks.
Table 1Comparison of Functional Safety and Information Security Attributes
Understanding the differences between functional safety and information security helps to comprehensively consider the impacts of both when establishing industrial control system models, thereby providing the most comprehensive safety quantification for industrial control systems.
2 Basic Concepts of Hierarchical Model and Attack Tree Model
In the quantitative assessment of industrial control system security based on fuzzy analytic hierarchy process, the most important task is to establish a hierarchical model. The national standard GB/T20984-2007 clearly states that information security risk analysis is divided into three aspects: assets, vulnerabilities, and threats. Attackers utilize the vulnerabilities of information systems to pose security threats to the system, resulting in losses to the system’s assets.
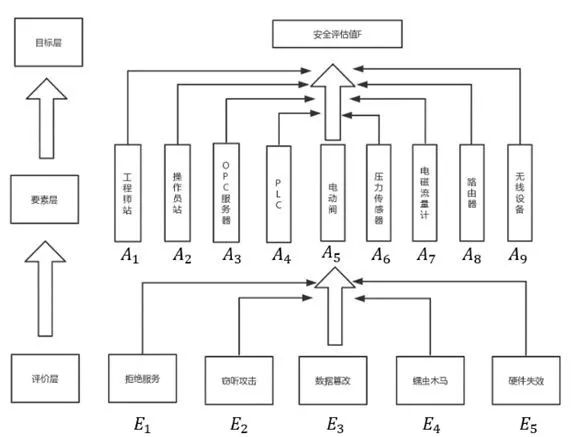
The Analytic Hierarchy Process (AHP) was first proposed by American operations research expert Satty TL and is a multi-criteria decision-making method for handling complex systems. In a typical hierarchical analysis method, the entire system is divided into a target layer, an element layer, and an evaluation layer. Analogous to the three elements of asset, threat, and vulnerability in information security analysis, the evaluation layer in the hierarchical analysis method is represented as various security attacks on the system, the element layer represents the various devices of the system, and the target layer represents the final security evaluation value of the system.
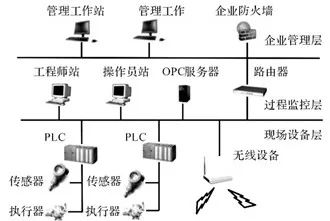
When applied to actual industrial control systems, due to the complexity of the system, it is necessary to first determine the network structure of the system to gain a deeper understanding of the elements to be analyzed and the evaluation objects. According to the hierarchical structure proposed in the national standard GB/T26333-201, the system is divided into three layers: enterprise management layer, process monitoring layer, and field device layer, as shown in Figure 1. Since the process monitoring layer and field device layer are closely related to the industrial control field, they will be the focus of analysis in practical analysis.
Figure 1 Typical Hierarchical Structure of Industrial Control Systems
2.2.1 Basic Concept of Attack Tree Model
The attack tree model is a visualization method proposed by Schneider in the late 20th century to describe the attacks on a system, using a tree structure to represent the entire system, with leaf nodes representing specific attack events and the root node representing the final target being attacked. Except for the lowest leaf nodes, the other nodes are divided into AND and OR types. In the AND type, all the leaves in the next layer of the root node must be completed to reach the root node. In contrast, in the OR type, completing any one leaf node can complete the attack on the root node. The graphical representation of the AND and OR of the attack tree model is shown in Figure 2.
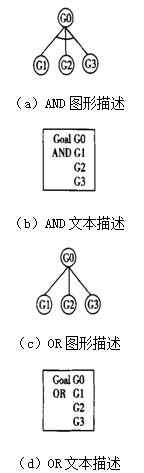
Figure 2 Graphical Representation of AND and OR in Attack Tree Model
2.2.2 Calculation of Leaf Node Probability Values in Attack Tree Model
In risk assessment, the loss caused by attack events is often used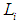 multiplied by the probability value of the attack event occurring
multiplied by the probability value of the attack event occurring as the risk assessment value
as the risk assessment value , that is:
When calculating the probability value of the root node, the leaf nodes must be quantified. According to the guidelines for industrial control system security defined by the United States, the probability of an attack event occurring is affected by three factors: attack cost, attack difficulty, and the possibility of being discovered. When calculating the probability value of each leaf node, these three attributes must be considered. Based on multi-attribute utility theory, these three attributes can be converted into utility values, leading to the probability value calculation formula for each leaf node:
, that is:
When calculating the probability value of the root node, the leaf nodes must be quantified. According to the guidelines for industrial control system security defined by the United States, the probability of an attack event occurring is affected by three factors: attack cost, attack difficulty, and the possibility of being discovered. When calculating the probability value of each leaf node, these three attributes must be considered. Based on multi-attribute utility theory, these three attributes can be converted into utility values, leading to the probability value calculation formula for each leaf node:
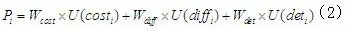 In formula (2),
In formula (2), 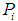 represents the occurrence probability,
represents the occurrence probability,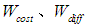 and
and 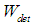 represent the weights of attack cost, attack difficulty, and the possibility of being discovered, respectively, with the sum of the three weights equal to 1. In the case analysis, the fuzzy analytic hierarchy method will be used to determine the specific values of these three weights.
represent the weights of attack cost, attack difficulty, and the possibility of being discovered, respectively, with the sum of the three weights equal to 1. In the case analysis, the fuzzy analytic hierarchy method will be used to determine the specific values of these three weights.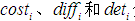 represent the levels of attack cost, difficulty, and the possibility of being discovered.
represent the levels of attack cost, difficulty, and the possibility of being discovered.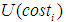 , and
, and 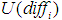 and
and 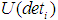 represent the utility values of attack cost
represent the utility values of attack cost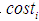 , attack difficulty
, attack difficulty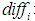 , and the possibility of being discovered
, and the possibility of being discovered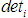 utility values. Further analysis can lead to
utility values. Further analysis can lead to 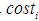 ,
, 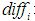 ,
, 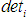 and the utility values are inversely proportional. To simplify the analysis, let’s take
and the utility values are inversely proportional. To simplify the analysis, let’s take 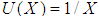 .
2.2.3 Calculation of Node Probability Values
After obtaining the probability values of each leaf node, the probability value of the root node can be calculated. The discussion is divided into two cases: AND and OR:
(1) The probability value of the AND node is the product of the probability values of all leaf nodes, namely:
(2) The OR node is the maximum value of the occurrence probabilities of all leaf nodes, that is:
.
2.2.3 Calculation of Node Probability Values
After obtaining the probability values of each leaf node, the probability value of the root node can be calculated. The discussion is divided into two cases: AND and OR:
(1) The probability value of the AND node is the product of the probability values of all leaf nodes, namely:
(2) The OR node is the maximum value of the occurrence probabilities of all leaf nodes, that is:
3 Case Study Analysis of Typical Scenarios
Applying Fuzzy Analytic Hierarchy Process (FAHP) to industrial control systems to solve actual safety quantification issues generally involves four steps: (1) establish a hierarchical analysis model based on the specific problem; (2) construct pairwise judgment matrices for the evaluation layer elements against the element layer and the element layer against the target layer; (3) calculate the relative weights of the compared elements from the judgment matrices; (4) calculate the combined weights of each element in the evaluation layer and element layer.
3.1 Establishing a Hierarchical Model for a Typical Industrial Control Site
Taking a certain power equipment system as a research object, a hierarchical analysis model based on FAPH is established for the process monitoring layer and field device layer, as shown in Figure 3. The target layer is the security evaluation value of the industrial control system, and the element layer includes various system devices such as engineer stations, operator stations, PLCs, various sensors, flow meters, and wireless devices.
Figure 3 Hierarchical Analysis Model of Industrial Control System Based on FAHP
3.2 Constructing Pairwise Judgment Matrices
After completing the hierarchical modeling of the system, it is necessary to quantitatively analyze the impact of each layer’s elements on the previous layer’s elements when damaged, and then establish the relative importance judgment matrix for the elements. To do this, a scale of 0.1 to 0.9 is used to assign values to the relative importance of two elements, as shown in Table 2.
Table 2 Scale of Priority Relationship Values for Elements
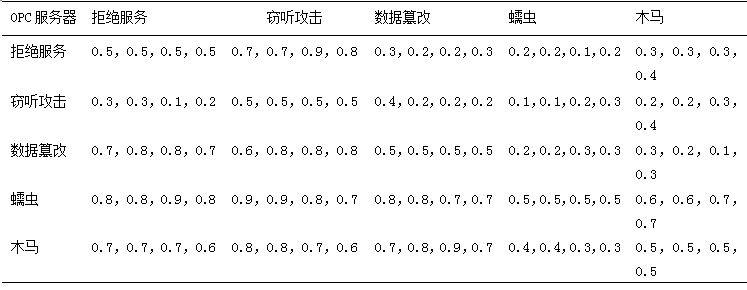
 The specificity of the five security threats in the evaluation layer leads to significant differences in their impact on a certain device in the element layer. Based on Table 2, a judgment matrix can be established for the impact of the five attack methods on the device layer. Taking the OPC server as an example, the impact of the five attack methods from the evaluation layer is assessed based on the effects caused after being attacked, leading to the assignment of judgment values. Data tampering can allow attackers to obtain core data from the OPC server, and the entire attack process is difficult to detect, causing serious harm. Denial of service causes the OPC server to lose control over the lower-level systems, leading to information chaos, but this type of attack that causes the system to lose control is easier to detect, and corresponding remedial measures can be taken, resulting in relatively minor impacts. Eavesdropping attacks will result in the theft of data from the OPC system, which is less impactful compared to data tampering that directly paralyzes the system. Worms and Trojans can modify the service programs of the OPC, diminishing some of its capabilities.
Based on the above analysis, four experts are invited to assign values to the impact of these five attacks on the OPC server according to Table 2, resulting in the judgment assignment table as shown in Table 3. Each cell in Table 3 contains four elements, which are the judgment assignments of importance from the four experts, and the elements in the same position of the cells form the judgment matrix. Inviting multiple experts aims to avoid the subjectivity and arbitrariness of experts during the judgment process, making the evaluation results more persuasive.
Table 3 Importance Assignment of Evaluation Indicators for OPC Server
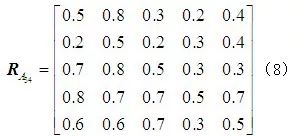
From Table 3, the four judgment matrices for the OPC server can be obtained
The specificity of the five security threats in the evaluation layer leads to significant differences in their impact on a certain device in the element layer. Based on Table 2, a judgment matrix can be established for the impact of the five attack methods on the device layer. Taking the OPC server as an example, the impact of the five attack methods from the evaluation layer is assessed based on the effects caused after being attacked, leading to the assignment of judgment values. Data tampering can allow attackers to obtain core data from the OPC server, and the entire attack process is difficult to detect, causing serious harm. Denial of service causes the OPC server to lose control over the lower-level systems, leading to information chaos, but this type of attack that causes the system to lose control is easier to detect, and corresponding remedial measures can be taken, resulting in relatively minor impacts. Eavesdropping attacks will result in the theft of data from the OPC system, which is less impactful compared to data tampering that directly paralyzes the system. Worms and Trojans can modify the service programs of the OPC, diminishing some of its capabilities.
Based on the above analysis, four experts are invited to assign values to the impact of these five attacks on the OPC server according to Table 2, resulting in the judgment assignment table as shown in Table 3. Each cell in Table 3 contains four elements, which are the judgment assignments of importance from the four experts, and the elements in the same position of the cells form the judgment matrix. Inviting multiple experts aims to avoid the subjectivity and arbitrariness of experts during the judgment process, making the evaluation results more persuasive.
Table 3 Importance Assignment of Evaluation Indicators for OPC Server
From Table 3, the four judgment matrices for the OPC server can be obtained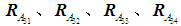 :
Similarly, the four judgment matrices for each system device in the other element layers can be obtained. Based on the impact of the element layer devices under attack on the target layer, the judgment matrix for the element layer against the target layer can also be established. The impact of attacks on the engineer station on the target layer is significantly greater than that on the operator station; the PLC’s losses to the system are difficult to detect, and since the PLC is the controllable unit downstream of the system, it is more important than the engineer station. Following the same reasoning, the importance assignment table for each device in the element layer is established, resulting in a judgment matrix
:
Similarly, the four judgment matrices for each system device in the other element layers can be obtained. Based on the impact of the element layer devices under attack on the target layer, the judgment matrix for the element layer against the target layer can also be established. The impact of attacks on the engineer station on the target layer is significantly greater than that on the operator station; the PLC’s losses to the system are difficult to detect, and since the PLC is the controllable unit downstream of the system, it is more important than the engineer station. Following the same reasoning, the importance assignment table for each device in the element layer is established, resulting in a judgment matrix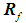 , and four experts are invited to score, with only one expert’s judgment matrix shown here:
, and four experts are invited to score, with only one expert’s judgment matrix shown here:
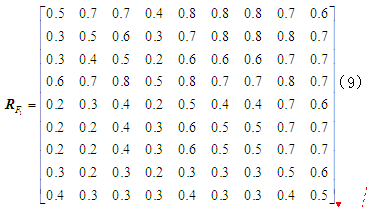 Before proceeding to the next step, the obtained judgment matrices must undergo consistency testing to determine whether they meet consistency requirements. If not, adjustments must be made, following these steps.
(1) Calculate the consistency index of the matrix
Before proceeding to the next step, the obtained judgment matrices must undergo consistency testing to determine whether they meet consistency requirements. If not, adjustments must be made, following these steps.
(1) Calculate the consistency index of the matrix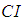 :
:
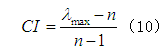
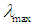 is the maximum eigenvalue of the matrix, and
is the maximum eigenvalue of the matrix, and 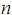 is the order of the matrix.
(2) Look up the random consistency index
is the order of the matrix.
(2) Look up the random consistency index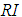 ,
, 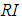 values are shown in Table 4.
Table 4 Random Consistency Index for Orders 1 to 10
values are shown in Table 4.
Table 4 Random Consistency Index for Orders 1 to 10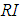 (3) Calculate the consistency ratio
(3) Calculate the consistency ratio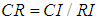 , when satisfying
, when satisfying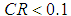 , it is considered that the judgment matrix meets the requirements; otherwise, adjustments are needed.
The judgment matrices in this example
, it is considered that the judgment matrix meets the requirements; otherwise, adjustments are needed.
The judgment matrices in this example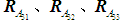 and
and 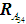 have maximum eigenvalues of 5.112, 5.024, 5.403, and 5.276, with the matrix order
have maximum eigenvalues of 5.112, 5.024, 5.403, and 5.276, with the matrix order 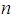 being 5, and
being 5, and 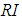 according to Table 4 is 1.12. The consistency ratios calculated are
according to Table 4 is 1.12. The consistency ratios calculated are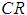 of 0.025, 0.005, 0.089, and 0.061, satisfying the consistency testing requirements. The same method is used to test the remaining matrices; if they do not meet the requirements, adjustments are made, ultimately obtaining all judgment matrices.
3.3 Calculating the Weights of Elements in This Layer Against the Upper Layer Elements
To further reduce the subjectivity of expert evaluations, the judgment matrices are fuzzified to obtain fuzzy consistent judgment matrices
of 0.025, 0.005, 0.089, and 0.061, satisfying the consistency testing requirements. The same method is used to test the remaining matrices; if they do not meet the requirements, adjustments are made, ultimately obtaining all judgment matrices.
3.3 Calculating the Weights of Elements in This Layer Against the Upper Layer Elements
To further reduce the subjectivity of expert evaluations, the judgment matrices are fuzzified to obtain fuzzy consistent judgment matrices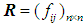 , using formulas (11) and (12) to complete the fuzzification process. After obtaining the fuzzy consistent matrix, the weights of the indicators in the evaluation layer (such as the denial of service indicator
, using formulas (11) and (12) to complete the fuzzification process. After obtaining the fuzzy consistent matrix, the weights of the indicators in the evaluation layer (such as the denial of service indicator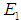 ) against the element layer system devices (such as the OPC server
) against the element layer system devices (such as the OPC server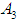 ) can be calculated.
In formula (13), the parameters
) can be calculated.
In formula (13), the parameters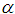 satisfy
satisfy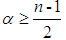 , and are inversely proportional to the differences in weights, meaning that when
, and are inversely proportional to the differences in weights, meaning that when 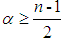 reaches its maximum, the differences in relative weights of each risk factor are maximized. In this example, n=5, leading to
reaches its maximum, the differences in relative weights of each risk factor are maximized. In this example, n=5, leading to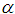 =2. The obtained judgment matrices, and their fuzzification, will lead to fuzzy consistent matrices
=2. The obtained judgment matrices, and their fuzzification, will lead to fuzzy consistent matrices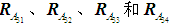 . Taking the fuzzy judgment matrix from the first expert
. Taking the fuzzy judgment matrix from the first expert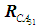 , the relative weight of the OPC server can be calculated.
, the relative weight of the OPC server can be calculated.
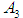 Similarly, the relative weights of the other four attack methods on the OPC server can be obtained, leading to the weight vector of the five attack indicators on the OPC server
Similarly, the relative weights of the other four attack methods on the OPC server can be obtained, leading to the weight vector of the five attack indicators on the OPC server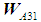 =[0.162,0.145,0.234,0.191,0.268]. Following the same approach, the weight vectors for the other three experts’ fuzzy judgment matrices
=[0.162,0.145,0.234,0.191,0.268]. Following the same approach, the weight vectors for the other three experts’ fuzzy judgment matrices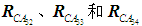 lead to the weight vectors of the five attack indicators on the OPC server as follows:
For the four obtained weight vectors, the final denial of service attack weight vector on the OPC server is obtained by taking the average of the corresponding positions:
Following the same steps, the weight vectors of the five attack methods on the other facilities in the element layer, as well as the weight vectors of the element layer against the target layer
lead to the weight vectors of the five attack indicators on the OPC server as follows:
For the four obtained weight vectors, the final denial of service attack weight vector on the OPC server is obtained by taking the average of the corresponding positions:
Following the same steps, the weight vectors of the five attack methods on the other facilities in the element layer, as well as the weight vectors of the element layer against the target layer can be calculated:
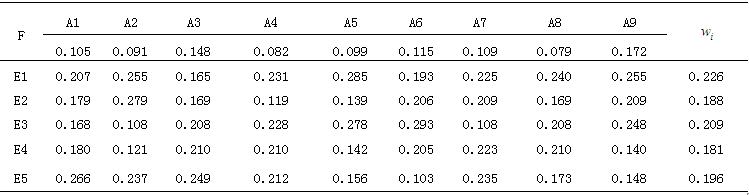
After analyzing the weights of each element against the upper layer, the comprehensive weights of each risk element in the evaluation layer against the target layer F can be obtained according to formula (28)
can be calculated:
After analyzing the weights of each element against the upper layer, the comprehensive weights of each risk element in the evaluation layer against the target layer F can be obtained according to formula (28)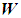 , with the entire calculation process shown in Table 5.
, with the entire calculation process shown in Table 5.
Table 5 Comprehensive Weights of Each Risk Element in the Evaluation Layer Against the Target Layer
The comprehensive weight obtained is:
The risks with the highest weight are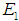 denial of service and
denial of service and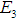 data tampering. An attack tree model is established for the five attack methods to quantitatively analyze the probability of each attack method occurring.
data tampering. An attack tree model is established for the five attack methods to quantitatively analyze the probability of each attack method occurring.
4 Establishment and Result Analysis of Attack Tree Models
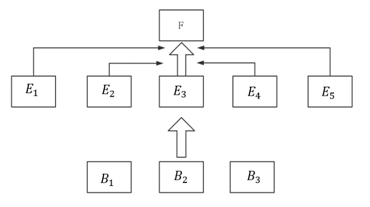
According to the analysis in section 2.2, the probability of risks occurring in the system is influenced by attack costs, attack difficulty, and the possibility of being discovered. In the above analysis, the comprehensive weights of various attack methods against the target layer have been obtained, and when establishing the attack tree model, the target layer is directly set as the attack node. The attack tree model is established as shown in Figure 4. Since all five attack methods can directly affect the system, an OR node is used in Figure 2 to establish the entire system attack tree model, and the fuzzy analytic hierarchy method is used to determine the relative weights of attack cost, attack difficulty, and the possibility of being discovered.
Figure 4 Attack Tree Model
In Figure 4, 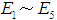 represents the five attack methods,
represents the five attack methods,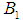 represents the attack cost, attack difficulty, and the possibility of being discovered. Taking data tampering
represents the attack cost, attack difficulty, and the possibility of being discovered. Taking data tampering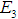 as an example, from the attacker’s perspective, they would prefer that this data tampering attack is not easily detected, giving it a greater weight than attack cost and difficulty. Increasing the attack difficulty will reduce the probability of the entire attack event, and its weight is slightly lower compared to attack cost.
Using the fuzzy analytic hierarchy method’s approach, a fuzzy judgment matrix is established, and consistency testing is performed to obtain the relative weights of the three influencing factors; here, only the final analysis results are provided.
For attack difficulty
as an example, from the attacker’s perspective, they would prefer that this data tampering attack is not easily detected, giving it a greater weight than attack cost and difficulty. Increasing the attack difficulty will reduce the probability of the entire attack event, and its weight is slightly lower compared to attack cost.
Using the fuzzy analytic hierarchy method’s approach, a fuzzy judgment matrix is established, and consistency testing is performed to obtain the relative weights of the three influencing factors; here, only the final analysis results are provided.
For attack difficulty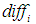 , attack cost
, attack cost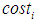 , and the possibility of being discovered
, and the possibility of being discovered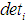 scoring standards, as shown in Table 6.
Table 6 Level Scoring Standards
scoring standards, as shown in Table 6.
Table 6 Level Scoring Standards
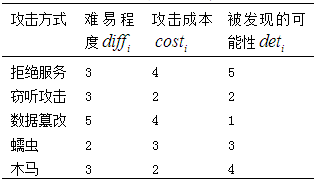
In practical applications, evaluators give level scores based on specific situations. In this industrial control system, multiple experts were invited to provide level scores, and the average value was taken to give specific scoring situations. Among the five attack methods, data tampering was rated as the most difficult, with high costs and being difficult to detect, with the corresponding three levels being 5, 4, and 1; the level scores of the other four attacks are shown in Table 7.
Table 7 Level Scores of Attack Methods
Based on formula (2), the attack probabilities of various attack methods are 0.2690, 0.4393, 0.3968, 0.3940, and 0.3843 respectively. Since these attack probabilities do not have a definite independent relationship, their sum is not 1. The weights of each attack factor obtained from the analytic hierarchy method are:
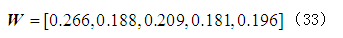
This article takes the product of the weights and probabilities as the final risk values of the five attack methods in the evaluation layer, resulting in 0.0607, 0.0825, 0.0829, 0.0713, and 0.0753, indicating that the most likely threat attacks are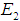 eavesdropping attacks and
eavesdropping attacks and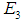 data tampering, thus emphasizing the need to strengthen prevention against eavesdropping attacks and data tampering.
This article addresses the issue of quantitative assessment of industrial control system security by proposing a method that combines fuzzy analytic hierarchy process and attack trees. The fuzzy analytic hierarchy process reduces the subjective factors of experts by establishing a fuzzy judgment matrix and further reduces the subjectivity of expert evaluations through a group decision-making approach that averages the weight vectors obtained from multiple experts. In addressing the integration of industrial control information security and functional safety, this article treats denial of service, eavesdropping attacks, data tampering, worms, Trojans, and system hardware failures as threat factors to the entire system and establishes a hierarchical analysis model. An attack tree is established to quantitatively analyze the probabilities of security threat events occurring, ultimately considering both the probabilities of security events and their weights to quantitatively analyze the system’s risk.
Future research can continue in the following areas: (1) In quantitative analysis, expert judgment results can be influenced by subjective factors. This article only determines the final weights of threat factors by averaging expert judgment results; establishing a more effective quantification method will be a focus of future research; (2) Given the complexity of industrial control systems, further consideration is needed on how to establish a more comprehensive hierarchical analysis model; (3) This article focuses on the individual impacts of the five threat factors on the system and does not address the overall safety quantification value of the system under the influence of these five threats, which will be a key focus of future research.
Source: Journal of Information Security and Communication Confidentiality
data tampering, thus emphasizing the need to strengthen prevention against eavesdropping attacks and data tampering.
This article addresses the issue of quantitative assessment of industrial control system security by proposing a method that combines fuzzy analytic hierarchy process and attack trees. The fuzzy analytic hierarchy process reduces the subjective factors of experts by establishing a fuzzy judgment matrix and further reduces the subjectivity of expert evaluations through a group decision-making approach that averages the weight vectors obtained from multiple experts. In addressing the integration of industrial control information security and functional safety, this article treats denial of service, eavesdropping attacks, data tampering, worms, Trojans, and system hardware failures as threat factors to the entire system and establishes a hierarchical analysis model. An attack tree is established to quantitatively analyze the probabilities of security threat events occurring, ultimately considering both the probabilities of security events and their weights to quantitatively analyze the system’s risk.
Future research can continue in the following areas: (1) In quantitative analysis, expert judgment results can be influenced by subjective factors. This article only determines the final weights of threat factors by averaging expert judgment results; establishing a more effective quantification method will be a focus of future research; (2) Given the complexity of industrial control systems, further consideration is needed on how to establish a more comprehensive hierarchical analysis model; (3) This article focuses on the individual impacts of the five threat factors on the system and does not address the overall safety quantification value of the system under the influence of these five threats, which will be a key focus of future research.
Source: Journal of Information Security and Communication Confidentiality





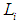 multiplied by the probability value of the attack event occurring
multiplied by the probability value of the attack event occurring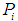 as the risk assessment value
as the risk assessment value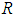 , that is:
, that is: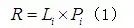
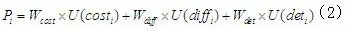
 represents the occurrence probability,
represents the occurrence probability, and
and 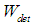 represent the weights of attack cost, attack difficulty, and the possibility of being discovered, respectively, with the sum of the three weights equal to 1. In the case analysis, the fuzzy analytic hierarchy method will be used to determine the specific values of these three weights.
represent the weights of attack cost, attack difficulty, and the possibility of being discovered, respectively, with the sum of the three weights equal to 1. In the case analysis, the fuzzy analytic hierarchy method will be used to determine the specific values of these three weights.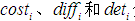 represent the levels of attack cost, difficulty, and the possibility of being discovered.
represent the levels of attack cost, difficulty, and the possibility of being discovered.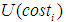 , and
, and 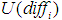 and
and 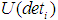 represent the utility values of attack cost
represent the utility values of attack cost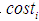 , attack difficulty
, attack difficulty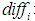 , and the possibility of being discovered
, and the possibility of being discovered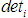 utility values. Further analysis can lead to
utility values. Further analysis can lead to 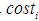 ,
, 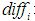 ,
, 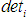 and the utility values are inversely proportional. To simplify the analysis, let’s take
and the utility values are inversely proportional. To simplify the analysis, let’s take 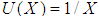 .
.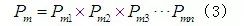
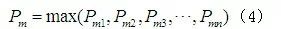


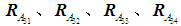 :
:
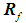 , and four experts are invited to score, with only one expert’s judgment matrix shown here:
, and four experts are invited to score, with only one expert’s judgment matrix shown here:
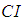 :
: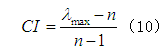
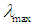 is the maximum eigenvalue of the matrix, and
is the maximum eigenvalue of the matrix, and 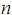 is the order of the matrix.
is the order of the matrix.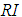 ,
, 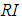 values are shown in Table 4.
values are shown in Table 4.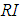
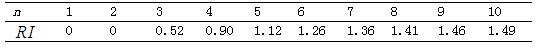
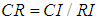 , when satisfying
, when satisfying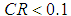 , it is considered that the judgment matrix meets the requirements; otherwise, adjustments are needed.
, it is considered that the judgment matrix meets the requirements; otherwise, adjustments are needed.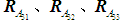 and
and 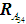 have maximum eigenvalues of 5.112, 5.024, 5.403, and 5.276, with the matrix order
have maximum eigenvalues of 5.112, 5.024, 5.403, and 5.276, with the matrix order 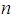 being 5, and
being 5, and 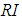 according to Table 4 is 1.12. The consistency ratios calculated are
according to Table 4 is 1.12. The consistency ratios calculated are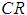 of 0.025, 0.005, 0.089, and 0.061, satisfying the consistency testing requirements. The same method is used to test the remaining matrices; if they do not meet the requirements, adjustments are made, ultimately obtaining all judgment matrices.
of 0.025, 0.005, 0.089, and 0.061, satisfying the consistency testing requirements. The same method is used to test the remaining matrices; if they do not meet the requirements, adjustments are made, ultimately obtaining all judgment matrices.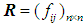 , using formulas (11) and (12) to complete the fuzzification process. After obtaining the fuzzy consistent matrix, the weights of the indicators in the evaluation layer (such as the denial of service indicator
, using formulas (11) and (12) to complete the fuzzification process. After obtaining the fuzzy consistent matrix, the weights of the indicators in the evaluation layer (such as the denial of service indicator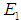 ) against the element layer system devices (such as the OPC server
) against the element layer system devices (such as the OPC server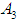 ) can be calculated.
) can be calculated.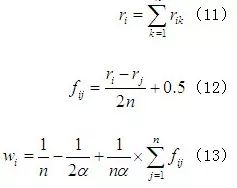
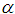 satisfy
satisfy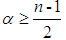 , and are inversely proportional to the differences in weights, meaning that when
, and are inversely proportional to the differences in weights, meaning that when 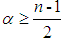 reaches its maximum, the differences in relative weights of each risk factor are maximized. In this example, n=5, leading to
reaches its maximum, the differences in relative weights of each risk factor are maximized. In this example, n=5, leading to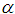 =2. The obtained judgment matrices, and their fuzzification, will lead to fuzzy consistent matrices
=2. The obtained judgment matrices, and their fuzzification, will lead to fuzzy consistent matrices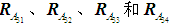 . Taking the fuzzy judgment matrix from the first expert
. Taking the fuzzy judgment matrix from the first expert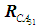 , the relative weight of the OPC server can be calculated.
, the relative weight of the OPC server can be calculated.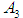 Similarly, the relative weights of the other four attack methods on the OPC server can be obtained, leading to the weight vector of the five attack indicators on the OPC server
Similarly, the relative weights of the other four attack methods on the OPC server can be obtained, leading to the weight vector of the five attack indicators on the OPC server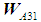 =[0.162,0.145,0.234,0.191,0.268]. Following the same approach, the weight vectors for the other three experts’ fuzzy judgment matrices
=[0.162,0.145,0.234,0.191,0.268]. Following the same approach, the weight vectors for the other three experts’ fuzzy judgment matrices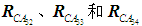 lead to the weight vectors of the five attack indicators on the OPC server as follows:
lead to the weight vectors of the five attack indicators on the OPC server as follows:
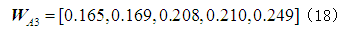
 can be calculated:
can be calculated: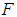

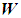 , with the entire calculation process shown in Table 5.
, with the entire calculation process shown in Table 5.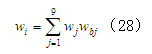
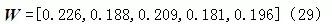
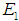 denial of service and
denial of service and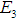 data tampering. An attack tree model is established for the five attack methods to quantitatively analyze the probability of each attack method occurring.
data tampering. An attack tree model is established for the five attack methods to quantitatively analyze the probability of each attack method occurring.
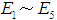 represents the five attack methods,
represents the five attack methods,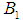 represents the attack cost, attack difficulty, and the possibility of being discovered. Taking data tampering
represents the attack cost, attack difficulty, and the possibility of being discovered. Taking data tampering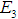 as an example, from the attacker’s perspective, they would prefer that this data tampering attack is not easily detected, giving it a greater weight than attack cost and difficulty. Increasing the attack difficulty will reduce the probability of the entire attack event, and its weight is slightly lower compared to attack cost.
as an example, from the attacker’s perspective, they would prefer that this data tampering attack is not easily detected, giving it a greater weight than attack cost and difficulty. Increasing the attack difficulty will reduce the probability of the entire attack event, and its weight is slightly lower compared to attack cost.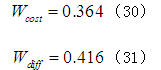
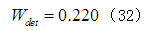
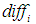 , attack cost
, attack cost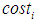 , and the possibility of being discovered
, and the possibility of being discovered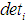 scoring standards, as shown in Table 6.
scoring standards, as shown in Table 6.
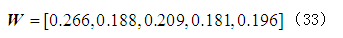
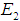 eavesdropping attacks and
eavesdropping attacks and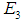 data tampering, thus emphasizing the need to strengthen prevention against eavesdropping attacks and data tampering.
data tampering, thus emphasizing the need to strengthen prevention against eavesdropping attacks and data tampering.
