✅ Author Profile: A Matlab simulation developer passionate about research, skilled in data processing, modeling simulation, program design, complete code acquisition, paper reproduction, and scientific simulation.
🍎 Previous reviews, follow the personal homepage: Matlab Research Studio
🍊 Personal motto: Investigate to gain knowledge, complete Matlab code and simulation consultation available via private message.
🔥 Content Introduction
1. Research Background
In the field of digital signal processing, with the continuous development of technology, in-depth research on signal characteristics has become increasingly important. Chaos signals, characterized by nonlinearity, non-periodicity, and high sensitivity to initial conditions, are widely present in various fields such as physics, biology, and communications. For example, in communication systems, chaos signals can be used for secure communication, enhancing the security of information transmission through their complex characteristics; in biomedical fields, chaotic characteristics may also be present in biological electrical signals, and studying them can aid in disease diagnosis and treatment. Complexity, as a key indicator describing the irregularity and uncertainty of chaos signals, allows for a deeper understanding of the intrinsic structure and dynamic behavior of chaos signals, providing important theoretical support and technical means for tasks such as signal analysis, feature extraction, and signal generation in digital signal processing.
2. Concepts of Chaos Signals and Complexity
2.1 Basic Characteristics of Chaos Signals
Chaos signals exhibit unique dynamic characteristics. Their most significant feature is extreme sensitivity to initial conditions, meaning that even slight changes in initial conditions can lead to significant differences in signal trajectories over time, a phenomenon known as the “butterfly effect.” Additionally, although chaos signals display irregular, seemingly random behavior, they are not truly random signals; rather, they are generated by deterministic nonlinear systems, possessing inherent regularity and structure. From a spectral perspective, the spectrum of chaos signals is continuous and covers a wide frequency range, which is distinctly different from periodic signals and typical random signals.
2.2 Concept of Complexity
Complexity is a concept used to quantify the degree of irregularity and uncertainty in a signal, reflecting the amount of information and the complexity of the structure contained within the signal. For chaos signals, measuring complexity helps distinguish signals generated by different chaotic systems and analyze the variations of chaos signals under different conditions. Various methods for measuring complexity describe the complex characteristics of signals from different perspectives, with common methods including approximate entropy, sample entropy, permutation entropy, and fuzzy entropy, each with its unique principles and applicable scenarios.
3. Measurement Methods for Chaos Signal Complexity
3.1 Approximate Entropy (ApEn)
Approximate entropy was proposed by Pincus in 1991 and is based on statistical pattern matching of time series. The basic idea is to measure the complexity of a signal by comparing the similarity of subsequences of lengths and within the time series. In the specific calculation process, the time series is first reconstructed into phase space, and then the similarity probability of subsequences of length with other subsequences is calculated under a given tolerance , leading to the approximate entropy value. A larger approximate entropy value indicates higher signal complexity, meaning more new patterns are contained within the signal. However, approximate entropy has certain limitations, such as high requirements for data length and lack of strict symmetry.
3.2 Sample Entropy (SampEn)
Sample entropy is an improved version of approximate entropy, proposed by Richman and Moorman in 2000. Compared to approximate entropy, sample entropy avoids the self-matching problem during calculation, offering better statistical performance and noise resistance. Sample entropy is also based on phase space reconstruction, measuring complexity by calculating the similarity probability of subsequences of lengths and , but the calculation method is simpler and more accurate. A larger sample entropy value indicates higher signal complexity, demonstrating good performance in analyzing subtle changes in chaos signals and distinguishing signals with different chaotic characteristics.
3.3 Permutation Entropy (PE)
Permutation entropy is based on the permutation patterns of time series. It arranges consecutive data points in the time series in order of size to obtain different permutation patterns, then counts the probabilities of various permutation patterns occurring, calculating the permutation entropy value from these probabilities. Permutation entropy reflects the degree of order in the data of the time series; a higher entropy value indicates higher signal complexity, meaning the data’s permutation patterns are more random. The calculation of permutation entropy is straightforward and sensitive to dynamic changes in signals, making it suitable for quickly detecting changes and anomalies in chaos signals.
3.4 Fuzzy Entropy (FuzzyEn)
Fuzzy entropy combines fuzzy theory and sample entropy concepts, measuring the similarity between subsequences of time series by introducing fuzzy membership functions. In the calculation process, fuzzy membership functions replace traditional distance measures, allowing for more accurate capture of the nonlinear features and complex structures of signals. Fuzzy entropy has less dependence on data length and exhibits good stability when processing noisy signals, making it widely used in the analysis of chaos signal complexity.
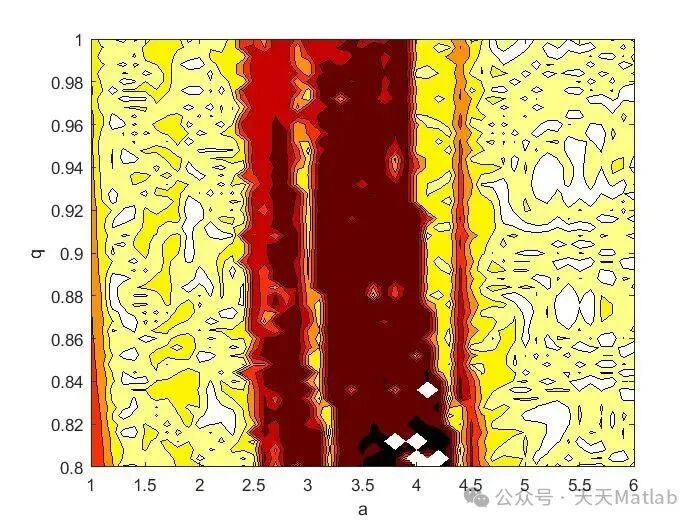
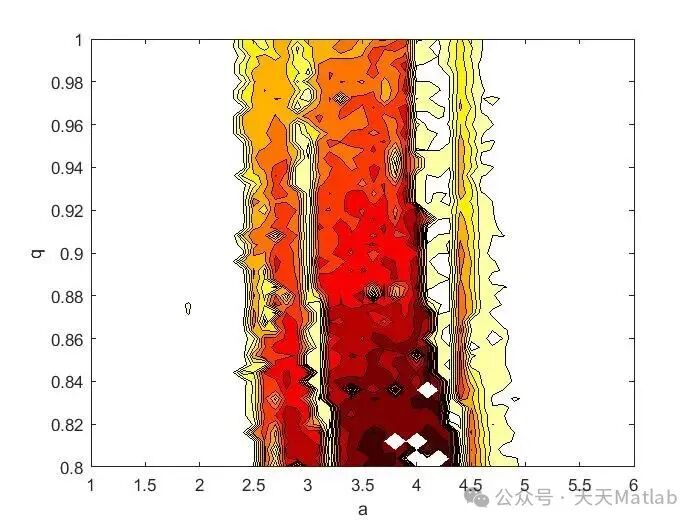
⛳️ Running Results
📣 Some Code
🔗 References
🎈 Some theoretical references are from online literature; if there is any infringement, please contact the author for removal.
👇 Follow me to receive a wealth of Matlab e-books and mathematical modeling materials.
🏆 Our team specializes in guiding customized MATLAB simulations in various research fields, helping to realize research dreams:
🌈 Various intelligent optimization algorithm improvements and applications
Production scheduling, economic scheduling, assembly line scheduling, charging optimization, workshop scheduling, departure optimization, reservoir scheduling, 3D packing, logistics site selection, cargo location optimization, bus scheduling optimization, charging pile layout optimization, workshop layout optimization, container ship loading optimization, pump combination optimization, medical resource allocation optimization, facility layout optimization, visual field base station and drone site selection optimization, knapsack problem, wind farm layout, time slot allocation optimization, optimal distributed generation unit allocation, multi-stage pipeline maintenance, factory-center-demand point three-level site selection problem, emergency supply material distribution center site selection, base station site selection, road lamp post arrangement, hub node deployment, transmission line typhoon monitoring devices, container scheduling, unit optimization, investment portfolio optimization, cloud server combination optimization, antenna linear array distribution optimization, CVRP problem, VRPPD problem, multi-center VRP problem, multi-layer network VRP problem, multi-center multi-vehicle VRP problem, dynamic VRP problem, two-layer vehicle routing planning (2E-VRP), electric vehicle routing planning (EVRP), hybrid vehicle routing planning, mixed flow shop problem, order splitting scheduling problem, bus scheduling optimization problem, flight shuttle vehicle scheduling problem, site selection path planning problem, port scheduling, port bridge scheduling, parking space allocation, airport flight scheduling, leak source localization.
🌈 Time series, regression, classification, clustering, and dimensionality reduction in machine learning and deep learning
2.1 BP time series, regression prediction, and classification
2.2 ENS voice neural network time series, regression prediction, and classification
2.3 SVM/CNN-SVM/LSSVM/RVM support vector machine series time series, regression prediction, and classification
2.4 CNN|TCN|GCN convolutional neural network series time series, regression prediction, and classification
2.5 ELM/KELM/RELM/DELM extreme learning machine series time series, regression prediction, and classification
2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU gated neural network time series, regression prediction, and classification
2.7 Elman recurrent neural network time series, regression prediction, and classification
2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM long short-term memory neural network series time series, regression prediction, and classification
2.9 RBF radial basis function neural network time series, regression prediction, and classification