✅ Author Profile: A Matlab simulation developer passionate about research, skilled in data processing, modeling simulation, program design, complete code acquisition, paper reproduction, and scientific simulation.
🍎 Previous reviews, follow the personal homepage:Matlab Research Studio
🍊 Personal motto: Seek knowledge through investigation, complete Matlab code and simulation consultation available via private message.
🔥 Content Introduction
1. Research Background
In the field of signal processing, Multivariate Variational Mode Decomposition (MVMD) is an advanced adaptive signal decomposition method that can decompose complex multivariate signals into multiple modal components with different characteristics. It has broad application prospects in various fields such as mechanical fault diagnosis, biomedical signal analysis, and financial time series processing. However, the MVMD algorithm faces challenges in determining parameters during practical applications, as the choice of decomposition parameters significantly impacts the accuracy and effectiveness of the decomposition results. Inappropriate parameter settings may lead to modal aliasing, over-decomposition, or under-decomposition, thereby reducing the quality of signal decomposition.
The Particle Swarm Optimization (PSO) algorithm is a global optimization algorithm based on swarm intelligence, which simulates the foraging behavior of birds to search for optimal solutions in the solution space. Applying the PSO algorithm to optimize MVMD parameters can fully leverage its global search capability, automatically finding the best parameter combinations for MVMD, improving the accuracy and reliability of signal decomposition, and providing a better data foundation for subsequent analysis and decision-making based on signal decomposition.
2. Core Technical Principles
2.1 Particle Swarm Optimization Algorithm (PSO)
In the PSO algorithm, each particle represents a potential solution to the problem and moves in a multidimensional solution space. During each iteration, particles adjust their velocity and position based on their own historical best position (Pbest) and the group’s historical best position (Gbest). The velocity update formula is:
[Insert PSO velocity update formula here]2.2 Multivariate Variational Mode Decomposition (MVMD)
MVMD is developed based on Variational Mode Decomposition (VMD) for processing multivariate signals. Its core idea is to decompose multivariate signals into multiple modal components by constructing and solving a variational model. In MVMD, each modal component has a corresponding center frequency and bandwidth. By optimizing the variational model, the sum of the estimated bandwidths of each modal component is minimized while ensuring that the sum of all modal components can accurately reconstruct the original signal.
Specifically, MVMD transforms the multivariate signal decomposition problem into a constrained variational problem. By introducing a quadratic penalty term and Lagrange multipliers, the constrained variational problem is converted into an unconstrained variational problem, which is iteratively solved using the Alternating Direction Method of Multipliers (ADMM) to obtain each modal component and its corresponding center frequency.
3. The Process of PSO Optimizing MVMD
3.1 Determining Optimization Parameters and Objective Function
In PSO-MVMD, it is necessary to determine the key parameters of MVMD as optimization variables for the PSO algorithm, such as the number of modes to be decomposed
Kand others. The design of the objective function is crucial for optimization, typically based on the rationality and effectiveness of each modal component after signal decomposition. For example, the sum of the kurtosis of each modal component after decomposition can be chosen as the objective function, as kurtosis reflects the impact characteristics of the signal. The larger the sum of kurtosis, the more effectively the modal components extract the impact features from the signal, indicating better decomposition results. The expression for the objective function is:
[Insert objective function expression here]⛳️ Running Results
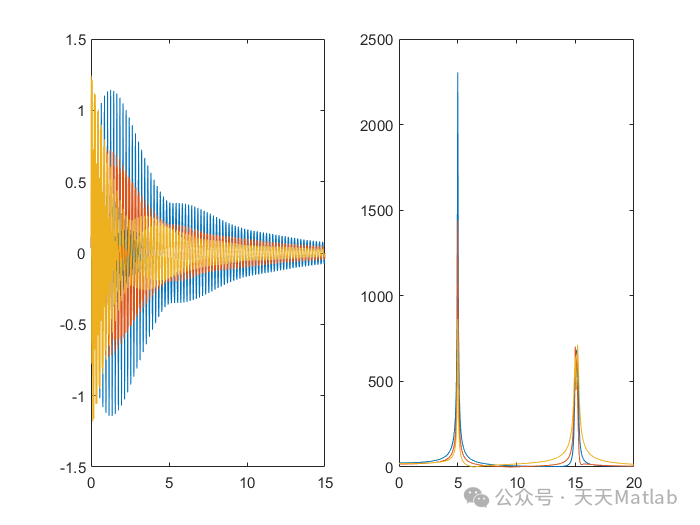
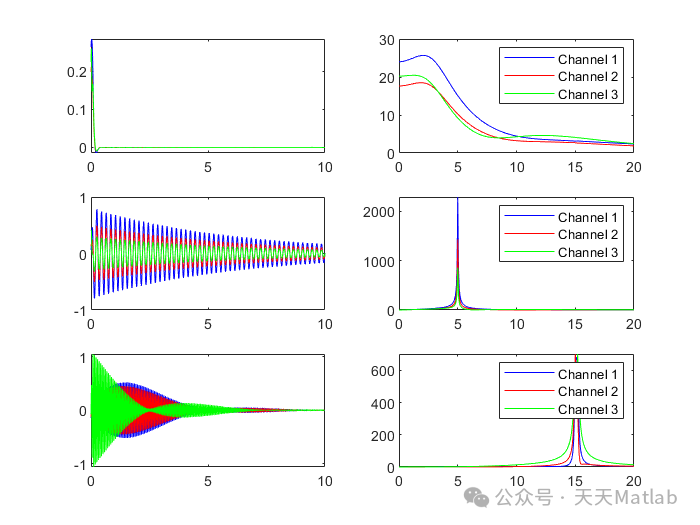
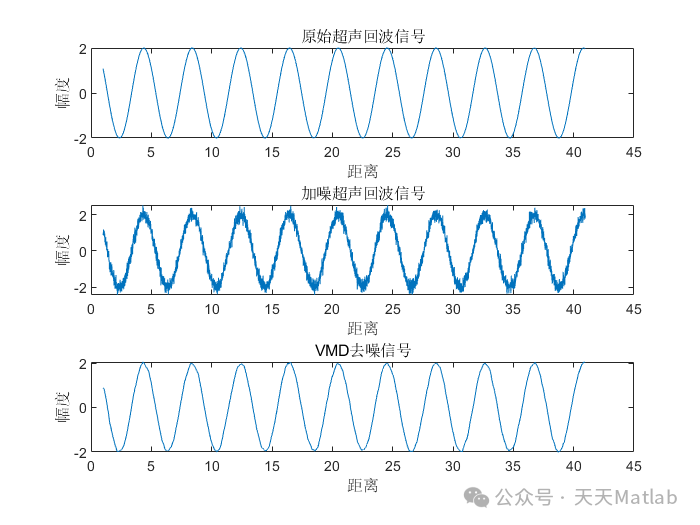
📣 Sample Code
🔗 References
🎈 Some theoretical references are from online literature; if there is any infringement, please contact the author for removal.
👇 Follow me to receive a wealth of Matlab e-books and mathematical modeling materials
🏆 Our team specializes in guiding customized Matlab simulations in various research fields, helping to realize research dreams:
🌈 Improvements and applications of various intelligent optimization algorithms
Production scheduling, economic scheduling, assembly line scheduling, charging optimization, workshop scheduling, departure optimization, reservoir scheduling, three-dimensional packing, logistics site selection, cargo position optimization, bus scheduling optimization, charging pile layout optimization, workshop layout optimization, container ship loading optimization, pump combination optimization, medical resource allocation optimization, facility layout optimization, visual domain base station and drone site selection optimization, knapsack problem, wind farm layout, time slot allocation optimization, optimal distributed generation unit allocation, multi-stage pipeline maintenance, factory-center-demand point three-level site selection problem, emergency supply distribution center site selection, base station site selection, road lamp arrangement, hub node deployment, transmission line typhoon monitoring devices, container scheduling, unit optimization, investment optimization portfolio, cloud server combination optimization, antenna linear array distribution optimization, CVRP problem, VRPPD problem, multi-center VRP problem, multi-layer network VRP problem, multi-center multi-vehicle VRP problem, dynamic VRP problem, two-layer vehicle routing planning (2E-VRP), electric vehicle routing planning (EVRP), hybrid vehicle routing planning, mixed flow shop problem, order splitting scheduling problem, bus scheduling optimization problem, flight shuttle vehicle scheduling problem, site selection path planning problem, port scheduling, port bridge scheduling, parking space allocation, airport flight scheduling, leak source localization
🌈 Time series, regression, classification, clustering, and dimensionality reduction in machine learning and deep learning
2.1 BP time series, regression prediction, and classification
2.2 ENS voice neural network time series, regression prediction, and classification
2.3 SVM/CNN-SVM/LSSVM/RVM support vector machine series time series, regression prediction, and classification
2.4 CNN|TCN|GCN convolutional neural network series time series, regression prediction, and classification
2.5 ELM/KELM/RELM/DELM extreme learning machine series time series, regression prediction, and classification
2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU gated neural network time series, regression prediction, and classification
2.7 Elman recurrent neural network time series, regression prediction, and classification
2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM long short-term memory neural network series time series, regression prediction, and classification
2.9 RBF radial basis function neural network time series, regression prediction, and classification