Understanding the Mysterious DES Encryption Algorithm

1 Introduction

DES algorithm is a common block cipher algorithm proposed by IBM in 1971. The DES algorithm is a typical representative of block ciphers and is also the most widely used symmetric encryption algorithm. This article will detail the principles and implementation process of DES.

1.1 Plaintext

Plaintext refers to data that has not been encrypted. Generally, plaintext is data waiting to be transmitted. Since plaintext has not been encrypted, it is easily recognizable and can be cracked, therefore it must be encrypted before transmission.

1.2 Ciphertext

Ciphertext is data obtained from plaintext after applying a certain encryption algorithm, usually in a complex and difficult-to-recognize format.

1.3 Key

A key is a parameter that is input into the algorithm when converting plaintext to ciphertext or vice versa.

1.4 Symmetric Encryption

Both parties in communication possess the same key; encryption and decryption are performed using the same key (i.e., the encryption key is equal to the decryption key, and the keys can be derived from each other). Before communication, both parties agree on a key which is not disclosed to third parties.

1.5 Block Cipher

A block cipher divides plaintext into fixed-length blocks, each block is encrypted using the same key and algorithm, and the output is also fixed-length ciphertext.

2 DES Encryption Algorithm

2.1 Block Length

In the DES encryption algorithm, both plaintext and ciphertext are 64-bit blocks. The key length is 64 bits, but each 8th bit of the key is used for parity, thus the actual key length is 56 bits.

2.2 Encryption Process

The DES encryption algorithm is roughly divided into four steps: (1) Initial Permutation, (2) Key Generation, (3) Iteration Process, (4) Inverse Permutation

Flowchart of the entire process:

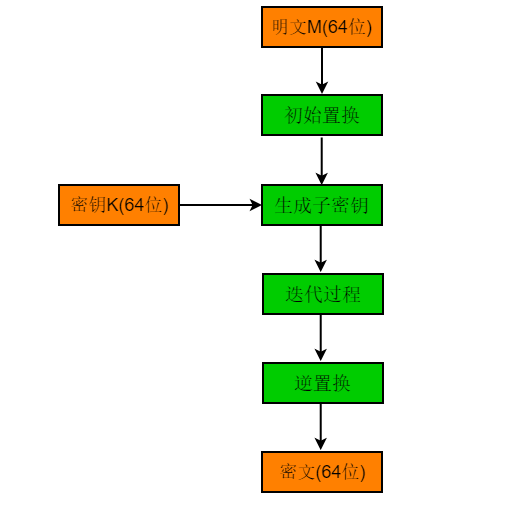
Encryption Process

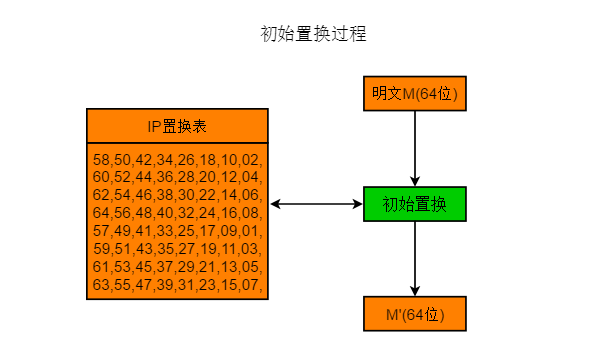
3 Initial Permutation

The initial permutation processes the original plaintext through the IP permutation table. The permutation process is shown in the figure:

For example, input 64-bit plaintext data M (64 bits): Plaintext M (64 bits) = 0110001101101111011011010111000001110101011101000110010101110010 select key K (64 bits): Key K (64 bits) = 0001001100110100010101110111100110011011101111001101111111110001

IP Permutation Table:

58,50,42,34,26,18,10,02,60,52,44,36,28,20,12,04,62,54,46,38,30,22,14,06,64,56,48,40,32,24,16,08,57,49,41,33,25,17,09,01,59,51,43,35,27,19,11,03,61,53,45,37,29,21,13,05,63,55,47,39,31,23,15,07,

The data in the IP permutation table indicates positions, for example, 58 indicates placing the 58th bit of M at the 1st position.

M after IP permutation becomes M’

M’ (64 bits) = 1111111110111000011101100101011100000000111111110000011010000011 take the first 32 bits of M’ as L0, thus L0 (32 bits) = 11111111101110000111011001010111 take the last 32 bits of M’ as R0, thus R0 (32 bits) = 00000000111111110000011010000011

4 Key Generation

The DES encryption performs 16 iterations, with each iteration processing data of 48 bits, thus requiring 16 keys of 48 bits for encryption. The process of generating sub-keys is as follows:

Using the example from section 3 to explain the calculation process of the sub-key:

(1) First Round Permutation:

Key K = 0001001100110100010101110111100110011011101111001101111111110001 needs to undergo PC-1 table permutation, i.e., execute the permutation selection 1 process. The PC-1 table is:

57,49,41,33,25,17,09,01,58,50,42,34,26,18,10,02,59,51,43,35,27,19,11,03,60,52,44,36,63,55,47,39,31,23,15,07,62,54,46,38,30,22,14,06,61,53,45,37,29,21,13,05,28,20,12,04

The PC-1 table is an 8-row by 7-column table; after PC-1, the key K becomes 56 bits of data K’.

K’ (56 bits) = 11110000110011001010101011110101010101100110011110001111 take the first 28 bits of K’ as C0, thus C0 (28 bits) = 1111000011001100101010101111 take the last 28 bits of K’ as D0, thus D0 (28 bits) = 0101010101100110011110001111

After obtaining C0 and D0, a left shift operation is performed, requiring reference to the shift table:

The left shift table for each round is as follows:

Round 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Shift Count 1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1

Performing the first round shift, the round count is 1, and the left shift count from the table is 1.

C0 left shift 1 bit becomes C1: C1 (28 bits) = 1110000110011001010101011111 D0 left shift 1 bit becomes D1: D1 (28 bits) = 1010101011001100111100011110 After merging C1 and D1, and undergoing PC-2 permutation, the sub-key K1 is obtained. The PC-2 table removes bits 9, 18, 22, 25, 35, 38, 43, and 54.

The PC-2 table is a 6X8 table, as follows:

14,17,11,24,01,05,03,28,15,06,21,10,23,19,12,04,26,08,16,07,27,20,13,02,41,52,31,37,47,55,30,40,51,45,33,48,44,49,39,56,34,53,46,42,50,36,29,32

After PC-2 permutation, the data becomes 48 bits, and the resulting key K1 is K1 (48 bits) = 000110110000001011101111111111000111000001110010

(2) Second Round Permutation

C1 and D1 are left shifted again, round count = 2, left shift count = 1, thus C1 and D1 left shift by 1 bit to obtain C2 and D2.

C2 (28 bits) = 1100001100110010101010111111 D2 (28 bits) = 0101010110011001111000111101 C2 and D2 merged become 56 bits, and after PC-2 permutation, the key K2 (48 bits) is obtained K2 (48 bits) = 011110011010111011011001110110111100100111100101. Proceeding in this manner, sub-keys K3-K16 are derived, noting the left shift counts for Ci and Di.

C3 (28 bits) = 0000110011001010101011111111 D3 (28 bits) = 0101011001100111100011110101 K3 (48 bits) = 010101011111110010001010010000101100111110011001

C4 (28 bits) = 0011001100101010101111111100 D4 (28 bits) = 0101100110011110001111010101 K4 (48 bits) = 011100101010110111010110110110110011010100011101

C5 (28 bits) = 1100110010101010111111110000 D5 (28 bits) = 0110011001111000111101010101 K5 (48 bits) = 011111001110110000000111111010110101001110101000

C6 (28 bits) = 0011001010101011111111000011 D6 (28 bits) = 1001100111100011110101010101 K6 (48 bits) = 011000111010010100111110010100000111101100101111

C7 (28 bits) = 1100101010101111111100001100 D7 (28 bits) = 0110011110001111010101010110 K7 (48 bits) = 111011001000010010110111111101100001100010111100

C8 (28 bits) = 0010101010111111110000110011 D8 (28 bits) = 1001111000111101010101011001 K8 (48 bits) = 111101111000101000111010110000010011101111111011

C9 (28 bits) = 0101010101111111100001100110 D9 (28 bits) = 0011110001111010101010110011 K9 (48 bits) = 111000001101101111101011111011011110011110000001

C10 (28 bits) = 0101010111111110000110011001 D10 (28 bits) = 1111000111101010101011001100 K10 (48 bits) = 101100011111001101000111101110100100011001001111

C11 (28 bits) = 0101011111111000011001100101 D11 (28 bits) = 1100011110101010101100110011 K11 (48 bits) = 001000010101111111010011110111101101001110000110

C12 (28 bits) = 0101111111100001100110010101 D12 (28 bits) = 0001111010101010110011001111 K12 (48 bits) = 011101010111000111110101100101000110011111101001

C13 (28 bits) = 0111111110000110011001010101 D13 (28 bits) = 0111101010101011001100111100 K13 (48 bits) = 100101111100010111010001111110101011101001000001

C14 (28 bits) = 1111111000011001100101010101 D14 (28 bits) = 1110101010101100110011110001 K14 (48 bits) = 010111110100001110110111111100101110011100111010

C15 (28 bits) = 1111100001100110010101010111 D15 (28 bits) = 1010101010110011001111000111 K15 (48 bits) = 101111111001000110001101001111010011111100001010

C16 (28 bits) = 1111000011001100101010101111 D16 (28 bits) = 0101010101100110011110001111 K16 (48 bits) = 110010110011110110001011000011100001011111110101

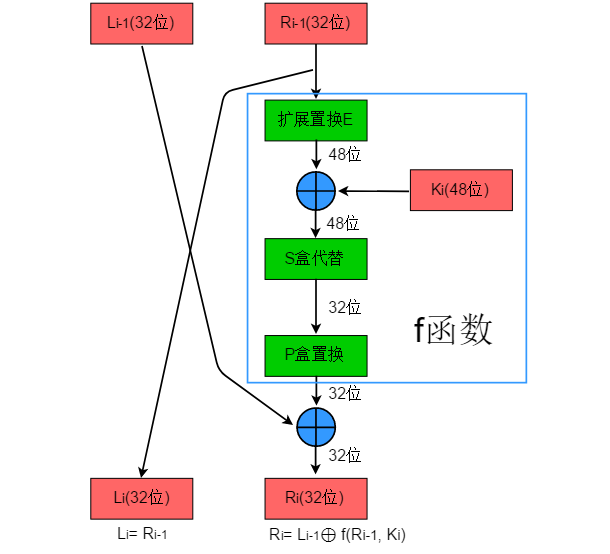
5 Iteration Process

Let Li (32 bits) and Ri (32 bits) be the left and right halves of the i-th iteration result, and Ki be the 48-bit encryption key for the i-th round. The operation rules are defined as follows:

Li = Ri-1; Ri = Li ⊕ f(Ri-1, Ki);

The entire iteration process is shown in the figure below:

5.1 Expansion Permutation E

The right half Ri has 32 bits, while the key Ki has 48 bits. To ensure that Ri can perform XOR operations with Ki, Ri’s bit count must be expanded, using the following expansion permutation table E:

Expansion Permutation Table E:

32,01,02,03,04,05,04,05,06,07,08,09,08,09,10,11,12,13,12,13,14,15,16,17,16,17,18,19,20,21,20,21,22,23,24,25,24,25,26,27,28,29,28,29,30,31,32,01

For example: L0 (32 bits) = 11111111101110000111011001010111 R0 (32 bits) = 00000000111111110000011010000011 R0 (32 bits) after expansion permutation becomes 48 bits of data: E(R0) (48 bits) = 100000000001011111111110100000001101010000000110

Perform XOR operation between E(R0) (48 bits) and K1 (48 bits)

100000000001011111111110100000001101010000000110 000110110000001011101111111111000111000001110010= 100110110001010100010001011111001010010001110100

Resulting: E(R0) ^ K1 (48 bits) = 100110110001010100010001011111001010010001110100

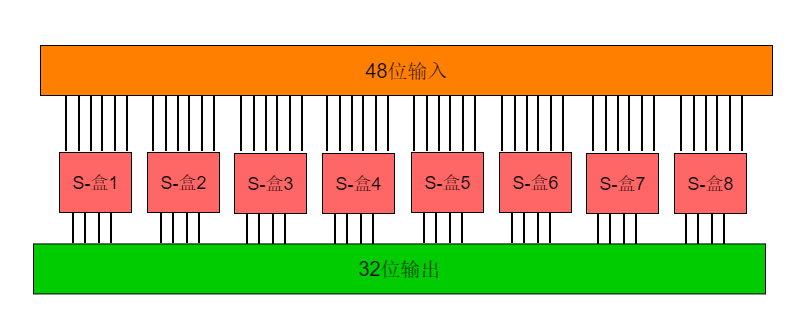
5.2 S-Box Substitution

The substitution operation is performed by 8 different substitution boxes (S-boxes). Each S-box has 6-bit input and 4-bit output. The substitution operation process is as follows:

S-Box 1:

14,04,13,01,02,15,11,08,03,10,06,12,05,09,00,07,00,15,07,04,14,02,13,01,10,06,12,11,09,05,03,08,04,01,14,08,13,06,02,11,15,12,09,07,03,10,05,00,15,12,08,02,04,09,01,07,05,11,03,14,10,00,06,13,

S-Box 2:

15,01,08,14,06,11,03,04,09,07,02,13,12,00,05,10,03,13,04,07,15,02,08,14,12,00,01,10,06,09,11,05,00,14,07,11,10,04,13,01,05,08,12,06,09,03,02,15,13,08,10,01,03,15,04,02,11,06,07,12,00,05,14,09,

S-Box 3:

10,00,09,14,06,03,15,05,01,13,12,07,11,04,02,08,13,07,00,09,03,04,06,10,02,08,05,14,12,11,15,01,13,06,04,09,08,15,03,00,11,01,02,12,05,10,14,07,01,10,13,00,06,09,08,07,04,15,14,03,11,05,02,12,

S-Box 4:

07,13,14,03,00,06,09,10,01,02,08,05,11,12,04,15,13,08,11,05,06,15,00,03,04,07,02,12,01,10,14,09,10,06,09,00,12,11,07,13,15,01,03,14,05,02,08,04,03,15,00,06,10,01,13,08,09,04,05,11,12,07,02,14,

S-Box 5:

02,12,04,01,07,10,11,06,08,05,03,15,13,00,14,09,14,11,02,12,04,07,13,01,05,00,15,10,03,09,08,06,04,02,01,11,10,13,07,08,15,09,12,05,06,03,00,14,11,08,12,07,01,14,02,13,06,15,00,09,10,04,05,03,

S-Box 6:

12,01,10,15,09,02,06,08,00,13,03,04,14,07,05,11,10,15,04,02,07,12,09,05,06,01,13,14,00,11,03,08,09,14,15,05,02,08,12,03,07,00,04,10,01,13,11,06,04,03,02,12,09,05,15,10,11,14,01,07,06,00,08,13,

S-Box 7:

04,11,02,14,15,00,08,13,03,12,09,07,05,10,06,01,13,00,11,07,04,09,01,10,14,03,05,12,02,15,08,06,01,04,11,13,12,03,07,14,10,15,06,08,00,05,09,02,06,11,13,08,01,04,10,07,09,05,00,15,14,02,03,12,

S-Box 8:

13,02,08,04,06,15,11,01,10,09,03,14,05,00,12,07,01,15,13,08,10,03,07,04,12,05,06,11,00,14,09,02,07,11,04,01,09,12,14,02,00,06,10,13,15,03,05,08,02,01,14,07,04,10,08,13,15,12,09,00,03,05,06,11,

Calculation Rule of S-Boxes: For example, if the input of S-Box 1 is 110111, the first and last bits form 11, the decimal value is 3, which corresponds to the 3rd row, and the middle 4 bits are 1011, corresponding to the decimal value 11, which corresponds to the 11th column. The value found in S-Box 1 is 14, so the output of S-Box 1 is 1110. The 8 S-boxes output 32 bits of data from the 48 bits input.

According to the calculation process of the S-box, the E(R0) ^ K1 (48 bits) = 100110110001010100010001011111001010010001110100, through S-box substitution, the output from the S-box is 10001011110001000110001011101010 (32 bits).

5.3 P-Box Permutation

The output result from the S-box substitution is used as input for the P-box permutation. The P-box permutation table is as follows:

16,07,20,21,29,12,28,17,01,15,23,26,05,18,31,10,02,08,24,14,32,27,03,09,19,13,30,06,22,11,04,25,

The output from the S-box 10001011110001000110001011101010 (32 bits) after P-box permutation is 01001000101111110101010110000001

Let Expansion Permutation E, S-Box Substitution, P-Box Permutation be the function f.

The first iteration process f(R0,K1) is: f(R0,K1) = 01001000101111110101010110000001

Calculate L1 (32 bits) = R0 = 00000000111111110000011010000011 Calculate R1 (32 bits) = L0 ^ f(R0,K1) 11111111101110000111011001010111 01001000101111110101010110000001 = 10110111000001110010001111010110

R1 (32 bits) = 10110111000001110010001111010110. Using L1 and R1 as inputs, continue executing the iteration process f until L16 and R16 are output.

After 16 iterations, the output is:

L16 (32 bits) = 00110000100001001101101100101000 R16 (32 bits) = 10110001011001010011000000011000

6 Inverse Permutation

After performing 16 rounds of iterative encryption on the initial permutation, obtaining L16 and R16, this input block undergoes inverse permutation to produce the final ciphertext output block. The inverse permutation is the inverse operation of the initial permutation. From the initial permutation rules, we can see that the original data’s 1st position is swapped to the 40th position, and the 2nd position is swapped to the 8th position. Thus, the inverse permutation swaps the 40th position back to the 1st position and the 8th position back to the 2nd position. The inverse permutation rules table is as follows:

40,08,48,16,56,24,64,32,39,07,47,15,55,23,63,31,38,06,46,14,54,22,62,30,37,05,45,13,53,21,61,29,36,04,44,12,52,20,60,28,35,03,43,11,51,19,59,27,34,02,42,10,50,18,58 26,33,01,41,09,49,17,57,25,

Inverse permutation process diagram:

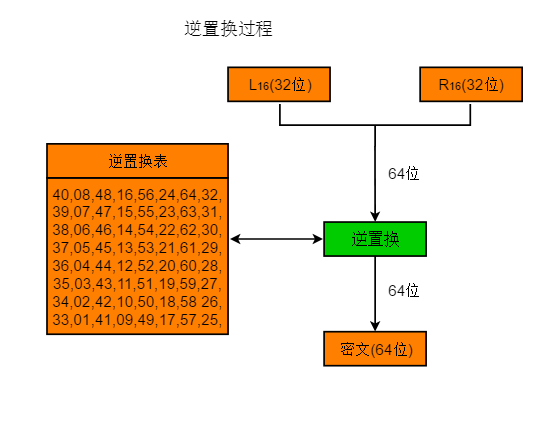
Combining L16 and R16 forms 64 bits of data, and after the inverse permutation table, the ciphertext output is:

Ciphertext: 0101100000001000001100000000101111001101110101100001100001101000

7 Conclusion

The DES encryption algorithm is the most common block cipher algorithm. Its main idea lies in the permutation and shift process of data bits, resulting in the final ciphertext through 16 rounds of iterative encryption and the final inverse permutation. The decryption method of DES can be solved by following the reverse process of encryption. Since the algorithm for the DES encryption process is public, the confidentiality of the key K becomes particularly important; only the sender and receiver using the same key for encryption and decryption can retrieve the plaintext data.