
Introduction
This article attempts to discuss the evolution of cryptographic algorithms from ancient to modern times, as well as the key cryptographic algorithms that have emerged throughout this process. Due to my limited knowledge, I hope for your guidance if there are any errors.
About Cryptographic Algorithms
At first glance, cryptographic algorithms may seem distant from most people’s daily lives, but they are actually closely related. From the network layer to the host file layer, every layer of encryption applications or protocols is supported by various cryptographic algorithms. Even if you do not use any encryption products, any website using HTTPS has already employed the encryption protocol TLS/SSL. You passively enjoy the privacy protection and communication security brought by cryptographic algorithms. Today, let’s delve into various interesting cryptographic algorithms beyond their superficial applications.
Before discussing cryptographic algorithms, let’s first clarify that the main purpose of a cryptographic algorithm is to transform plaintext into ciphertext. After encryption, plaintext becomes ciphertext, preventing information leakage. Although it may appear similar to gibberish, ciphertext is not gibberish. Most gibberish occurs due to inconsistent encoding. Encoding does not belong to cryptographic algorithms; it cannot transform plaintext into ciphertext but merely changes the display format. Therefore, Base64 is just an encoding method; it is not a cryptographic algorithm and does not have encryption capabilities, thus cannot guarantee the safety of your plaintext. So, if someone claims they use Base64 for encryption, it’s best to ignore them.
The adoption of cryptographic algorithms must meet the following three requirements:
-
Confidentiality:
Ensure that even if data is stolen, the thief cannot understand it;
-
Integrity:
Ensure that if data is intercepted and modified during transmission, the recipient can detect that the information has been captured and choose to discard it;
-
Availability:
Ensure that the overhead and complexity of the cryptographic algorithm are within a usable range.
Based on the above requirements, the development of cryptographic algorithms has mainly gone through two important periods: classical cryptography and modern cryptography.
I. How Did Ancient People Encrypt?
1. The Earliest Cryptographic Algorithms in History
Early cryptographic algorithms were primarily used in military contexts. The earliest recorded mention of cryptographic algorithms comes from the Zhou Dynasty’s military book “Six Secret Teachings” in the chapters “Yin Fu” and “Yin Shu.” It records:
Taigong said, “The lord and the general have Yin Fu, which comes in eight types. There is a symbol for great victories over enemies, one foot long. A symbol for breaking the army and capturing generals, nine inches long. A symbol for surrendering cities and gaining territories, eight inches long. A symbol for repelling enemies and reporting from afar, seven inches long. A symbol for asking for grain and increasing troops, five inches long. A symbol for defeated armies and lost generals, four inches long. A symbol for lost soldiers, three inches long. Those who serve as envoys must have their symbols recorded; if they delay and the symbols are leaked, all will be executed. The eight symbols are the secret messages of the lord and general, used for covert communication without revealing the techniques to the enemy. Even if the enemy is wise, they cannot recognize them.”
King Wu asked Taigong, “… Symbols cannot be clear; distances are far, and communication is not possible. What should we do?” Taigong said, “For serious matters, use writing, not symbols. The lord should send a letter to the general, and the general should ask the lord with a letter. The letters should be divided into three parts and sent separately. Only when all three parts are received can the message be understood. This is called Yin Shu. Even if the enemy is wise, they cannot recognize it.”
In simple terms, Yin Fu uses eight different lengths of symbols to convey different messages and commands, representing a substitution method in cryptography. In practice, it transforms information into symbols that the enemy cannot understand, while those in the know understand their meanings. This symbolic method cannot express rich meanings, only the eight critical meanings. Yin Shu, as a supplement to Yin Fu, uses a method of splitting text directly into three parts, sent through three different channels to the target. The enemy can only decipher the content of the Yin Shu if they capture all three parts simultaneously.
The simple idea of cryptographic algorithms mentioned above primarily employs substitution methods. Coincidentally, in distant Western history, cryptographic algorithms were also widely used in warfare. Herodotus recorded in his “Histories” that in the 5th century BC, Greek city-states and the Persian Empire engaged in multiple conflicts and wars. During these wars, the Greek city-states extensively employed shifting methods to encrypt military communication, making it difficult for the Persian Empire to obtain military intelligence from the Greek city-states and thus unable to make military deployments in advance.
The Greek city-states used fixed-length text to transmit military information and commands. The recipient would have a copy of the text’s shifting instructions. Upon receiving the ciphertext, the decryptor would use the shifting instructions to decrypt it, thus uncovering the military orders or messages.
2. The Evolution of Ancient Ciphers: The Caesar Cipher
Classical ciphers mainly employed shifting and substitution methods. Over time, the most famous of these is the Caesar cipher. The Caesar cipher has two modes—shifting and substitution. In the shifting mode, the plaintext is shifted a fixed number of positions in a specific direction. For example, “I love you” shifted right by four positions becomes “M pszi csy.” However, in English or Latin, the frequency of letters is not uniform. For instance, the letter ‘e’ appears much more frequently than others. After obtaining enough ciphertext samples, one can accurately find the shifting rule through frequency analysis, thereby decrypting the ciphertext. Moreover, due to the need for reversible operations, the number of keys is limited to only 25 possibilities. Therefore, it is entirely feasible to crack the ciphertext through brute force.
As a result, most Caesar ciphers in practical applications adopt the second mode—substitution. A mapping table for plaintext and ciphertext is defined.
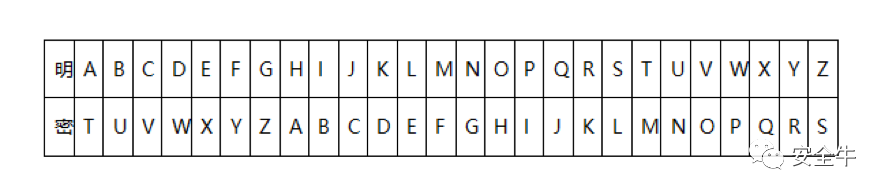
This method can somewhat alleviate the issue of exhaustive key search but remains vulnerable to large data frequency attacks.
Later, this mode evolved by introducing specific parameters to disrupt frequency patterns, which increased the difficulty of decryption but still fell within the categories of substitution and shifting methods.
Classical ciphers later developed into a series of ciphers including the Vigenère cipher, ROT5/13/18/47, Morse code, etc. However, they are all fundamentally based on substitution and shifting methods, and their security primarily relies on the algorithms not being publicly disclosed. The cryptographic algorithms used can only be considered the embryonic forms of today’s cryptographic algorithms or merely the initial cryptographic ideas that can be referenced.
II. Modern and More Scientific Cryptographic Algorithms
Classical cryptographic algorithms mainly focused on linguistic pattern changes. It wasn’t until the mid-20th century when Shannon published “A Mathematical Theory of Communication” that the focus of cryptographic algorithms shifted towards applied mathematics. Consequently, three important categories of cryptographic algorithms gradually emerged: asymmetric encryption, symmetric encryption, and hash algorithms. These three types of algorithms are often used in combination in real-world scenarios to achieve the best results.
1. Symmetric Encryption Algorithms
Symmetric encryption algorithms are among the most widely used cryptographic algorithms. Common symmetric encryption algorithms include DES, AES, 3DES, TDEA, Blowfish, RC5, IDEA, etc. The characteristic of symmetric encryption is that both parties involved in encryption and decryption use the same key. The exposure of the encryption algorithm itself does not affect security; the key is the key to security. Based on different principles, symmetric encryption can be broadly divided into stream encryption and block encryption.
-
Stream Encryption
Stream encryption is a type of symmetric encryption algorithm that encrypts plaintext character by character. The most famous algorithms in stream encryption are RC4 and GSM. Stream encryption algorithms are relatively simple; plaintext and keys undergo agreed operations bit by bit to obtain ciphertext.
The simplest model is XOR stream encryption, for example:

Due to the simplicity of stream encryption principles, its algorithm structure has weaknesses. If the key stream is reused multiple times, and partial plaintext is leaked, attackers can easily calculate the key. Additionally, since encryption is performed bit by bit, even if an attacker modifies the data, the original data structure remains intact, making it challenging for the receiver to detect changes. While stream encryption is a fast and efficient method, its security is relatively low, and it is not recommended for encrypting critical information.
-
Block Encryption
Block encryption is much more complex internally; each encryption block undergoes at least 16 rounds of operations. Representative algorithms include DES and AES. Currently, AES is recommended, while DES is no longer secure.
-
DES
DES is an earlier standard for symmetric encryption that was widely used at the time. As computer performance has continuously improved, brute-forcing DES has become increasingly easier. Thus, DES is no longer secure and has gradually been replaced by 3DES and AES over the past decade.
The core of DES consists of three steps: initial permutation, round function, and inverse permutation.
Initial Permutation: The 64-bit input data block is rearranged bit by bit, and the output is divided into L0 and R0, each 32 bits long. The permutation rule is to swap the 58th bit to the 1st position, the 50th bit to the 2nd position, and so on, with the last bit being the original 7th bit. L0 and R0 are the two parts after permutation output, with L0 being the left 32 bits of the output and R0 being the right 32 bits. The permutation rules are shown in the following table:
58,50,42,34,26,18,10,2,60,52,44,36,28,20,12,4,
62,54,46,38,30,22,14,6,64,56,48,40,32,24,16,8,
57,49,41,33,25,17,9,1,59,51,43,35,27,19,11,3,
61,53,45,37,29,21,13,5,63,55,47,39,31,23,15,7,
Round Function: DES uses a 56-bit key along with an additional 8-bit parity bit (the 8th bit of each group serves as the parity bit) to produce a maximum block size of 64 bits. This is an iterative block cipher that employs a technique called Feistel, where the encrypted text block is divided into two halves. A subkey is applied to one half using a cyclic function, and the output is XORed with the other half; then these two halves are swapped. This process continues, but the last iteration does not involve swapping.
Inverse Permutation: DES uses 16 rounds of cycles, employing XOR, permutation, substitution, and shifting operations. After 16 iterations, L16 and R16 are obtained, which are then subjected to inverse permutation, which is the reverse operation of the initial permutation, resulting in the ciphertext output. The decryption process is simply the reverse operation of the entire encryption process.
-
AES
AES was developed to replace the original DES and has been widely analyzed and proven secure worldwide. It is currently one of the most secure symmetric encryption algorithms. Over the last decade, AES has become one of the most popular algorithms in symmetric key encryption. Unlike its predecessor DES, AES uses a substitution-permutation network rather than a Feistel structure.
Most AES computations are performed in a special finite field, and the encryption process operates on a 4×4 byte matrix, known as the “state,” where the initial value is a plaintext block (each element in the matrix corresponds to a byte in the plaintext block). During encryption, each round of AES encryption (except the last round) consists of four steps:
AddRoundKey—Each byte in the matrix is XORed with the round key for that round; each subkey is generated by the key generation scheme.
SubBytes—Each byte is replaced with a corresponding byte using a nonlinear substitution function via a lookup table.
ShiftRows—Each row in the matrix is cyclically shifted.
MixColumns—This operation mixes the columns of the matrix. This step uses linear transformation to mix the four bytes of each column. The MixColumns step is omitted in the final encryption round, replaced by another AddRoundKey.
-
Encryption Modes
Both AES and DES support different encryption modes internally, and the security and efficiency of each mode vary significantly. Here, we will briefly introduce the two most common modes: ECB and CBC.
ECB mode has high encryption efficiency but low security, as shown in the diagram below:
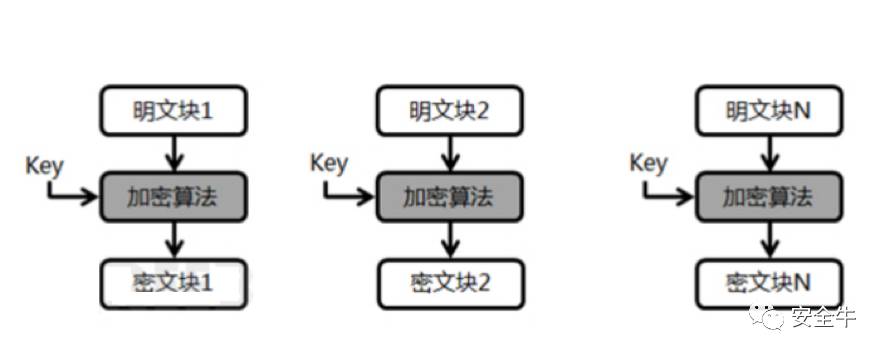
Each time, the key encrypts individual blocks, making it easy for opponents to crack. However, since there is no correlation between the modules, parallel processing can be used, greatly improving encryption efficiency. Typically, ECB encryption is 5-6 times more efficient than CBC.
Although CBC encryption is less efficient than ECB, its security is much higher. The mode is illustrated in the diagram below:
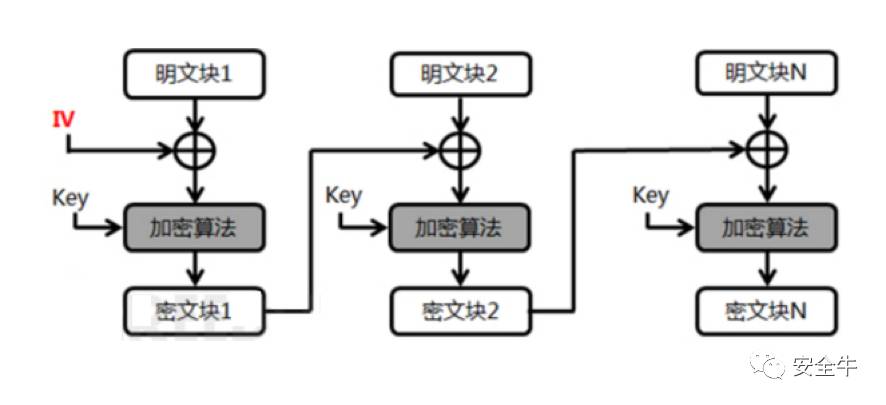
Each block of encryption introduces an IV that is different for each block and requires iteration from the previous block to complete the entire encryption process. Since each block’s IV is related to the ciphertext block, parallel processing cannot be used, and the entire process must be serial.
If high performance is not required, it is advisable to use CBC mode for encryption, as this mode is safer and more reliable.
2. Asymmetric Encryption Algorithms
The primary difference between asymmetric and symmetric encryption algorithms is that the encryption key and the decryption key are no longer the same. It is akin to two people using a secret code with each other. This method of encryption is mainly designed to address the “multiple encryptors, one decryptor” model, as symmetric keys can only resolve one-to-one decryption relationships.
Thus, in this many-to-one relationship, a public key system emerges. One public key corresponds to one private key. The public key is open, and any data sender uses the public key to encrypt data, but only the private key can unlock the contents encrypted with the public key. Notable algorithms include DSA, RSA, ElGamal, knapsack, Rabin, D-H, and ECC. The underlying mathematical principles range from large number factorization to complex discrete logarithm problems on elliptic curves, which are very complex. Here, I will not elaborate further.
Although the underlying mathematical support differs, the mode is similar; they all utilize public-private key pairs, where the public key decrypts information encrypted with the private key, and the private key decrypts information encrypted with the public key. The execution efficiency of asymmetric encryption algorithms becomes the biggest obstacle to their practical application. Most applications primarily use asymmetric encryption algorithms for identity verification and do not employ them for communication.
3. Hash Algorithms
Hash algorithms are also very common cryptographic algorithms. Unlike symmetric and asymmetric algorithms, they are not used for data transmission but rather for validating whether data has been tampered with, preventing malicious actors from modifying data. Their characteristic is that regardless of the length of the original text, they will transform into a fixed-length string, allowing only encryption and not decryption (one-way operation). For different inputs, they theoretically generate different outputs (some algorithms have already encountered large-scale collisions, which refer to different plaintext resulting in the same ciphertext).
Common hash algorithms include MD5, SHA-1, and SHA 224/256/512. Among these, MD5 and SHA-1 have been proven to be insecure, so it is recommended to use SHA256/512 and other high-security algorithms.
III. Database Encryption Algorithms
The aforementioned cryptographic algorithms have been widely applied across various fields. With the rapid development of cloud computing and big data, databases have gradually migrated from secure local area networks to private and even public clouds. In cloud environments, servers become less trustworthy, and as databases migrate to the cloud, they face more severe challenges, making data security in the cloud an unavoidable issue. Databases store critical data, and cloud hosts present numerous security risks, so encrypting databases in the cloud becomes a remedy for these security concerns.
1. Symmetric Encryption Algorithms
Database encryption differs from file encryption and communication encryption. Database encryption needs to pay special attention to whether the encryption algorithm has expansion properties and has strict performance requirements on the encryption algorithm. In 2009, during the development of database encryption products, the database security vendor Anhua Jinhe first excluded stream encryption algorithms from symmetric algorithms, as this method, while having inherent advantages in operational efficiency and solving data expansion, presents security issues under certain conditions. To pursue encryption efficiency, some domestic security vendors still use this method to provide database encryption services, neglecting the most basic security requirements of encryption products.
A more prudent approach is to use block encryption (AES) from symmetric encryption for related encryption processing. Block encryption has high security, providing better assurance in terms of safety, but it needs to solve the expansion issue caused by data block size limitations. This requires designing sufficiently sophisticated solutions based on specific situations or field requirements to address expansion issues for different fields or types, ultimately forming a perfect database encryption scheme.
2. Domestic Cryptographic Algorithms
Cryptographic algorithms are the core technology for ensuring information security, playing a crucial role in protecting national secrets and core data in various industries. Using internationally universal cryptographic algorithms and related standards such as 3DES, SHA-1, RSA poses significant security risks. Therefore, national authorities and regulatory agencies have proposed promoting the application of domestic cryptographic algorithms and strengthening industry security controls from the perspective of national security and long-term strategy. Currently, many domestic database encryption products prioritize supporting domestic cryptographic algorithms during user selection assessments, which is crucial for government, military, and confidentiality-related industries. Ensuring national information security must break free from excessive reliance on foreign technologies and products, with cryptographic algorithms as key security technologies needing to be domestically produced.
Specifically, domestic cryptographic algorithms (national cryptographic algorithms) refer to commercially recognized domestic cryptographic algorithms certified by the National Cryptography Administration. For example, in the financial sector, the publicly used SM2, SM3, and SM4 algorithms are primarily used, which correspond to asymmetric algorithms, hash algorithms, and symmetric algorithms, respectively.
Taking the SM4 algorithm as an example: The SM4 block cipher algorithm is a symmetric block cipher designed independently by China for implementing data encryption/decryption operations to ensure data and information confidentiality. A fundamental condition for ensuring the security of a symmetric cipher algorithm is that it possesses a sufficiently long key length. The SM4 algorithm has the same key length of 128 bits as the AES algorithm, thus providing higher security than the 3DES algorithm.
