
Click the blue text “ShunYun Multi-Physical Field Simulation”
Explore advanced algorithm engines
Elliptic Curve Cryptography (ECC) is a highly regarded topic. ECC is a public key encryption algorithm that utilizes points on an elliptic curve for encryption and decryption operations. Compared to traditional RSA algorithms, ECC offers greater efficiency and security by using shorter key lengths while maintaining the same level of security. ECC is widely used in resource-constrained environments such as mobile devices and the Internet of Things (IoT) because it provides equivalent security with reduced computational resources and storage space.
The Elliptic Curve Cryptography is based on the theory of elliptic curves. An elliptic curve is a set of points that satisfy a specific equation, and these points possess unique properties that can be used for encryption and decryption operations. The ECC algorithm ensures the security of encryption through the discrete logarithm problem of points on the elliptic curve, making it difficult to break even with more powerful computers.
In comparison to traditional RSA algorithms, the ECC algorithm requires shorter key lengths for the same level of security, which means it can provide higher efficiency and require less storage space. This is particularly important for mobile devices and IoT devices, which typically have limited computational resources and storage capacity. Therefore, the ECC algorithm has found extensive applications in these fields.
Overall, the Elliptic Curve Cryptography is an efficient and secure encryption algorithm that plays a crucial role in modern computing and communication systems. With the proliferation of mobile devices and IoT, the importance of the ECC algorithm will continue to grow, as it provides efficient and secure encryption solutions for these resource-constrained environments.
1. Elliptic Curve
In general, an elliptic curve can be represented by the following equation, where a, b, c, and d are coefficients.
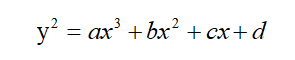
When a=1, b=0, c=-2, d=4, the resulting elliptic curve is:
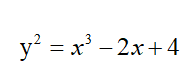
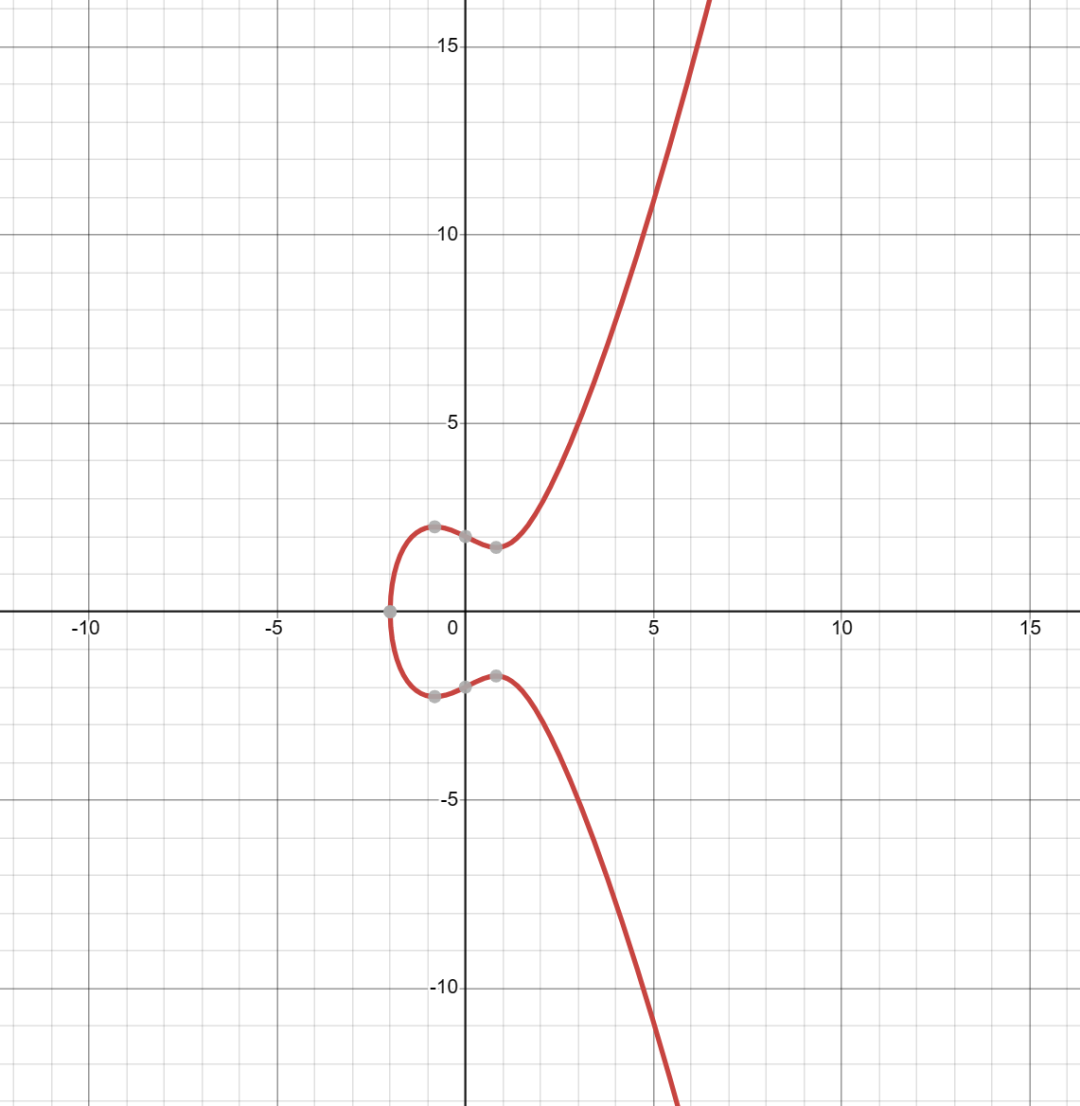
The graph of the elliptic curve E is shown below:
2. Operations on Elliptic Curves
The point operations on elliptic curves include two main rules: point addition and point multiplication.
On an elliptic curve, the addition operation between two points can be defined. Briefly, given two points P and Q, their sum P+Q can be obtained using the slope of the line through the two points on the elliptic curve. Additionally, a multiplication operation can be defined between two points; for example, given a point P and an integer k, the k-fold of point P can be obtained by performing point addition k times, usually denoted as kP. Point multiplication plays a crucial role in the elliptic curve encryption algorithm, used for generating public keys and in the calculations during encryption and decryption processes. These operational rules form the foundation of elliptic curve cryptography and constitute the core operations of the ECC algorithm.
3. Addition
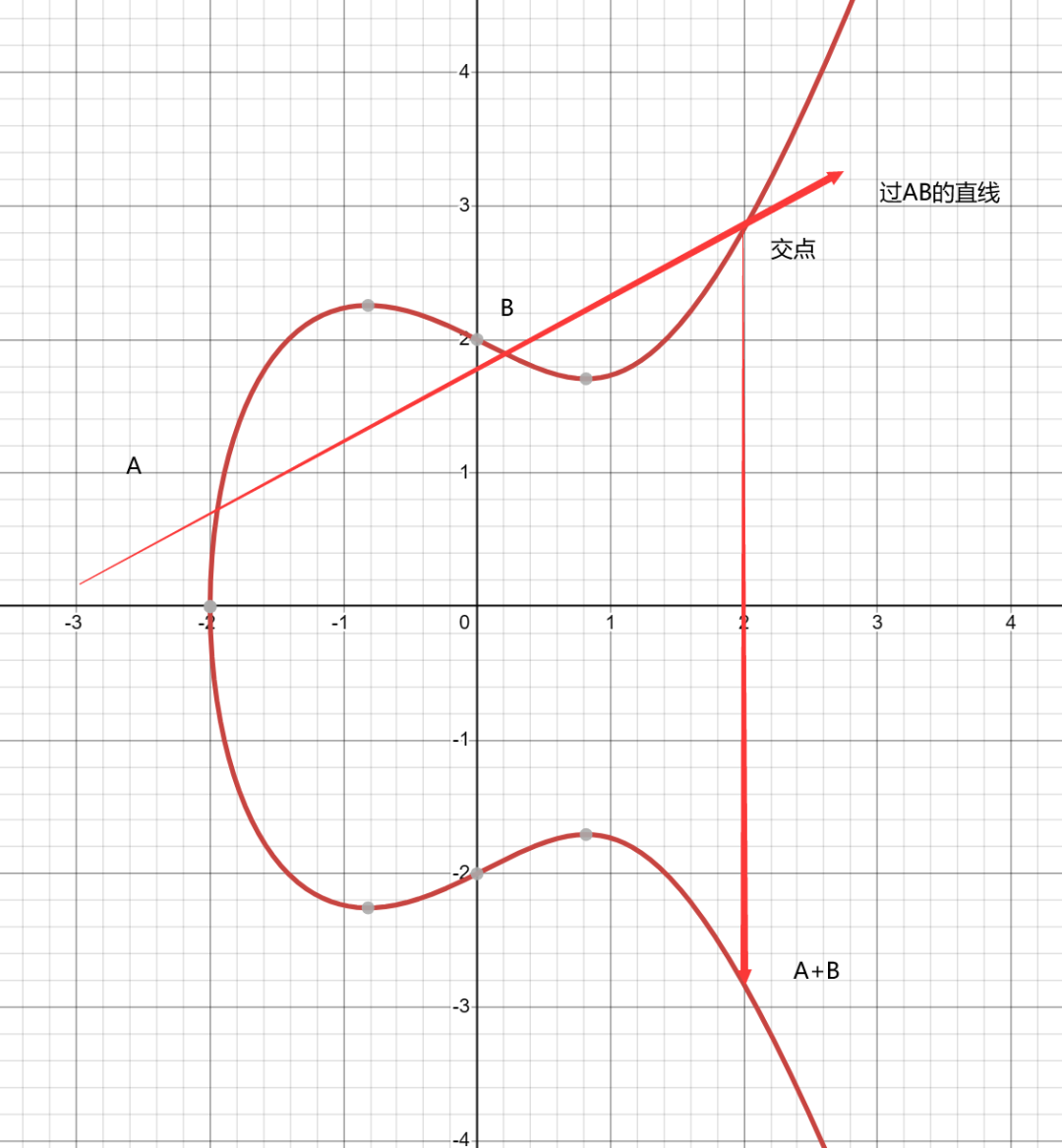
To add two points A and B on the curve, draw a line through points A and B, find the intersection points of the line with the elliptic curve, and the point symmetric to the intersection point about the x-axis is defined as A+B, which represents addition. As shown in the figure: A + B = C
4. Doubling Operation
The above method cannot explain the case of A + A, where the two points coincide. Therefore, in this case, the tangent at point A on the elliptic curve is drawn, and the intersection point of the tangent with the elliptic curve, symmetric to the intersection point about the x-axis, is defined as A + A, which is 2A, representing the doubling operation.
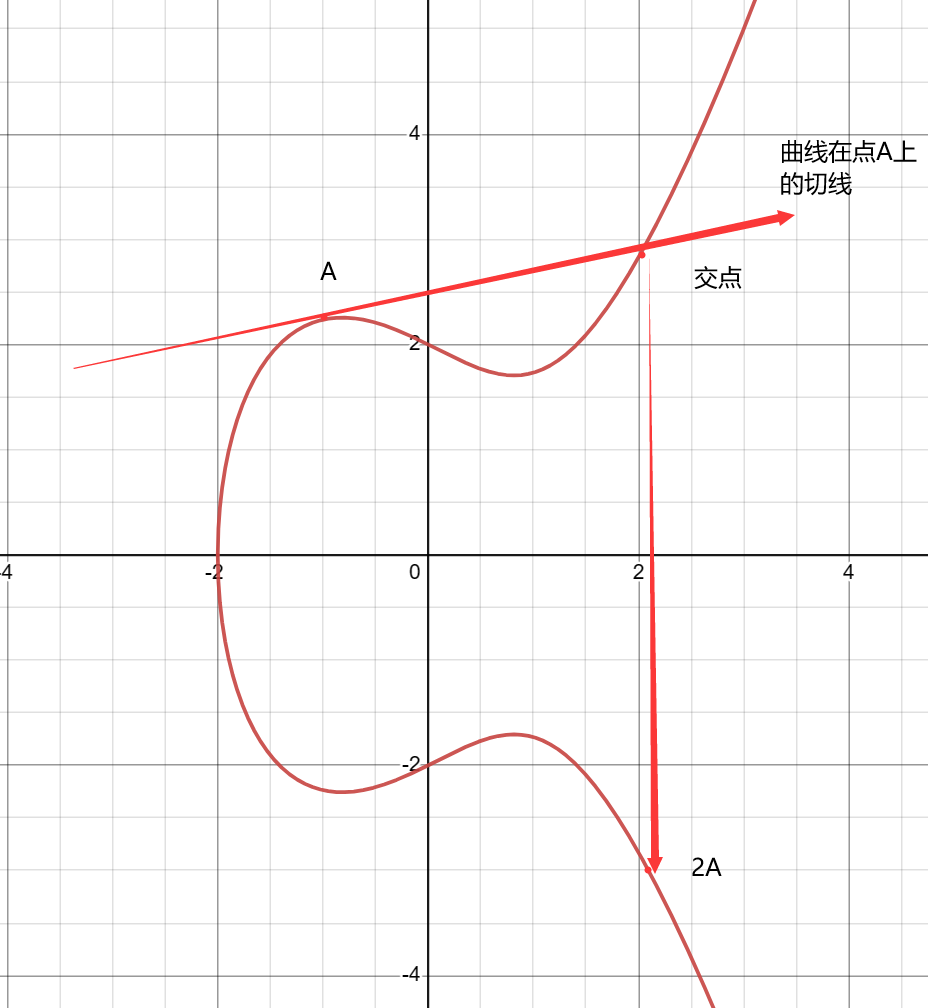
5. Negation
The point symmetric to A about the x-axis is defined as -A, which represents the negation operation on the elliptic curve. As shown in the figure:
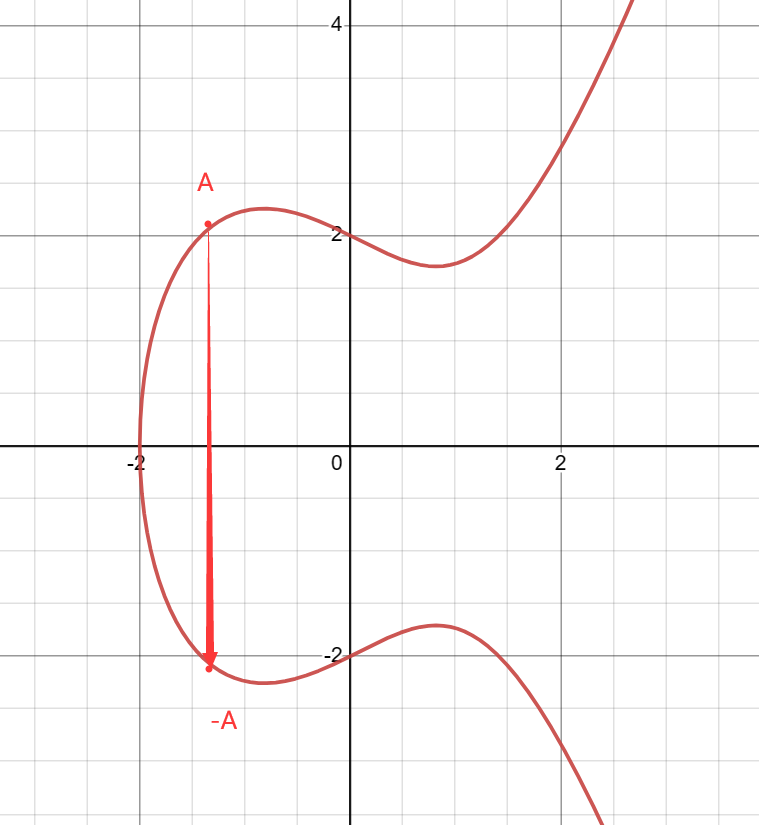
6. Point at Infinity
If A is added to -A, the line through A and -A parallel to the y-axis can be considered to intersect the elliptic curve at a point at infinity.
In summary, the definitions of A+B and 2A operations allow us to compute 2G, 3G (i.e., G + 2G), 4G, etc., given a point G on the elliptic curve. That is, when a point G is given, finding xG is not difficult. Conversely, given xG, finding x is very difficult. This is the mathematical principle behind the elliptic curve encryption algorithm.
7. Diffie-Hellman Key Exchange
The Diffie-Hellman key exchange is a secure key exchange protocol that allows two parties to negotiate a shared key without sharing their private keys. In this protocol, A and B can compute a common shared key using their respective private keys and each other’s public keys.
Specifically, A can use their private key a and point G of B to compute a value, denoted as A’s computed shared key K_A = aG. Similarly, B can use their private key b and A’s public key G to compute a value, denoted as B’s computed shared key K_B = bG. Due to mathematical properties, these two computed shared keys are the same, i.e., K_A = K_B.
Thus, A and B can compute a shared key for encrypting and decrypting their communication by exchanging public keys without revealing their private keys. The security of this protocol is based on the difficulty of the discrete logarithm problem, making it challenging for an attacker to derive the shared key from the public information.
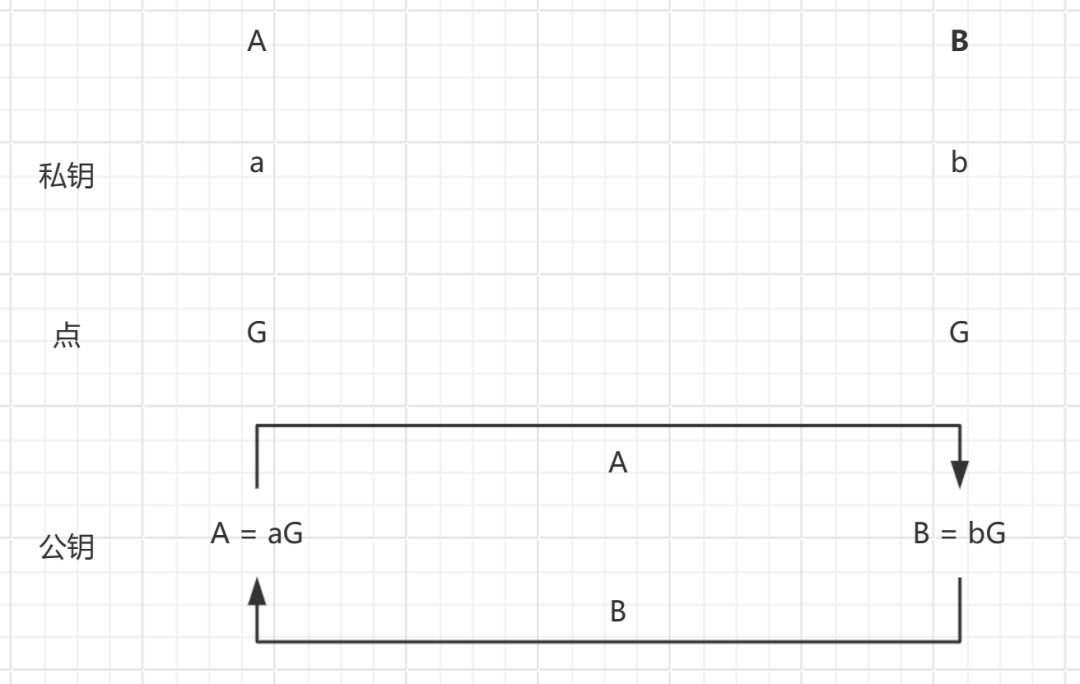
In the end, K_A = K_B, thus achieving the ability to decrypt the ciphertext sent to the other party using the public key, allowing them to read the information.
8. Encryption Process
The encryption process of the Elliptic Curve Cryptography includes the following steps:
1. Select an elliptic curve and a base point: First, choose an elliptic curve and a base point, where the order of the base point should be a large prime number.
2. Choose private and public keys: Next, select a private key, which is a random number less than the order of the base point. Then, compute the public key using the private key and the base point.
3. Encrypt the message: Convert the message to be encrypted into a point on the elliptic curve and select a random number as a parameter in the encryption process.
4. Calculate the encryption result: Use the public key, random number, and message point to compute the encryption result, which is typically a point on the elliptic curve.
5. Send the encryption result: Send the encryption result to the recipient.
After the recipient receives the encryption result, they can decrypt the message using their private key. The decryption process includes the following steps:
1. Use the private key to compute a value related to the random number used in the encryption process.
2. Use this value and the encryption result to compute the original message point.
3. Convert the message point back to the original message.
4. Through these steps, the recipient can successfully decrypt the encrypted message.
For these reasons, the Elliptic Curve Cryptography is considered secure under current computational capabilities and is difficult to break.

Development Engineer
Joy


Graduated in 2023 from Northeast Petroleum University with a major in Electronic Information Engineering, participated in the development of the ShunYun series software shonTA interface after joining the company.
Previous Highlights

Technical Sharing
shonFlow Flow Thermal Coupling Simulation Heat Sink Air Cooling

Technical Sharing
shonFlow Simulation Reveals Battery “Thermal Runaway”

Technical Sharing
Water Landing Simulation Based on shonDy

Technical Sharing
shonDy Software Simulates Vehicle Water Wading



Share

Collect

Like

View