This article introduces commonly used cryptographic algorithms in daily development.

Classical Cryptography

Classical cryptography typically employs simple techniques such as substitution (replacing letters in plaintext with other letters) and transposition (rearranging the order of letters in plaintext), without the need for complex machines or algorithms. Therefore, its security is insufficient and easily compromised.

• Caesar Cipher: This cipher shifts letters in the plaintext by a fixed number according to their order in the alphabet. The key space for this encryption method is very small, making it vulnerable to brute-force attacks.
• Simple Substitution Cipher: This cipher replaces plaintext letters with other letters based on a fixed one-to-one mapping. Due to the fixed one-to-one nature of the mapping, the frequency of letters in the plaintext corresponds to the frequency of letters in the ciphertext. Thus, when the ciphertext is sufficiently long, it can be broken through frequency analysis.

Modern Cryptography

Symmetric Encryption

Symmetric encryption refers to the use of the same key for both encryption and decryption. Because the processes for encryption and decryption are identical, symmetric encryption algorithms typically have high computational efficiency, making them suitable for scenarios involving large amounts of data.

DES Algorithm

The DES (Data Encryption Standard) algorithm is a symmetric encryption algorithm that uses a Feistel network. It is classified as a Block Cipher with a block length of 64 bits. Although the DES key length is 64 bits, the 8th bit of each byte is a parity bit, resulting in an effective key length of only 56 bits. Due to the short key length, the DES algorithm is no longer secure and can be compromised through brute-force attacks.

3DES (Triple Data Encryption Standard) is an encryption algorithm that applies the DES algorithm three times. The specific encryption process is as follows:

1. First encryption: Use key 1 to perform DES encryption on the plaintext.
2. Second encryption: Use key 2 to perform a decryption operation on the result from step 1.
3. Third encryption: Use key 3 to perform encryption on the result from step 2.

The reason for using a decryption operation in the second encryption step of the 3DES algorithm is to ensure backward compatibility with DES. If keys 1, 2, and 3 are all the same, 3DES degenerates into the DES algorithm. Additionally, if keys 1 and 3 are the same while key 2 is different, this variant of 3DES is called DES-EDE2; when all three keys are different, it is called DES-EDE3. Here, EDE stands for Encryption-Decryption-Encryption.

AES Algorithm

The AES (Advanced Encryption Standard) algorithm is also a symmetric encryption algorithm and is classified as a Block Cipher with a fixed block length of 128 bits. It supports key lengths of 128, 192, and 256 bits. This algorithm offers good security and is recommended for use.

Asymmetric Encryption

In asymmetric encryption, there are two types of keys: the encryption key and the decryption key. The encryption key is used for encryption, while the decryption key is required for decryption. Typically, the encryption key can be made public for senders to encrypt plaintext, hence it is also known as the Public Key; conversely, the decryption key must remain confidential and is held only by the recipient, thus referred to as the Private Key. The public and private keys are paired, meaning that ciphertext encrypted with a public key can only be decrypted with the corresponding private key, and vice versa. This pair of keys is known as a Key Pair. Although asymmetric encryption algorithms solve the key distribution problem, they are generally slower than symmetric encryption algorithms and are susceptible to man-in-the-middle attacks.

RSA Algorithm

Basic Principles

The RSA algorithm is a typical representative of asymmetric encryption and is currently a mainstream asymmetric encryption algorithm, recommended for use. Its plaintext, ciphertext, and keys are all numerical. The encryption process can be represented by the following formula: first, raise the plaintext to the power of e, then take the result modulo N to obtain the ciphertext. Here, e and N together form the public key, denoted as (N, e).

The decryption process can be represented by the following formula: first, raise the ciphertext to the power of d, then take the result modulo N to obtain the plaintext. Here, d and N together form the private key, typically denoted as (N, d).

The basic steps for generating the public and private keys in the RSA algorithm are as follows:

1. Select two large prime numbers: Use a pseudorandom number generator to select two sufficiently large and distinct random prime numbers p and q. The larger p and q are, the higher the security of the encryption.
2. Calculate N: N = p × q.
3. Calculate Euler’s totient function 𝜑(N). Since N is the product of two primes, it can be quickly calculated using the following formula:

1. Calculate e: Choose an integer e such that 1 < e < 𝜑(N) and e is coprime to 𝜑(N).
2. Calculate d: Find another integer d such that (d × e) mod 𝜑(N) = 1.

Choosing Private/Public Keys

Due to the nature of the RSA algorithm, the generated key pair key1 and key2 are equivalent, essentially because the values of e and d are interchangeable. In other words, ciphertext encrypted with key1 can be decrypted with key2, and vice versa. This raises the question: since the two generated keys are equivalent, can we arbitrarily choose one key to be made public as the public key and keep the other key secret as the private key?

Theoretically, this is possible, but in practice, it is not advisable.

• First, when using tools to generate RSA keys, we often find that the private key is significantly longer than the public key. This is because most tools include some original information from the key generation process in the private key. Clearly, if the private key is made public, it greatly increases the risk of the public key being guessed and compromised, significantly reducing security.
• Secondly, even if we assume that a certain tool generates a private key without original information, it is still not advisable to make it public. In theory, the value of e should be randomly selected during RSA key generation. However, in practice, to improve encryption efficiency, e is often fixed at small values like 3 or 65537. Because e is small, if we use (N, e) as the private key, it greatly increases the risk of brute-force attacks. The implementation of the RSA algorithm generally ensures that the value of d is large, making (N, d) a safer choice for the private key.

ECC Algorithm

The ECC (Elliptic Curve Cryptography) algorithm is an asymmetric encryption algorithm based on the elliptic curve discrete logarithm problem. Compared to the RSA algorithm, it can provide extremely high security with shorter key lengths, making it more efficient in computation and transmission, and very suitable for embedded devices and mobile devices. It is recommended for use.

ElGamal Algorithm

This is an asymmetric encryption algorithm based on the discrete logarithm problem, which can be used for data encryption, digital signatures, and other scenarios.

Hybrid Encryption Systems

The public key of asymmetric encryption algorithms can be made public, thus solving the key distribution problem of symmetric encryption algorithms. However, there are also drawbacks, as the speed of asymmetric encryption algorithms is far lower than that of symmetric encryption algorithms. Therefore, it is common to combine asymmetric and symmetric encryption algorithms to fully leverage the advantages of both, known as a hybrid encryption system. The specific encryption process is as follows:

1. The message sender generates a random key and then uses this key to encrypt the message with a symmetric encryption algorithm, resulting in the message ciphertext.
2. The message sender then uses the recipient’s public key to encrypt the key generated in step 1 with a asymmetric encryption algorithm, resulting in the ciphertext of the symmetric encryption algorithm’s key.
3. Combining the ciphertext of the symmetric encryption algorithm’s key and the message ciphertext results in the final ciphertext.

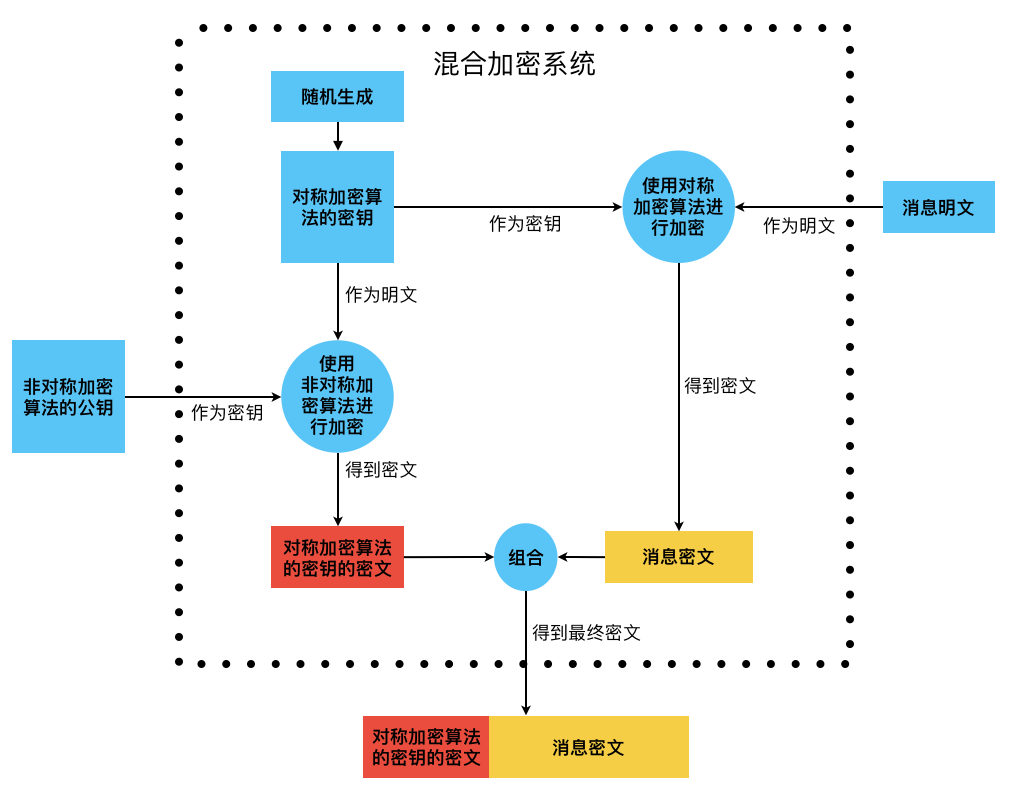
As for decryption, it is also straightforward:

1. Upon receiving the message, the recipient separates the ciphertext according to the agreed-upon message format, obtaining the ciphertext of the symmetric encryption algorithm’s key and the message ciphertext.
2. The recipient uses their private key to decrypt the ciphertext of the symmetric encryption algorithm’s key with the asymmetric encryption algorithm, obtaining the randomly generated symmetric encryption algorithm’s key from the sender.
3. The recipient then uses the symmetric encryption algorithm’s key obtained in step 2 to decrypt the message ciphertext with the symmetric encryption algorithm, ultimately retrieving the plaintext message.

References

1. Illustrated Cryptography Technology, 3rd Edition by Hiroshi Yuki