How Reference Voltage Noise Affects the LSB Size of ADCs and Ultimately Injects Output Errors

This is essentially the mathematical version of the previous article; I prefer a more serious approach.Review of ADC Encoding Principles:

The digital output of an ADC (ignoring quantization error) is:

Where:

V_in: Input signal voltage;

V_ref: Reference voltage;

N: Number of bits of the ADC;

Introducing Reference Voltage Noise

Assume:

Ideal reference voltage:

Actual reference voltage: V_ref + n, where n is a zero-mean, Gaussian-distributed disturbance of the reference voltage.

Thus:

The output encoding becomes:

Output Error Expression

Let the ideal output be:

Output error:

Using a first-order Taylor expansion (assuming n is small):

Substituting in:

Final Error Formula

Error Statistical Characteristics

If n is small, then:

This error will introduce SNR loss, and:

The larger the input voltage (closer to full scale), the more significant the error; the smaller the reference voltage (e.g., 1 V), the more sensitive the error; the more bits (24-bit vs 16-bit), the greater the impact.

Reference voltage noise modifies the actual size of the LSB,non-linearly injecting output errors, with the error being linearly related to n and proportional to V_ref, making itone of the main sources of error in high-precision ADCs.

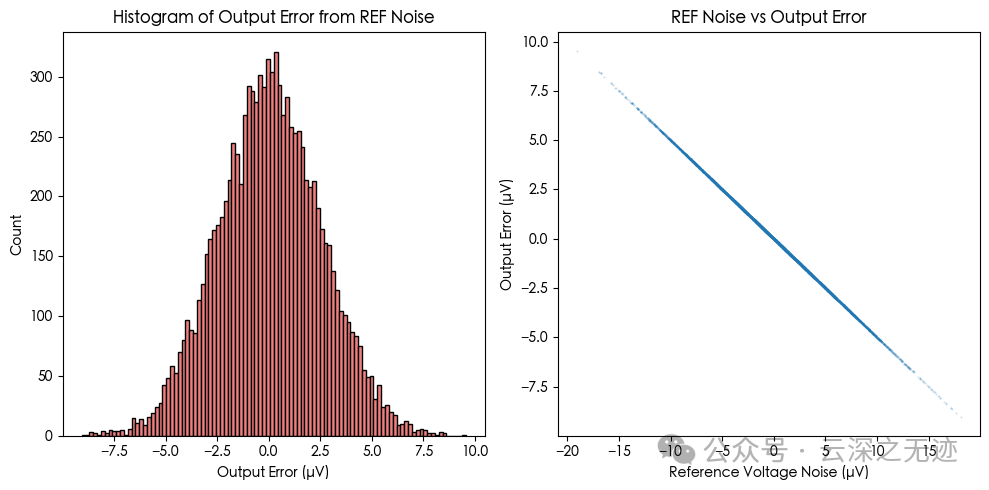
Simulations demonstrate how reference voltage noise affects the final ADC output through theLSB amplification mechanism:

Left Image: Output Error Distribution (in µV)

The distribution approximates a Gaussian shape; the mean is 0, but the standard deviation depends on the reference voltage noise; even a ±5 µV reference voltage jitter can lead to output errors close to ±1 LSB level.

Right Image: Reference Voltage Disturbance vs Output Error

The linear trend is evident;

Each point represents the output error corresponding to a single sample of <span>δV</span> (reference source noise);

The slope of the curve is the actual representation of our derived formula:

Next, we will simulate the impact of different noise levels on ENOB / SNR and the noise reduction model after adding an RC filter?

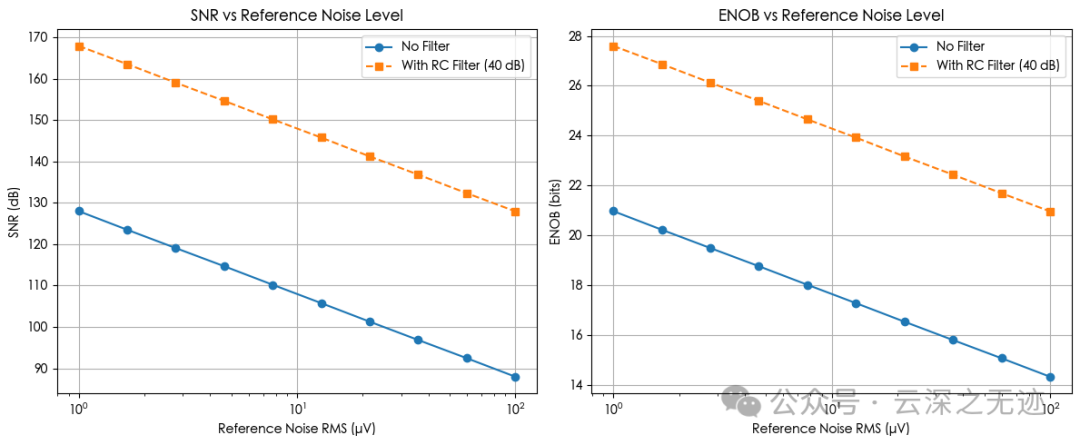
The figure shows:The greater the reference source noise → the lower the ADC SNR / ENOB, while adding an RC filter (assuming a 40 dB attenuation) can significantly suppress its impact.

Left Image: SNR vs Reference Noise (µV)

Without filtering, a 10 µV RMS reference noise can pull the SNR below 110 dB; after the filter is effective, the SNR can recover to nearly 140 dB at the same noise level.

Right Image: ENOB vs Reference Noise

You can see that without filtering, the ENOB drops from the theoretical 24-bit to 18-bit; but after RC filtering, the ENOB significantly rebounds, approaching the ideal ADC limit.

In high ENOB applications, the noise of the reference source is amplified by the LSB, making RC filtering crucial.