Click the blue text above “Hele Mathematics” to follow us and see more historical articles. Bookmark us to quickly read the latest articles.
Translation team member introduction: Lu
A physics enthusiast who loves programming and guitar. Welcome to add me. Are there any friends who like Unity? Let’s play together (๑˙ー˙๑)
English: plus.maths.org/content/elliptic-cryptography Translation: Lu Proofreading/Layout: Axiom Reprinted from: Meet Mathematics Note: If the numbers/formulas in the text appear too large, please click the upper right corner to “Refresh” to restore normal.
Elliptic curves are an important new area of mathematics that has been widely explored in recent decades. They show great potential as a tool for solving complex numerical problems and in applications in cryptography.
In 1994, Andrew Wiles and his former student Richard Taylor solved one of the most famous mathematical problems of the past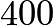 
years, Fermat’s Last Theorem, using elliptic curves. In recent decades, there has also been much research using elliptic curves as a replacement for the so-called RSA encryption to ensure the security of data transmission.
Public Key and Private KeyElliptic Curve Cryptography (ECC) is an algorithm for establishing public key encryption, similar to RSA cryptography. The basic idea behind it is a padlock. If I want to send you a secret message, I can ask you to send me an open padlock, but only you have the key. Then I put my letter in a box, lock it with the padlock, and send it to you. The benefit of this method is that the message can be sent through an insecure channel – even if someone intercepts the box, they do not have the key – and we do not all need the key to the box. You can even have many people send you secret messages this way without revealing any one key.
In public key cryptography, messages are encrypted using specific mathematical information that constitutes the public key. The encryption is performed using the public key, which is like closing the padlock. Decryption can only be done using a non-public mathematical private key, so even knowing the public key cannot be used for decryption.
In RSA cryptography, the public key involves a natural number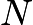 
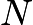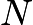, which is used by computers to encrypt messages. To decrypt the message, one needs to know the factors of . If is very large, then factoring it requires enormous computational power, making it practically impossible to crack. Only those who have the private key (i.e., the factors of 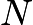) can easily decrypt the message.
Elliptic CurvesElliptic Curve Cryptography is based on the difficulty of solving elliptic curve discrete logarithm problems. At a simple level, these can be viewed as curves given by the following algebraic equation:
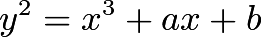
where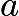 
and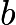 
are constants. Here are some examples. In each case, the graph shows all points with coordinates 
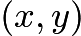, where 
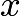and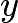 
satisfy the equation in the above form.
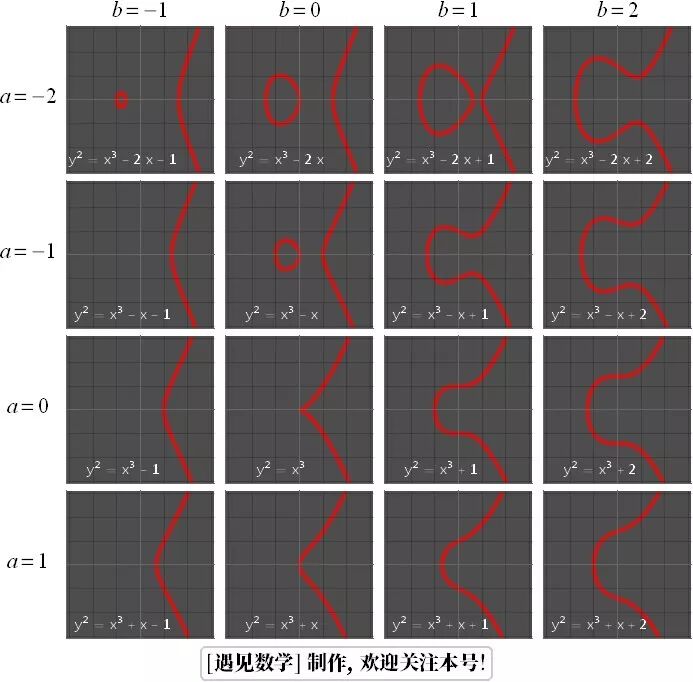
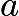Between 
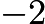and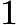 
the integer values corresponding to the elliptic curves, 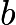between 
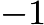and 
the integer values corresponding to the elliptic curves. Only the curve of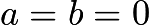 
does not satisfy the elliptic curve because it has a singular point. For precision, we need to restrict the constants and . Each curve equation given above can serve as an elliptic curve, and we need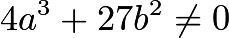 
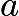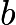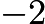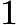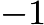. This ensures that the curve has no singular points. In layman’s terms, this means that the curve is smooth everywhere and does not contain any sharp points or self-intersections. In the examples above, the constants and were chosen as and , and between integers. But overall, they can also have other values. (In cryptography, 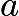and 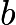must come from a special set of numbers called finite fields). In the link below, you can learn more about elliptic curves.plus.maths.org/content/very-old-question-very-latest-maths-fields-medal-lecture-manjul-bhargava
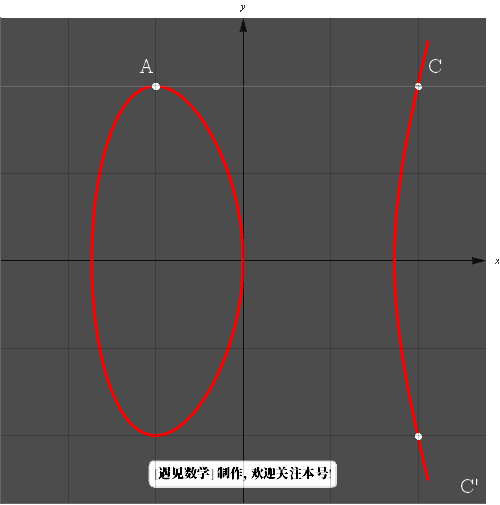
Defining Addition and Multiplication in Elliptic Curve CryptographyGiven an elliptic curve, we can define the addition of two points, as shown in the following example. First, let us consider the curve
The two points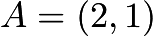 
and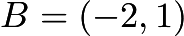 
are both on the curve. We now want to find the answer for 
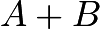, and we also want it to be on the elliptic curve. If we add them like vectors, we can 
. But unfortunately, that point is not on the curve. Therefore, we define addition on the elliptic curve through the following steps .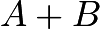
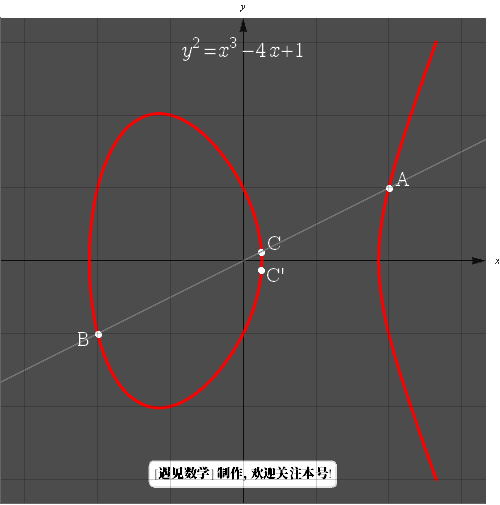
We connect the points 
and 
with a straight line. This line typically intersects the curve at another point 
. Then we reflect across the x-axis. We define this reflected image point 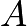as the sum of 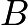and 
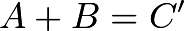. So
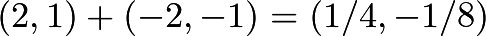
Let’s look at another example,
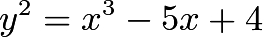
(as shown),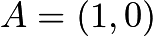 
and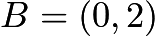 
, we have 
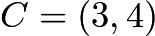and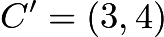 
. Therefore
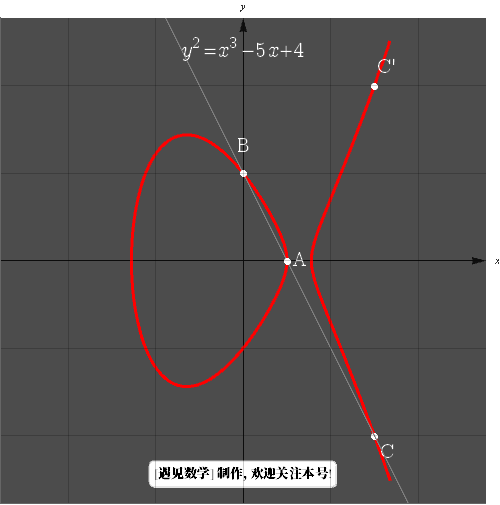
We also need to define the sum when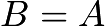 
to understand what we mean. In this case, we take the tangent value of the curve at the point 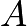, then find the intersection of this tangent line and the curve, and then find this image point. It may be easier to understand with the graph from another example. Here we consider the following elliptic curve
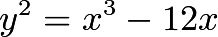
Consider the point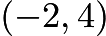 
we draw the tangent of the curve at the point (i.e., 
is the same point), the point 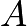intersects the curve at the point 
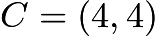reflecting across the x-axis gives 
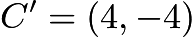. Therefore we say 
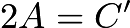, or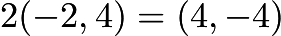 
.
Now we can define the meaning of A at any point on the curve and any natural number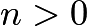 
.
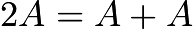
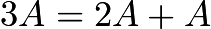
And so on for this accumulation process.
The only case where our definition for 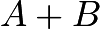does not work is when 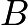is 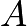at the reflection image point on the 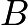, 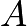on the same vertical axis. In this case, we are adding two points located on the same vertical line, and there is no third point that intersects with them. We can solve this problem by adding an extra point on the usual 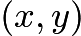plane, called infinity, represented by 
. To make addition applicable to our special case, we simply define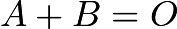 
. For any point, we also define 
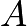, so with the new concept of addition, the point and the number in ordinary addition play the same role.The security of the elliptic curve encryption algorithm is based on the fact that given two points on the elliptic curve and 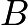, finding a number 
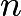such that 
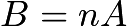(if it exists) requires enormous computational power, especially when 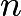is very large. Elliptic Curve Cryptography takes advantage of this fact: the points 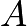and 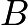can be used as public keys, and the number 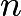can be used as a private key. Anyone can use the publicly available public key to encrypt messages (we will not go into detail about the encryption method here), but only individuals (or computers) with the private key (the number 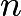) can decrypt them.
The NSA and Hacking DataElliptic Curve Cryptography has some advantages over RSA cryptography – RSA cryptography is based on the difficulty of factoring large integers – ECC requires shorter keys to produce the same or higher levels of security. Therefore, data can be encoded more efficiently (and thus faster) compared to RSA encryption. Currently, the digital currency Bitcoin uses elliptic curve encryption, and as more data becomes digitized, its use may become more widespread. However, it is worth noting that so far no one has proven that breaking elliptic curves is difficult – perhaps there is a new method that can solve this problem in a shorter time. In fact, many mathematicians and computer scientists are working in this field.
Government digital espionage agencies such as the NSA and GCHQ are also very interested in such encryption technologies. If there were a fast way to solve this problem, vast amounts of encrypted data could be accessed overnight – for example, Bitcoin exchanges would no longer be secure. Recently, there have also been reports that the NSA has implanted “backdoor” entries in some elliptic curve encryption algorithms, allowing the NSA to access data that others believe to be secure. Mathematics is the true core power in this new digital arms race. (End)
Tap “Looking” and share with friends!