1. Read Single-Ended S4P and Plot Graph
filename = 'data.s4p';backplane = sparameters(filename); % Read S4P file
data = backplane.Parameters; % Read S-parameter matrix data
freq = backplane.Frequencies; % Read frequency points
z0 = backplane.Impedance; % Read characteristic impedance
% IQS parameters
s11_iq = squeeze(data(1,1,:)); % S11
s12_iq = squeeze(data(1,2,:)); % S12
s13_iq = squeeze(data(1,3,:)); % S13
s14_iq = squeeze(data(1,4,:)); % S14
s21_iq = squeeze(data(2,1,:)); % S21
s22_iq = squeeze(data(2,2,:)); % S22
s23_iq = squeeze(data(2,3,:)); % S23
s24_iq = squeeze(data(2,4,:)); % S24
s31_iq = squeeze(data(3,1,:)); % S31
s32_iq = squeeze(data(3,2,:)); % S32
s33_iq = squeeze(data(3,3,:)); % S33
s34_iq = squeeze(data(3,4,:)); % S34
s41_iq = squeeze(data(4,1,:)); % S41
s42_iq = squeeze(data(4,2,:)); % S42
s43_iq = squeeze(data(4,3,:)); % S43
s44_iq = squeeze(data(4,4,:)); % S44
% Single-ended S-parameters
s11 = 20*log10(abs(s11_iq));
s12 = 20*log10(abs(s12_iq));
s13 = 20*log10(abs(s13_iq));
s14 = 20*log10(abs(s14_iq));
s21 = 20*log10(abs(s21_iq));
s22 = 20*log10(abs(s22_iq));
s23 = 20*log10(abs(s23_iq));
s24 = 20*log10(abs(s24_iq));
s31 = 20*log10(abs(s31_iq));
s32 = 20*log10(abs(s32_iq));
s33 = 20*log10(abs(s33_iq));
s34 = 20*log10(abs(s34_iq));
s41 = 20*log10(abs(s41_iq));
s42 = 20*log10(abs(s42_iq));
s43 = 20*log10(abs(s43_iq));
s44 = 20*log10(abs(s44_iq));
% Plot magnitude response curve
figure;
% subplot(1,1,1);
semilogx(freq/1e9, s11, 'b', 'LineWidth', 1.5); hold on;
semilogx(freq/1e9, s12, 'r', 'LineWidth', 1.5);
semilogx(freq/1e9, s13, 'g', 'LineWidth', 1.5);
semilogx(freq/1e9, s14, 'm', 'LineWidth', 1.5);
semilogx(freq/1e9, s21, 'b', 'LineWidth', 1.5);
semilogx(freq/1e9, s22, 'r', 'LineWidth', 1.5);
semilogx(freq/1e9, s23, 'g', 'LineWidth', 1.5);
semilogx(freq/1e9, s24, 'm', 'LineWidth', 1.5);
semilogx(freq/1e9, s31, 'b', 'LineWidth', 1.5);
semilogx(freq/1e9, s32, 'r', 'LineWidth', 1.5);
semilogx(freq/1e9, s33, 'g', 'LineWidth', 1.5);
semilogx(freq/1e9, s34, 'm', 'LineWidth', 1.5);
semilogx(freq/1e9, s41, 'b', 'LineWidth', 1.5);
semilogx(freq/1e9, s42, 'r', 'LineWidth', 1.5);
semilogx(freq/1e9, s43, 'g', 'LineWidth', 1.5);
semilogx(freq/1e9, s44, 'm', 'LineWidth', 1.5);
grid on;
xlabel('Frequency (GHz)');
ylabel('Magnitude (dB)');
title('SE S-Parameters Magnitude');
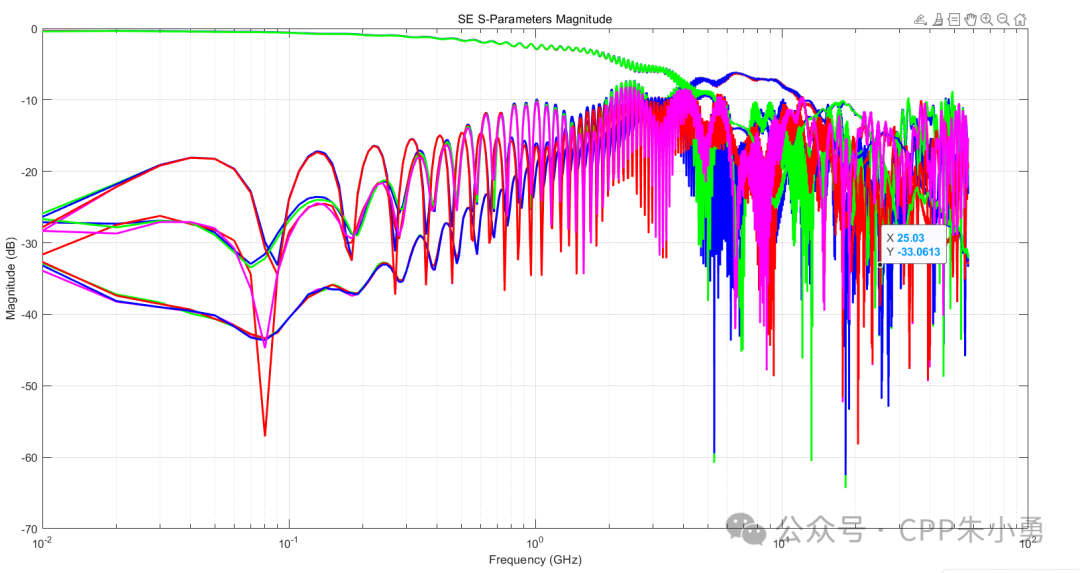2. Convert Single-Ended S4P to Balanced Ports (BAL-BAL) and Plot Graph
% SE to BAL-BAL
diffdata = s2sdd(data); % Use s2sdd function to extract differential S-parameters, 13,24
diffz0 = 2*z0;
diffsparams = sparameters(diffdata,freq,diffz0)% rfwrite(diffdata, freq, 'diffspara_1.s2p') % Write out new S2P file
% Extract components of differential S-parameters
sdd11 = squeeze(diffdata(1,1,:)); % SDD11
sdd21 = squeeze(diffdata(2,1,:)); % SDD21
sdd12 = squeeze(diffdata(1,2,:)); % SDD12
sdd22 = squeeze(diffdata(2,2,:)); % SDD22
% Convert to dB units
sdd11_dB = 20*log10(abs(sdd11));
sdd21_dB = 20*log10(abs(sdd21));
sdd12_dB = 20*log10(abs(sdd12));
sdd22_dB = 20*log10(abs(sdd22));
% Plot magnitude response curve
figure;
subplot(1,1,1);
semilogx(freq/1e9, sdd11_dB, 'b', 'LineWidth', 1.5); hold on;
semilogx(freq/1e9, sdd21_dB, 'r', 'LineWidth', 1.5);
semilogx(freq/1e9, sdd12_dB, 'g', 'LineWidth', 1.5);
semilogx(freq/1e9, sdd22_dB, 'm', 'LineWidth', 1.5);
grid on;
xlabel('Frequency (GHz)');
ylabel('Magnitude (dB)');
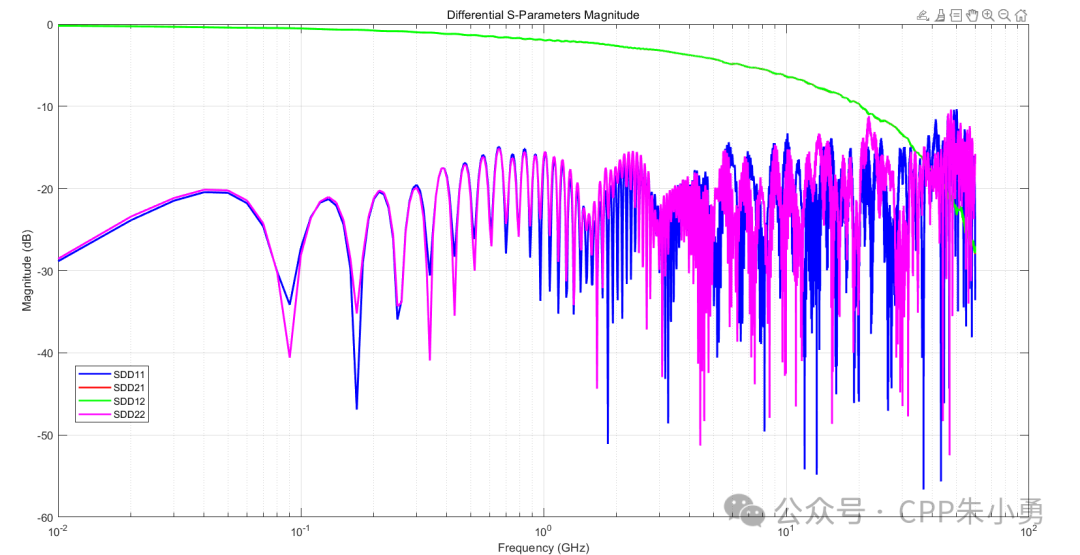
title('Differential S-Parameters Magnitude');
legend('SDD11', 'SDD21', 'SDD12', 'SDD22', 'Location', 'best');
In addition to SDD, other differential and common-mode S-parameter conversion functions can be referenced:
https://ww2.mathworks.cn/help/rf/ref/s2sdd.html
3. Convert Multi-Port Single-Ended S-Parameters to S4P and then to Balanced Ports (BAL-BAL) and Plot Graph
filename = 'data.s32p';backplane = sparameters(filename)
freq = backplane.Frequencies;
n2m = [1 17 2 18]; % Differential port setting
z0 = backplane.Impedance;
first4portdata = snp2smp(backplane.Parameters,z0,n2m,z0);
first4portsparams = sparameters(first4portdata,freq,z0)
diffdata = s2sdd(first4portdata) % Extract differential S-parameters for this pair
% rfwrite(diffdata, freq, 'diffspara.s2p') % Export new S-parameters
% Extract components of differential S-parameters
sdd11 = squeeze(diffdata(1,1,:)); % SDD11
sdd21 = squeeze(diffdata(2,1,:)); % SDD21
sdd12 = squeeze(diffdata(1,2,:)); % SDD12
sdd22 = squeeze(diffdata(2,2,:)); % SDD22
% Convert to dB units
sdd11_dB = 20*log10(abs(sdd11));
sdd21_dB = 20*log10(abs(sdd21));
sdd12_dB = 20*log10(abs(sdd12));
sdd22_dB = 20*log10(abs(sdd22));
% Plot magnitude response curve
figure;
subplot(1,1,1);
semilogx(freq/1e9, sdd11_dB, 'b', 'LineWidth', 1.5); hold on;
semilogx(freq/1e9, sdd21_dB, 'r', 'LineWidth', 1.5);
semilogx(freq/1e9, sdd12_dB, 'g', 'LineWidth', 1.5);
semilogx(freq/1e9, sdd22_dB, 'm', 'LineWidth', 1.5);
grid on;
xlabel('Frequency (GHz)');
ylabel('Magnitude (dB)');
title('Differential S-Parameters Magnitude');
legend('SDD11', 'SDD21', 'SDD12', 'SDD22', 'Location', 'best');
Reference:https://ww2.mathworks.cn/company/technical-articles/use-matlab-for-s-parameter-post-processing.html