
Source: PaperWeekly
This article is about 2800 words long and is recommended to be read in 6 minutes.
This article mainly introduces how a paper is born.
Nothing will work unless you do. ——Maya Angelou
This article mainly introduces how a paper is born. The basic information of the article is as follows:

Introduction: A Mixer matrix is added to the traditional LoRA to mix information from different subspaces. The design is very simple:
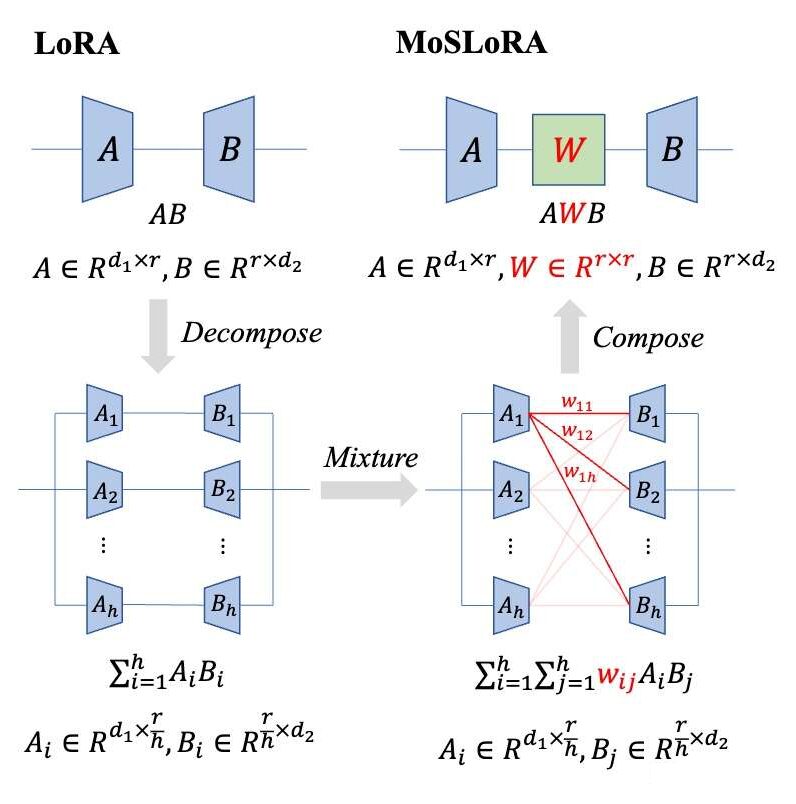
1. The Initial Idea
It is a coincidence that many articles have tried to combine LoRA and MoE, and they basically treat LoRA as the expert of MoE, then fit it into the MoE structure. Some have been introduced before, such as articles 1 2 3 4. These articles undoubtedly regard LoRA as the expert of MoE, which lacks motivation, affects the mergeability of LoRA, and slows down training.
While chatting with a colleague, he said he had never seen an article that fits MoE into LoRA. I was stunned at the time. Huh? Fitting MoE into LoRA means using MoE’s gate + multiple experts to do LoRA’s lora_A and lora_B?
The most intuitive design is:
In fact, coming up with this design is quite straightforward since both lora and MoE are mature and simple designs.
Let’s not talk about whether there is motivation; anyway, it’s a water article, and we can find something. However, this design is somewhat inappropriate; why?
The core issue lies in the Gate. MoE aims to train as many parameters as possible without increasing the computation too much, hence the design of multiple experts and the Gate Router mechanism. However, LoRA itself has a small number of parameters, and a large rank does not necessarily yield better results; piling on this parameter is indeed unnecessary.
Moreover, the advantage of LoRA is that it can merge back to the original weights, with 0 latency during inference. This Router Gate is coupled with the input x, so it cannot merge back. This introduces inference latency.
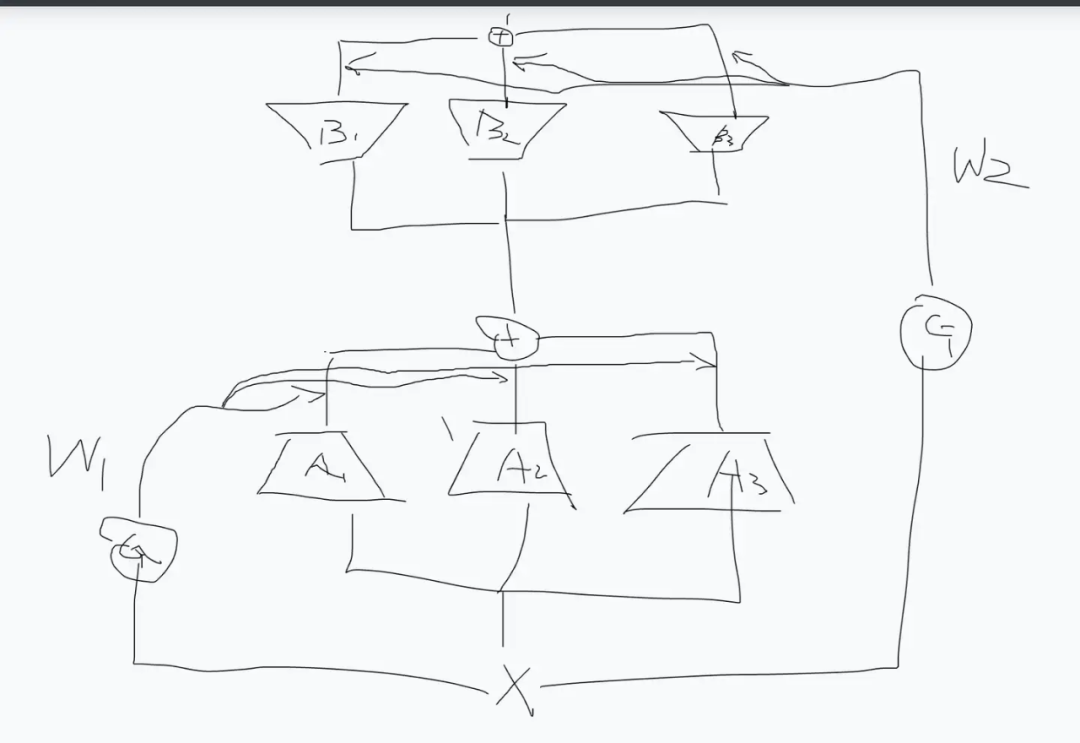
2. Remove the Gate, Go Directly
With the above analysis, the next step is naturally to remove the Gate. To ensure mergeability, all experts must be used; at this point, it becomes:
After this design, some concerns arise: although during inference, everyone can merge back into the original weights with 0 latency, during training, for example, the parameters trained are more than three times the previous ones (in today’s environment, this might get criticized by reviewers).
So to be fair, it cannot be set to r; each module still needs to be set to r/k, where the case in the above figure corresponds to r/3, so that the training parameters do not change while inference remains at 0 latency.
This is also the origin of the two-subspace-mixing method in the paper.
3. The Perspective of ‘Multi-Head Attention’
Since each expert is set to the size of r/k, this thing resembles multi-head attention, with dimension splitting + parallel operation + final merging. This makes me wonder what the relationship is with multi-head attention. Can the original LoRA be equivalently split?
Speaking of splitting, there are two quantities that can be split: one is rank and the other is the input dimension d. If we directly talk about multi-head, people might think of splitting d directly, rather than splitting rank. However, we can analyze both kinds of splitting:
i) Perspective of splitting d:
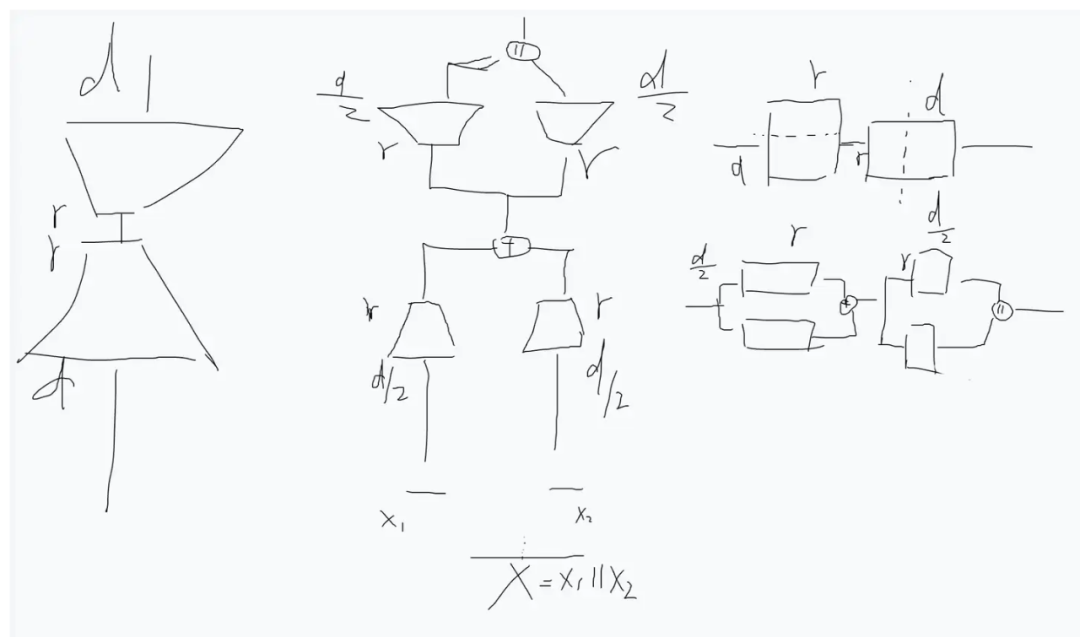
The figure shows the case of splitting d into 2 d/2. To make it easier to understand, I deliberately drew it from a matrix perspective. From the perspective of matrix operations, after splitting in the d dimension, it is equivalent to passing through two A’s, summing them, then passing through two B’s, and finally concatenating. These three perspectives are equivalent.
To be honest, there is really nothing to improve on this.
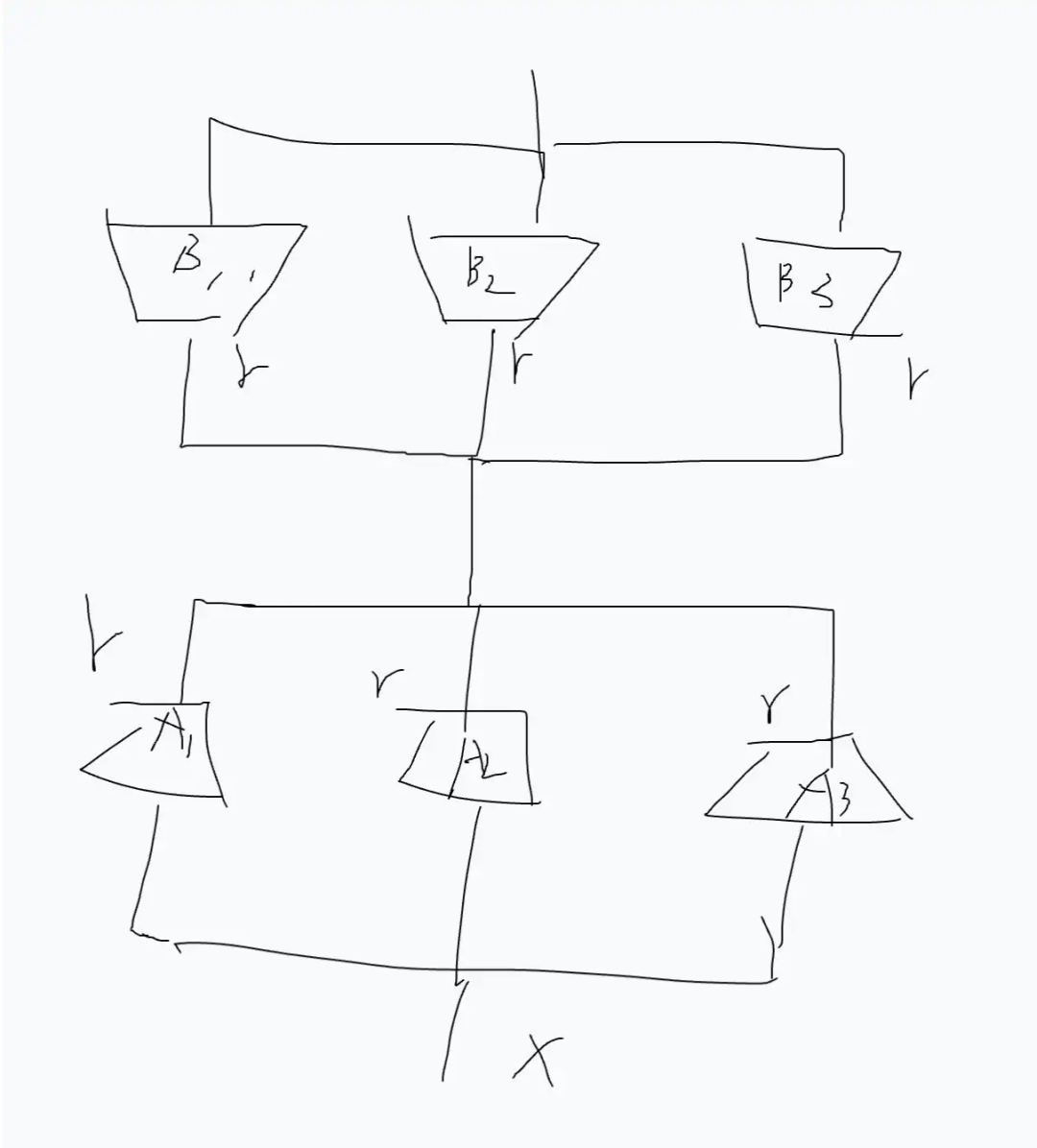
ii) Perspective of splitting r:
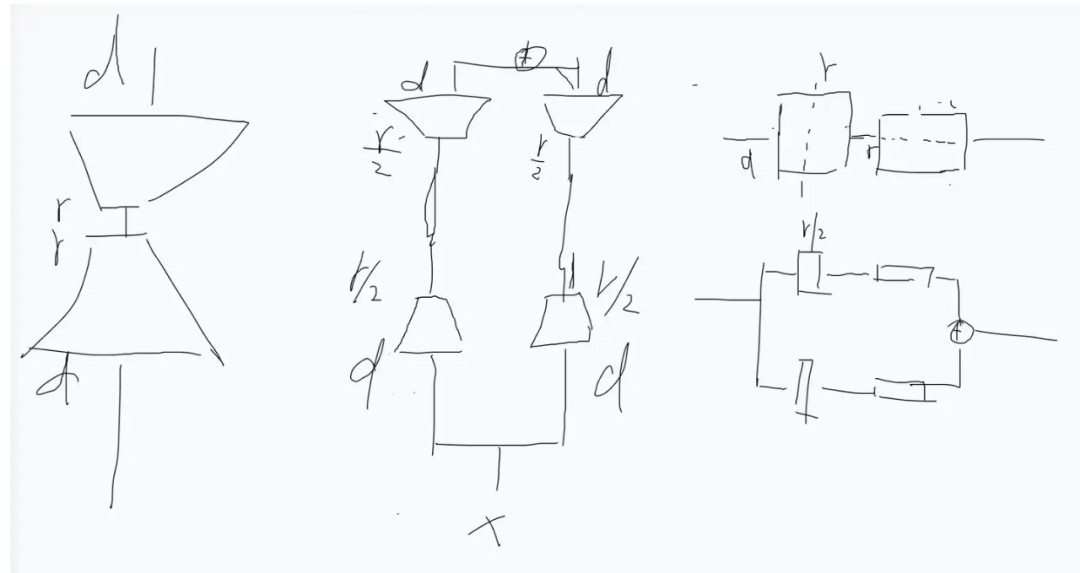
Similarly, rank can also be split. The above figure shows the process of splitting rank into two sub-blocks. It can be seen that it is equivalent to two branches, each with rank=r/2, and then summing. This is clearly more elegant than the previous method of splitting d.
From this perspective, a very simple improvement emerges:

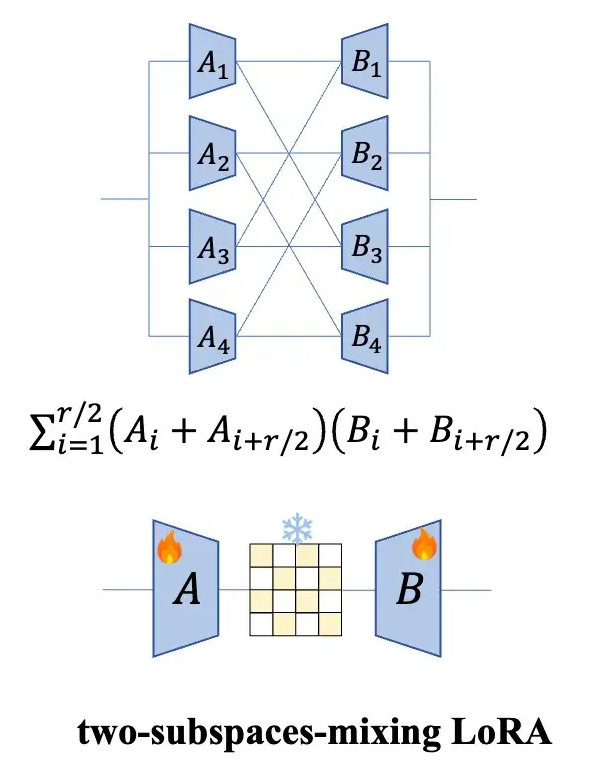
The idea is quite simple; it is to twist the parallel branches together. From a formulaic perspective, this changes from A1B1+A2B2 to (A1+A2)(B1+B2)=A1B1+A2B2+A1B2+A2B1.
This way, it adds two more terms. Let’s temporarily call this the twisted braid scheme.
4. Stage Results, But Not Enough
With the above analysis, we can start experimenting:
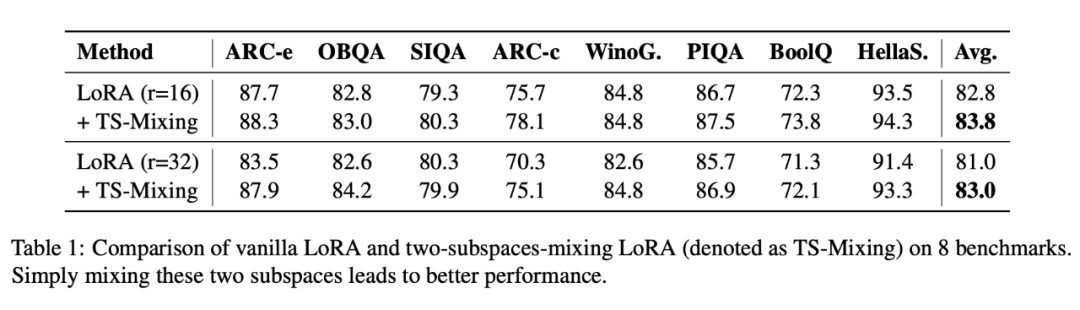
Fine-tuning LLaMA3 for commonsense reasoning, I found that there was still an improvement.
However, there’s another problem: the code efficiency is actually not high. Drawing a few parallel lines and then twisting a braid is simple, but the implementation depends on how to realize it. I initialized two experts sequentially to forward, so the computational efficiency is not high. Of course, one can also learn from MHA’s code, first doing the inference, then splitting the vector (equivalent to combining A1 and A2 into one linear layer during forward, obtaining the result, and then splitting the vector).
This inspired another thought, which is to say that this whole operation involves many linear layer splits and merges. Our previous analysis considered splitting and merging from the perspective of linear layers, without considering the splitting and merging of vectors. From the vector perspective, it is equivalent to:
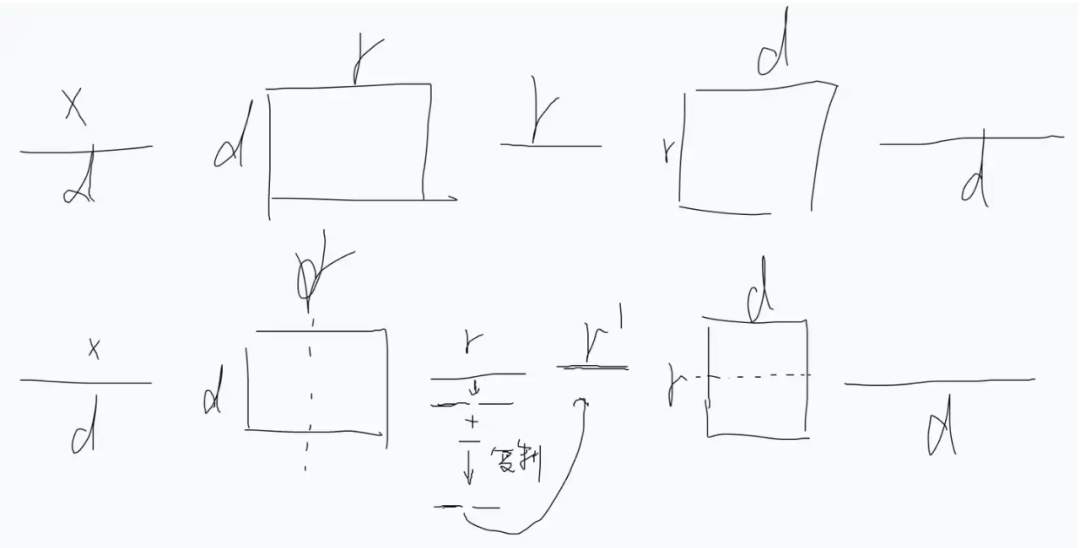
The previously mentioned twisted braid operation is equivalent to taking the r-dimensional vector in the middle, splitting it, summing it element-wise to half the length, then copying, and finally concatenating to obtain the final r’. From this perspective, this multi-expert twisted braid is essentially adding a set of combination punches on the r-dimensional vector.
5. Introduction of Mixing Matrices
Since it is adding a set of combination punches, what does this combination punch (r-dimensional vector, splitting, summing element-wise to half the length, then copying, and concatenating) look like from the matrix perspective?
Since this is the case, is it possible to imitate Tri Dao’s approach and introduce a bunch of butterfly matrix factors? However, after thinking about it, it still seems unnecessary because LoRA itself has a small computational load, and such splitting is not needed. Moreover, it might greatly increase latency (in addition, research found that butterfly matrix sequences are applied in the OFT series, which is BOFT).
Instead of going down the butterfly matrix sequence route, another intuitive idea is to upgrade this matrix to a learnable matrix. I refer to this matrix in the paper as the Mixer matrix, so:
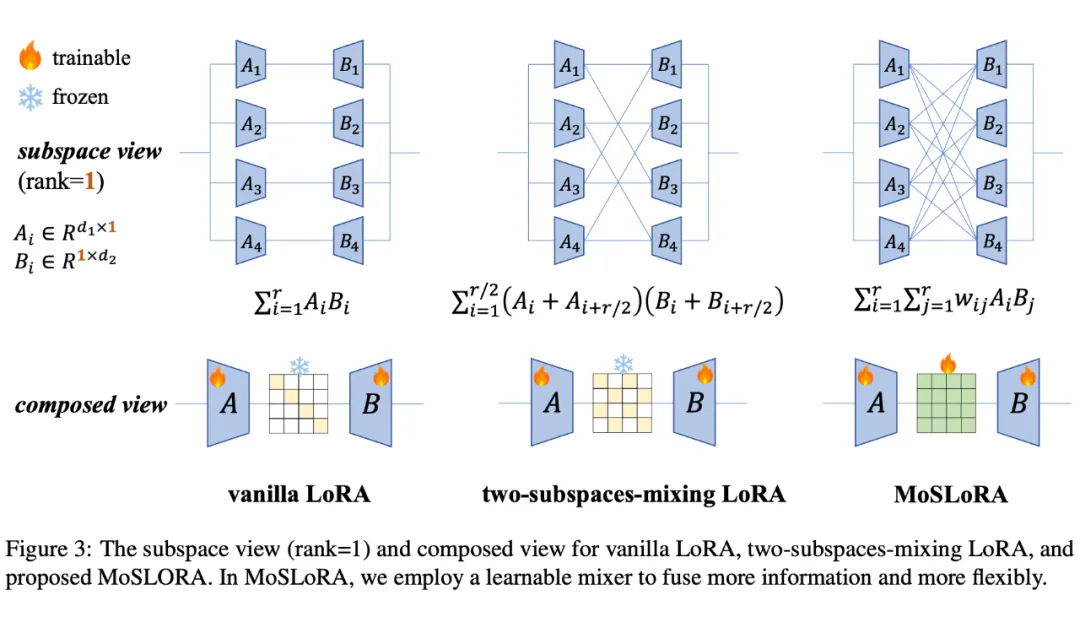
The original LoRA is equivalent to using a fixed identity matrix as the Mixer, the twisted braid scheme in the middle is equivalent to inserting a fixed butterfly factor matrix as the Mixer, and the paper upgrades it to a learnable Mixer, with all matrix elements being learnable, which is the proposed MoSLoRA method.
Note 1: This form is quite similar to AdaLoRA, but in AdaLoRA, the middle is a feature value from SVD decomposition, and both the front and back matrices have orthogonalization constraints added.
Note 2: While writing the paper, I found an excellent concurrent work on Arxiv, FLoRA: Low-Rank Core Space for N-dimension. Their paper approaches from the perspective of Tucker decomposition, and the idea is both clever and elegant. Those interested can also check out their article and interpretation.
6. Returning to the Perspective of MoE
Returning to the perspective of MoE, we go back to the diagram at the beginning of the paper:
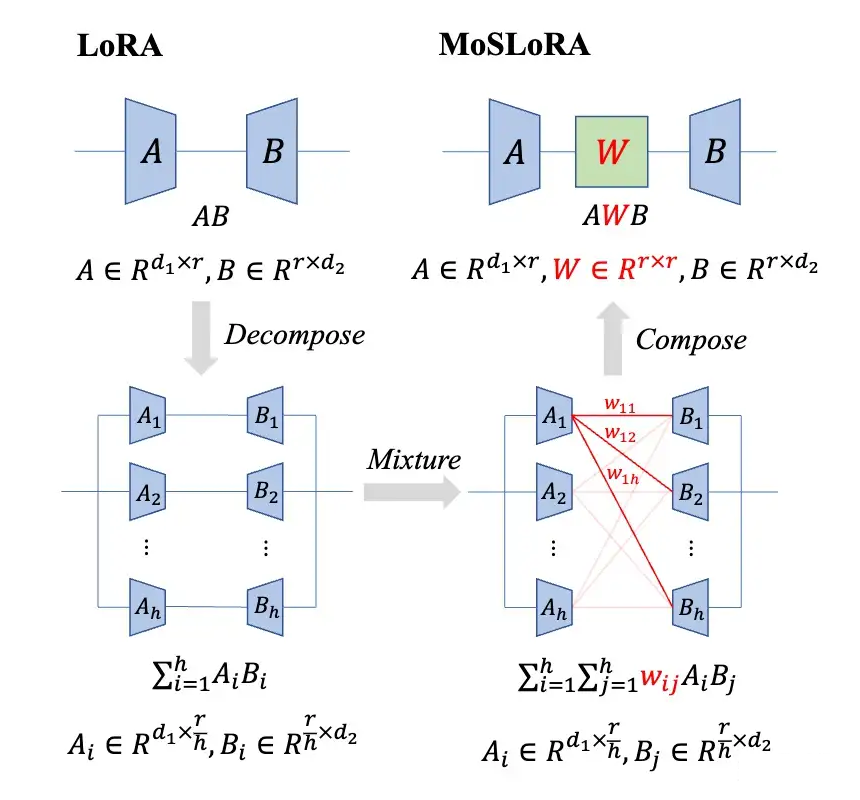
We can simply understand the Mixer as the weights generated by the MoE’s Gate, and this Gate has several characteristics:
-
This weight is independent of the input, ensuring mergeability.
-
This weight is dense, meaning all experts are utilized, rather than MoE’s top-k selection.
-
The original vanilla LoRA can be seen as this Mixer matrix being fixed to the identity matrix.
Seeing this, we can also understand another thing:
【Multiple parallel LoRA branches selecting top-k outputs and finally summing】 this conventional LoRA+MoE design is essentially equivalent to the Mixer having: i) each row being the same element ii) some rows being all zero iii) non-zero rows’ elements determined by the input iv) non-mergeable properties.
7. Postscript
By the time I write this, I have clarified the entire thought process. Of course, the paper cannot be written like this; it would be too lengthy and difficult to understand. Few people have the patience to read a blog post, let alone reviewers. However, the entire thought process has still yielded a lot of insights. Something that seems complex at first can become so simple after changing perspectives.
Supplementary Proof
Intuitively, if we insert a W in the middle, if we treat AW as A’, isn’t it the same as directly learning A’B?
Actually, it is not the same; even if the initialization is equivalent, it does not mean that the subsequent optimization paths are consistent. Just like reparameterization, although it seems equivalent, the learned results are different. From this perspective, the Mixer can also be seen as a form of reparameterization branch:
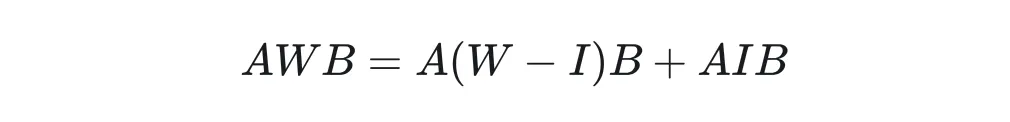
Where I is a fixed, non-learning matrix. This is equivalent to adding a parallel branch next to the original LoRA, consistent with reparameterization like RegVGG.
Of course, here is a simple proof that 【the subsequent optimization paths are not consistent】:
One can also look at the diagram directly:

Only when W is a fixed orthogonal matrix is it equivalent; otherwise, even if the initialization is the same, the optimization process will differ.
In MoSLoRA, W is learnable, and we analyzed the impact of initialization on the results.
About Us
Data派THU, as a public account for data science, backed by Tsinghua University’s Big Data Research Center, shares cutting-edge data science and big data technology innovation research dynamics, continuously disseminating knowledge in data science, striving to build a platform for gathering data talents, and creating the strongest group in China’s big data.

Sina Weibo: @Data派THU
WeChat Video Account: Data派THU
Today’s Headlines: Data派THU