As the parameter size of large models continues to grow, the cost of fine-tuning the entire model has gradually become unacceptable.
To address this, a research team from Peking University proposed a parameter-efficient fine-tuning method called PiSSA, which outperforms the widely used LoRA in fine-tuning effectiveness on mainstream datasets.
-
Paper: PiSSA: Principal Singular Values and Singular Vectors Adaptation of Large Language Models
-
Paper Link: https://arxiv.org/pdf/2404.02948.pdf
-
Code Link: https://github.com/GraphPKU/PiSSA
As shown in Figure 1, PiSSA (Figure 1c) has the same model architecture as LoRA [1] (Figure 1b), but the initialization method for the Adapter is different. LoRA initializes A with Gaussian noise and B with 0. In contrast, PiSSA uses the principal singular values and singular vectors to initialize A and B.
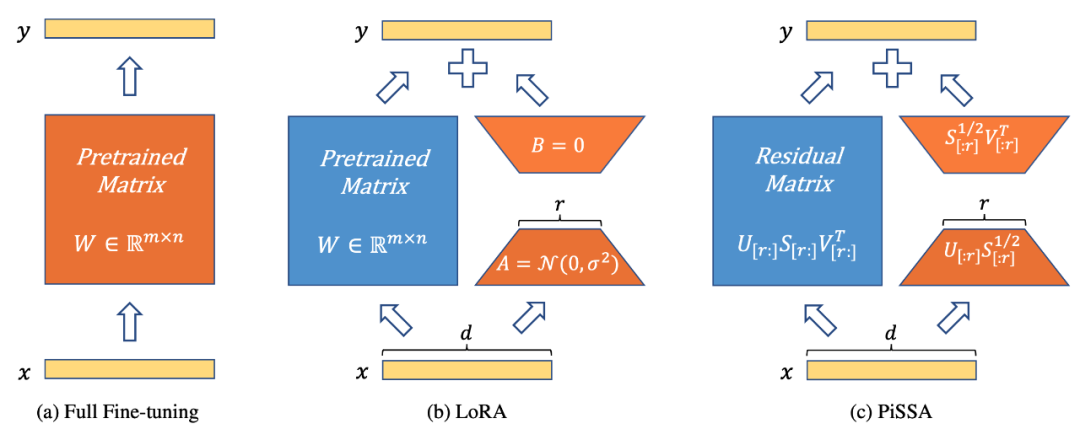
Figure 1) From left to right: full parameter fine-tuning, LoRA, and PiSSA. Blue represents frozen parameters, orange represents trainable parameters and their initialization methods. Compared to full parameter fine-tuning, both LoRA and PiSSA significantly reduce the amount of trainable parameters. For the same input, the initial outputs of these three methods are identical. However, PiSSA freezes the secondary components of the model and fine-tunes the main components (the first r singular values and singular vectors); whereas LoRA can be viewed as freezing the main parts of the model and fine-tuning the noise part.
Comparison of Fine-Tuning Effects of PiSSA and LoRA on Different Tasks
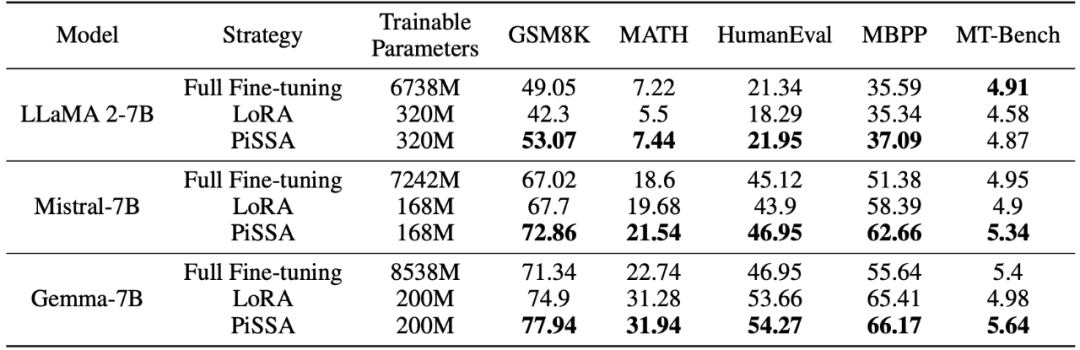
The research team used llama 2-7B, Mistral-7B, and Gemma-7B as base models to enhance their mathematical, coding, and conversational abilities through fine-tuning. This includes training on MetaMathQA and validating the model’s mathematical abilities on GSM8K and MATH datasets; training on CodeFeedBack and validating the model’s coding abilities on HumanEval and MBPP datasets; training on WizardLM-Evol-Instruct and validating the model’s conversational abilities on MT-Bench. From the experimental results in the table below, it can be seen that with the same scale of trainable parameters, the fine-tuning effect of PiSSA significantly surpasses that of LoRA, even exceeding that of full parameter fine-tuning.
Comparison of Fine-Tuning Effects of PiSSA and LoRA with Different Trainable Parameter Amounts
The research team conducted ablation experiments on the relationship between the amount of trainable parameters and the effects on mathematical tasks. From Figure 2.1, it is observed that in the early training phase, the training loss of PiSSA drops particularly quickly, while LoRA shows a phase where it does not decrease, and even slightly increases. Furthermore, the training loss of PiSSA remains lower than that of LoRA throughout the process, indicating a better fit to the training set. From Figures 2.2, 2.3, and 2.4, it is evident that under each setting, the loss of PiSSA is consistently lower than that of LoRA, and the accuracy is always higher than that of LoRA, demonstrating that PiSSA can achieve results comparable to full parameter fine-tuning with fewer trainable parameters.
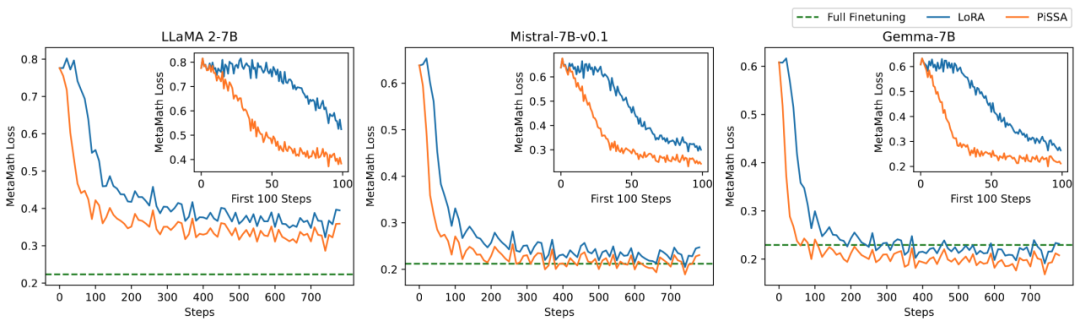
Figure 2.1) Loss during the training process of PiSSA and LoRA with rank 1. The upper right corner of each figure shows an enlarged curve of the first 100 iterations. PiSSA is represented by the orange line, LoRA by the blue line, and full parameter fine-tuning is shown with the green line as a reference. The phenomena are consistent with ranks [2,4,8,16,32,64,128], as detailed in the article appendix.
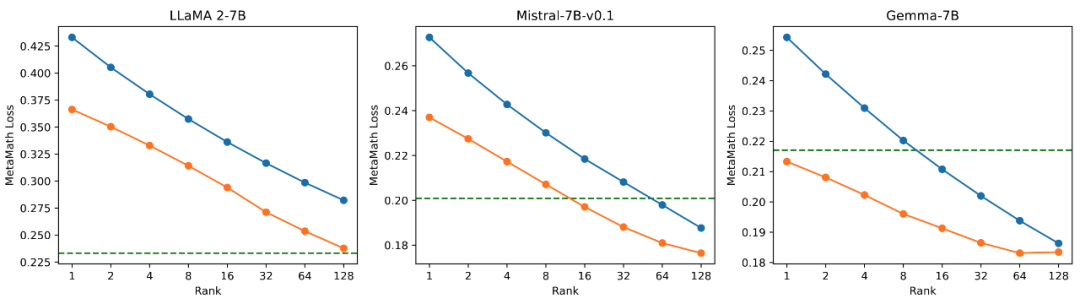
Figure 2.2) Final training loss of PiSSA and LoRA using ranks [1,2,4,8,16,32,64,128].
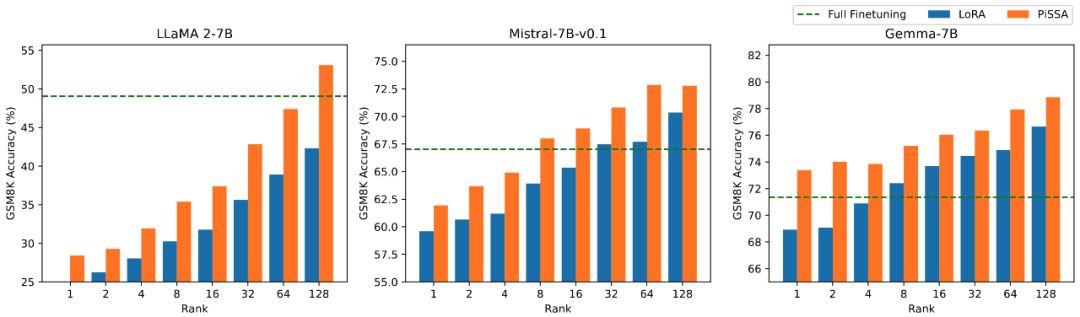
Figure 2.3) Accuracy of models fine-tuned with PiSSA and LoRA on GSM8K using ranks [1,2,4,8,16,32,64,128].
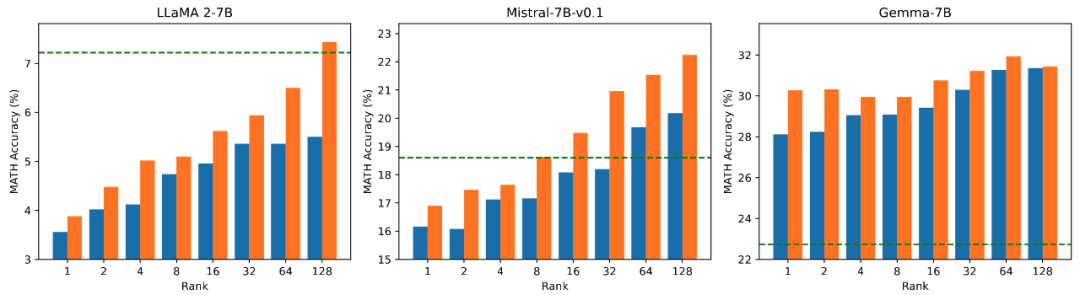
Figure 2.4) Accuracy of models fine-tuned with PiSSA and LoRA on MATH using ranks [1,2,4,8,16,32,64,128].
Detailed Explanation of the PiSSA Method
Inspired by Intrinsic SAID [2] that “the parameters of pre-trained large models exhibit low rank,” PiSSA performs singular value decomposition on the parameter matrix of the pre-trained model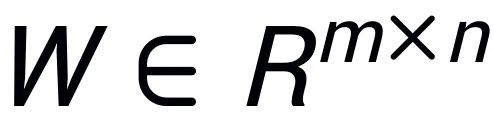
, where the first r singular values and singular vectors are used to initialize the two matrices of the adapter (adapter)
and 
, 
; the remaining singular values and singular vectors are used to construct the residual matrix
, ensuring that
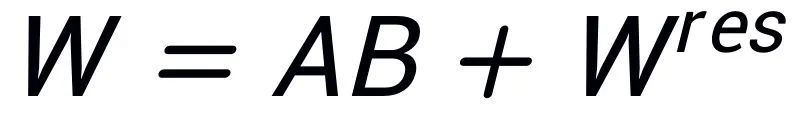. Therefore, the parameters in the adapter contain the core parameters of the model, while the parameters in the residual matrix are the corrective parameters. By fine-tuning the core adapters A and B with a smaller number of parameters while freezing the larger number of parameters in the residual matrix
, it achieves the effect of approximating full parameter fine-tuning with very few parameters.
Although PiSSA is also inspired by Intrinsic SAID [1], the principles behind PiSSA and LoRA are fundamentally different.
LoRA posits that the change in the matrix before and after fine-tuning the large model, △W, has a very low intrinsic rank r, thus simulating the model’s change △W through
and 
multiplied together to obtain the low-rank matrix. In the initial phase, LoRA initializes A with Gaussian noise and B with 0, thus
, ensuring that the model’s initial capability remains unchanged, and fine-tuning A and B achieves updates to W. In contrast, PiSSA does not concern itself with △W, but rather assumes that W has a very low intrinsic rank r. Therefore, it directly performs singular value decomposition on W, breaking it down into principal components A, B, and residual terms
, ensuring that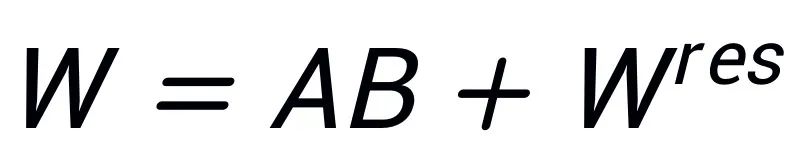
. Assuming the singular value decomposition of W is
, A and B are initialized using the largest r singular values and singular vectors after SVD decomposition:
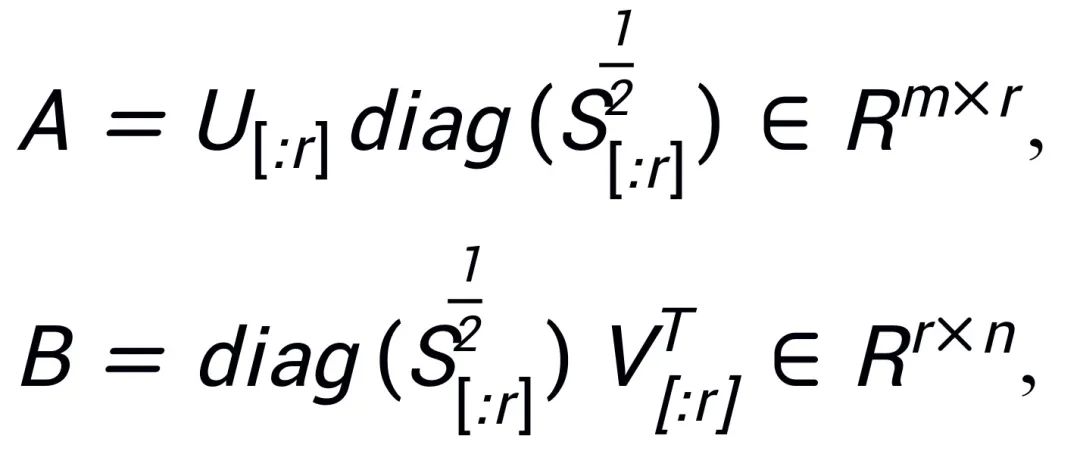
The residual matrix is initialized using the remaining singular values and singular vectors:
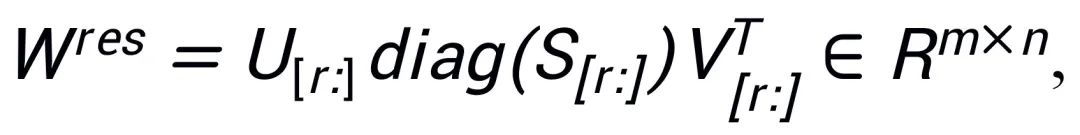
PiSSA directly fine-tunes the low-rank principal components A and B of W, freezing the secondary correction terms. Compared to LoRA, which initializes adapter parameters with Gaussian noise and 0 while freezing core model parameters, PiSSA converges faster and performs better.
The pronunciation of PiSSA is similar to “pizza”—if we compare the entire large model to a whole pizza, PiSSA cuts off one corner, which is the most filling part (the principal singular values and singular vectors), and re-bakes (fine-tunes on downstream tasks) it to the desired flavor.
Since PiSSA adopts the same architecture as LoRA, it can serve as an optional initialization method for LoRA, easily modified and called in the peft package (as shown in the following code). The same architecture also allows PiSSA to inherit most of LoRA’s advantages, such as: using 4-bit quantization for the residual model [3] to reduce training overhead; after fine-tuning, the adapter can be merged into the residual model without changing the model architecture during inference; there is no need to share the full model parameters, only the much smaller PiSSA module needs to be shared, allowing users to load the PiSSA module directly for automatic singular value decomposition and assignment; a model can simultaneously use multiple PiSSA modules, etc. Some improvements to the LoRA method can also be combined with PiSSA: for example, not fixing the rank at each layer and finding the optimal rank through learning [4]; using PiSSA-guided updates [5] to break through rank limitations, etc.
# Adding a PiSSA initialization option after LoRA's initialization method in the peft package:
if use_lora:
nn.init.normal_(self.lora_A.weight, std=1 /self.r)
nn.init.zeros_(self.lora_B.weight)
elif use_pissa:
Ur, Sr, Vr = svd_lowrank (self.base_layer.weight, self.r, niter=4)
# Note: Since the dimensions of self.base_layer.weight are (out_channel,in_channel), the order of AB is reversed compared to the diagram.
self.lora_A.weight = torch.diag (torch.sqrt (Sr)) @ Vh.t ()
self.lora_B.weight = Ur @ torch.diag (torch.sqrt (Sr))
self.base_layer.weight = self.base_layer.weight - self.lora_B.weight @ self.lora_A.weightComparison of Fine-Tuning Effects of High, Medium, and Low Singular Values
To verify the impact of using different sizes of singular values and singular vectors to initialize the adapter on the model, researchers used high, medium, and low singular values to initialize the adapters of LLaMA 2-7B, Mistral-7B-v0.1, and Gemma-7B, and then fine-tuned on the MetaMathQA dataset. The experimental results are displayed in Figure 3. From the figure, it can be seen that the method using principal singular values for initialization achieves the lowest training loss and higher accuracy on the GSM8K and MATH validation sets. This phenomenon confirms the effectiveness of fine-tuning the principal singular values and singular vectors.
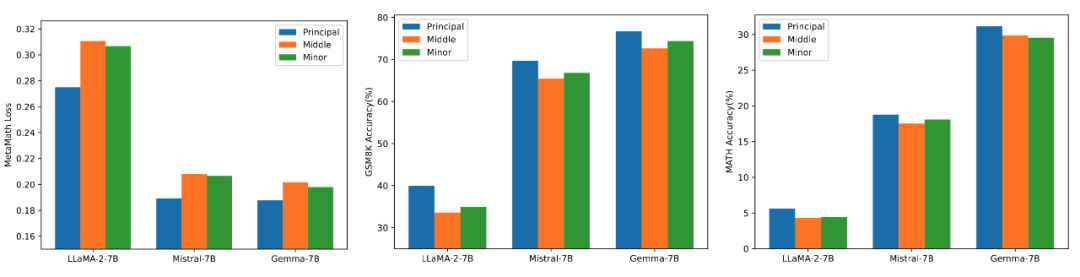
Figure 3) From left to right: training loss, accuracy on GSM8K, and accuracy on MATH. Blue represents the maximum singular value, orange represents the medium singular value, and green represents the minimum singular value.
Fast Singular Value Decomposition
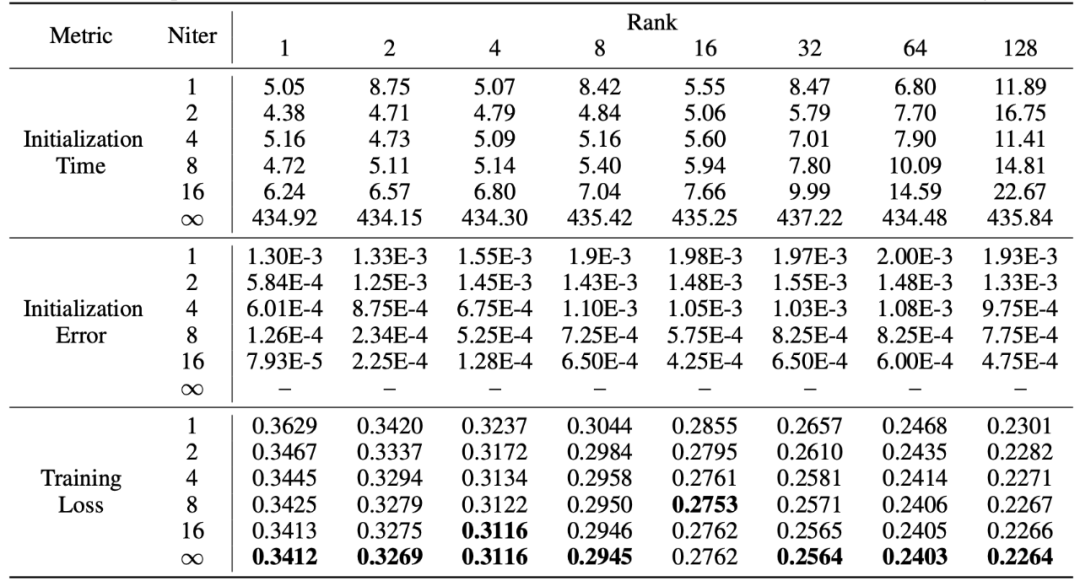
PiSSA inherits the advantages of LoRA, being convenient to use and outperforming LoRA. The cost is that during the initialization phase, the model requires singular value decomposition. Although it only needs to be decomposed once at initialization, it may still take several minutes or even tens of minutes. Therefore, researchers used a fast singular value decomposition [6] method to replace the standard SVD decomposition. The experimental results in the table show that it takes only a few seconds to approximate the training set fitting effect of the standard SVD decomposition. Here, Niter indicates the number of iterations; the larger Niter, the longer the time but the smaller the error. Niter = ∞ indicates standard SVD. The average error in the table represents the average L_1 distance between A and B obtained from fast singular value decomposition and standard SVD.
Summary and Outlook
This work performs singular value decomposition on the weights of pre-trained models, using the most important parameters to initialize an adapter called PiSSA, and fine-tuning this adapter to approximate the effect of fine-tuning the complete model. Experiments show that PiSSA converges faster and achieves better final results than LoRA, with the only cost being a few seconds of SVD initialization process.
So, would you be willing to spend a few extra seconds for better training results by changing LoRA’s initialization to PiSSA with one click?
References
[1] LoRA: Low-Rank Adaptation of Large Language Models
[2] Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning
[3] QLoRA: Efficient Finetuning of Quantized LLMs
[4] AdaLoRA: Adaptive Budget Allocation for Parameter-Efficient Fine-Tuning
[5] Delta-LoRA: Fine-Tuning High-Rank Parameters with the Delta of Low-Rank Matrices
[6] Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions
© THE END
For reprints, please contact this public account for authorization
Submissions or inquiries: [email protected]