
MLNLP community is a well-known machine learning and natural language processing community both domestically and internationally, covering NLP graduate students, university professors, and corporate researchers.The vision of the community is to promote communication and progress between the academic and industrial sectors of natural language processing and machine learning, especially for beginners.
Paper Title: Soft Reasoning: Navigating Solution Spaces in Large Language Models through Controlled Embedding Exploration
Paper Link: https://arxiv.org/pdf/2505.24688
Code Link: https://github.com/alickzhu/Soft-Reasoning/
This paper has been accepted as a spotlight at ICML 2025, and the author, Zhu Qinglin, is a PhD student at King’s College London.
Research Background and Core Issues
Large Language Models (LLMs) perform excellently in various reasoning tasks but still face significant challenges when dealing with complex reasoning tasks (e.g., mathematical reasoning). Existing methods typically enhance reasoning capabilities by increasing sampling diversity or introducing heuristic strategies, but these methods often struggle to effectively balance “exploration” and “exploitation,” leading to low reasoning efficiency or insufficient accuracy.
This paper starts from a key phenomenon: the reasoning process is greatly influenced by the first token. We believe that the traditional method of relying solely on selecting tokens from a candidate word list fails to fully exploit the expressive diversity contained in the large model’s vast parameters. Therefore, we use continuous vectors with large norms to replace the embedding of the first discrete token. Since the subsequent generation process uses greedy search, each different continuous vector corresponds to a unique generated text and validation result, thus establishing an optimizable one-to-one correspondence between continuous vectors, generated text, and validation results. We further use the validation results as reward signals to directly optimize the continuous vector corresponding to the first token, generating text with higher rewards, thereby significantly improving reasoning performance.
The core advantage of this method is that, compared to traditional temperature-based sampling strategies, we can efficiently resample those answers that have low generation probabilities but high validation rewards. In traditional temperature sampling, such answers often require numerous random attempts to capture; however, in this method, once such solutions are located, they will be frequently sampled and continuously contribute during the optimization process, significantly improving optimization efficiency and reasoning quality.
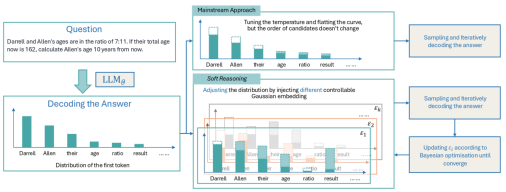
Comparison of traditional temperature scaling vs embedding perturbation probability distributions
Specifically, traditional methods (such as temperature scaling and multi-path sampling) have two major flaws:
Blindness: Temperature scaling uniformly increases the weights of low-probability tokens, often introducing noise rather than effective exploration.
Inefficiency: Prompt-based searches (such as Tree of Thoughts) rely on language descriptions and do not directly optimize internal hidden layer representations, often leading to inefficient searches.
To address these challenges, we propose Soft Reasoning, a search framework based on word embeddings that guides reasoning generation by optimizing the embedding of the first generated token. This method is characterized by:
1. Embedding Perturbation: By adding controllable Gaussian noise to the embedding of the first generated token, we adjust the probability distribution of the generated tokens, making the generation process more flexible and more controllable than temperature adjustment, allowing for the direct generation of low-probability answers.
2. Bayesian Optimization: Applying Bayesian optimization to the controlled perturbation of embeddings, guided by verifier feedback, to optimize the selection of reasoning paths through Expected Improvement.
3. No Additional Verifier Required: This method does not require an external verifier; it can improve generation quality through intrinsic optimization, with the advantages of low computational overhead and no need for specific model parameters.
Unlike traditional temperature adjustment or heuristic methods, our approach precisely controls the direction of the reasoning process by optimizing the embedding of the first token, avoiding the noise and inefficiency issues caused by blindly increasing diversity.
Method
The Soft Reasoning framework consists of three main modules, including Embedding Perturbation, Verifier-Guided Objective Function, and Bayesian Optimization Process in the Embedding Space
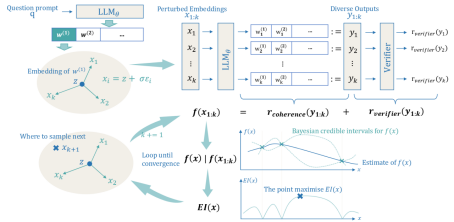
Soft Reasoning Algorithm Flowchart
1. Embedding Perturbation
Core Idea: Perturb the embedding of the first generated token with Gaussian noise to generate diverse candidate solutions.
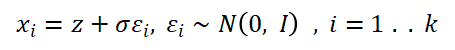
Key Steps:
a. Initial Embedding: z is the original word embedding of the first token generated by the model
b. Controllable Perturbation: Control the noise intensity with standard deviation σ to generate k candidate embeddings {x_i}; here we set the default standard deviation to 1, which is significantly higher than the token standard deviation of most language models. This means that the overall noise intensity will greatly change the norm of the first token, thus significantly affecting the results.
c. Deterministic Generation: For each x_i, use greedy decoding to generate the complete sequence y_i, ensuring a one-to-one mapping between x_i and y_i.
The advantage of this strategy is that it avoids global probability distribution flattening (compared to temperature scaling) and directs adjustments to low-probability tokens.
2. Verifier-Guided Objective Function
Objective Function Design:
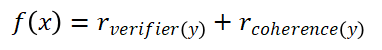
Component Analysis:
1. Verifier Score r_verifier(y): Use the same model as a verifier to determine whether the generated answer y is consistent with the verifier’s answer y_v.
2. Coherence Score r_coherence(y): Calculate the sum of the log probabilities of the token pairs in the generated sequence to assess semantic fluency.
The starting point of this strategy is that during the perturbation generation process in the previous step, there may be an excessive focus on decoding low-probability tokens. To balance this tendency’s disruption to semantic coherence, we introduce different scoring metrics to retain more coherent decoding results in high-probability regions. Additionally, considering both estimated costs (r_verifier(y)) and actual costs (r_coherence(y)), aligns better with heuristic search intuition.
3. Bayesian Optimization Process in the Embedding Space
In this work, we treat the objective function as a black box model, without explicitly analyzing or modeling its internal parameters, viewing it merely as a function that can output scores, but whose specific expression is unknown. In question-answering tasks (QA), we treat each question as an independent black box, whose output verification score changes with the different vectors we insert. With our constructed one-to-one mapping mechanism, we can search for a set of optimal vectors in the search space corresponding to each question, maximizing the scores obtained in the verifier.
To achieve this goal, we employ the Bayesian Optimization algorithm. The main reason for choosing this method is that Bayesian optimization is an efficient algorithm specifically designed for finding extrema of black box functions, suitable for scenarios where the form of the objective function is unknown and gradients are unavailable. This method models the function values of an existing set of sampled points, using Gaussian process regression to predict the probability distribution of function values at any input. Subsequently, based on this distribution, we construct an acquisition function to measure the exploration value of each candidate point. By maximizing the acquisition function, we determine the next optimal sampling point, and after multiple iterations, we ultimately return the optimal value obtained from all sampled points as an approximate solution to the maximum of the objective function.
Specific operations are as follows:
a. We treat the objective function f(·) as a black box and use a Gaussian process (GP) as its surrogate model, initializing the observation batch {(x_i,f(x_i))}_i=1^k
b. In the t-th iteration, based on the current surrogate model, we use Expected Improvement (EI) as the acquisition function to select the next query point:
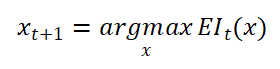
The EI function can balance “exploration” (uncertain regions) and “exploitation” (high-score regions), automatically guiding the search process closer to potential optimal areas.
c. Evaluate the selected sampling points to obtain their true objective function values and add that point to the observation set. The surrogate model is then updated to more accurately reflect the current function trend.
d. Repeat steps 2 and 3 until the termination conditions are met. Termination conditions include the current round’s EI value falling below a preset threshold (indicating model convergence) or reaching the maximum number of iterations.
e. In the specific operational process, we choose a random projection strategy to reduce high-dimensional embeddings to low-dimensional ones to alleviate the high-dimensional optimization problem.
Compared to traditional methods of adjusting temperature for sampling, in Bayesian optimization-based sampling, the results of each round of sampling draw on the results of previous rounds, allowing for targeted adjustments to related parameters, making the entire sampling process more controllable and efficient.
Experimental Validation and Key Results
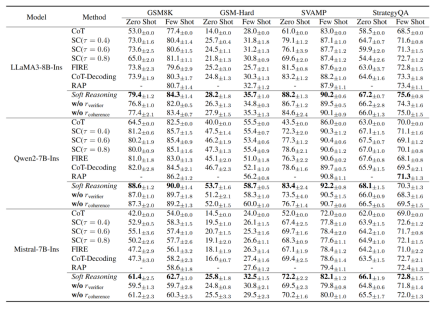
(1) Comprehensive Performance Improvement
(2) Mechanism Effectiveness Analysis: In analyzing the relevant experimental results, we can observe the following phenomena:
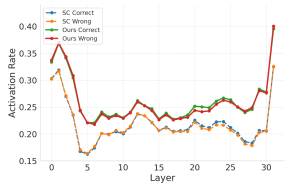
MLP activation rates of each layer of the Transformer (sampling 200 times, taking the first five tokens of the generated answers)
1. Neuron Activation Diversity: Soft Reasoning increases the activation rate of the Transformer MLP layer by 3-4%, triggering more key reasoning paths;
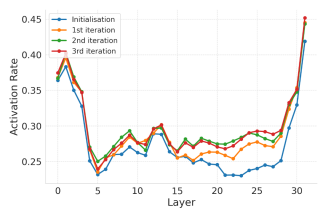
Moreover, the activation rate of key neurons gradually increases with the number of optimization rounds.
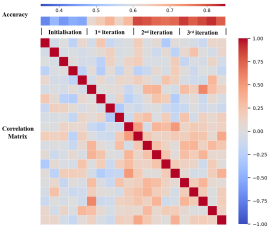
2. During the Bayesian optimization process, as the number of iterations increases, the controllable embedding correlation continues to increase, and performance improves.
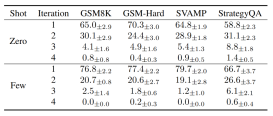
Proportion of test samples terminated in the n-th iteration
3. Convergence Efficiency: Most tasks converge in the first two rounds.
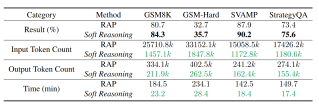
Comparison of Soft Reasoning and RAP in terms of performance and token consumption
4. Reasoning Cost: Compared to the baseline RAP based on MCTS search trees, it improves reasoning performance while significantly reducing reasoning costs.
Technical Group Invitation

△ Long press to add the assistant
Scan the QR code to add the assistant on WeChat
Please note:Name – School/Company – Research Direction (e.g., Xiao Zhang – Harbin Institute of Technology – Dialogue System)to apply for joiningNatural Language Processing/Pytorch and other technical groups
About Us
MLNLP community is a grassroots academic community jointly established by scholars in machine learning and natural language processing from both domestic and international backgrounds. It has developed into a well-known community for machine learning and natural language processing, aiming to promote progress between the academic and industrial sectors of machine learning and natural language processing, as well as among enthusiasts.The community provides an open communication platform for related practitioners’ further education, employment, and research. Everyone is welcome to follow and join us.