PID Control Principles, Case Analysis, and MATLAB Implementation

1. Introduction to PID Control

The PID (Proportional-Integral-Derivative) controller is the most classic feedback control algorithm in industrial control. It generates the control quantity through a linear combination of the proportional (Proportional), integral (Integral), and derivative (Derivative) parts of the error signal, achieving precise control of the system.

Mathematical Model of PID Controller:

2. Case Analysis: DC Motor Speed Control

Problem Description

Control the speed of a DC motor to quickly track the target speed (1000 RPM) and suppress load disturbances.

System Model

The simplified transfer function of the motor is:

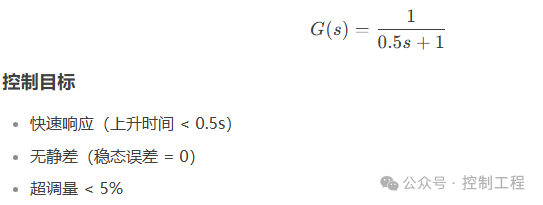
3. MATLAB Simulation Implementation

Step 1: Establish System Model

s = tf(‘s’);

sys = 1 / (0.5*s + 1); % Motor transfer function

Step 2: Design PID Controller

Preliminary parameter determination by trial and error:

Kp = 1.2;

Ki = 0.5;

Kd = 0.1;

C = pid(Kp, Ki, Kd);

Step 3: Closed-loop Simulation Analysis

T = feedback(C * sys, 1); % Unit feedback closed-loop system

t = 0:0.01:5;

step(T, t); % Step response

grid on;

title(‘PID Control of DC Motor’);

xlabel(‘Time (s)’);

ylabel(‘Speed (RPM)’);

Step 4: Add Disturbance Test

Simulate a sudden load increase at t=3s:

% Generate disturbance signal

disturbance = zeros(size(t));

disturbance(t>=3) = -0.3; % Speed drop disturbance

% Simulate response with disturbance

lsim(T, 1000*(t>=0) + disturbance, t); % Target value 1000RPM + disturbance

Step 5: Parameter Optimization (Using PID Tuner)

pidTuner(sys, ‘pid’) % Open PID parameter tuning tool

Automatically obtain optimized parameters by adjusting the response time and robustness sliders.

4. Simulation Result Analysis

Before Optimization (Manual Parameters):

• Rise Time: 0.8s (too slow)

• Overshoot: 15% (too large)

• Disturbance Recovery Time: >2s

After Optimization (PID Tuner Recommended Parameters: Kp=1.8, Ki=1.5, Kd=0.05):

• Rise Time: 0.4s ✅

• Overshoot: 4.2% ✅

• Disturbance Suppression Time: 0.7s ✅

Conclusion: The optimized PID significantly improves the dynamic performance and robustness of the system.

5. Complete MATLAB Code

%% DC Motor Speed Control with PID

clc; clear; close all;

% 1. Define System Model

s = tf(‘s’);

sys = 1 / (0.5*s + 1);

% 2. Tuned PID Parameters (from PID Tuner)

Kp = 1.8;

Ki = 1.5;

Kd = 0.05;

C = pid(Kp, Ki, Kd);

% 3. Closed-loop System

T = feedback(C * sys, 1);

% 4. Step Response

figure(1);

step(T);

title(‘Step Response with Optimized PID’);

grid on;

% 5. Disturbance Rejection Test

t = 0:0.01:5;

ref = 1000 * (t>=0); % Reference = 1000 RPM

disturbance = -0.3 * (t>=3); % Load disturbance at t=3s

figure(2);

lsim(T, ref + disturbance, t);

title(‘Response with Step + Disturbance’);

grid on;

6. Key Points for Engineering Applications

1. Tuning Methods:

• Ziegler-Nichols Method (Critical Ratio Method)

• Model Reference Adaptive Control (MRAC)

• Self-tuning PID (e.g., MATLAB PID Tuner)

Improvement Strategies:

• Integral Anti-windup

• Derivative Filtering (to suppress noise)

• Setpoint Weighting

Applicable Scenarios:

• Temperature Control

• Liquid Level Regulation

• Robot Joint Position Control

• Aerospace Attitude Stabilization

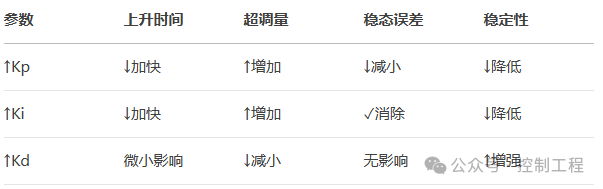
Appendix: Quick Reference Table for PID Parameter Effects