Exploring the Application of Matlab in A Level Mathematics Teaching
AuthorChen JunmingMathematics Teacher at Jiangsu Taizhou High School, Cambridge International A LevelUsing graphics in A Level Mathematics teaching holds significant importance.As A Level Mathematics teaching progresses, teachers find it challenging to draw, prove, and solve complex graphics or teaching tasks quickly using chalk on the blackboard.The traditional teaching methods have long made students feel bored.The emergence of Matlab allows teachers to better utilize modern mathematical software to address the key difficulties in teaching from multiple aspects and angles, broaden students’ horizons, develop their thinking, and enable teachers to become knowledge transmitters. With the aid of new teaching tools, teachers can present more refined theories and more accurate graphical structures to students.1. Matlab and Its FeaturesMatlab, Mathematica, and Maple are three software programs for mathematics.Matlab is increasingly favored by millions of engineers, scientists, and mathematics teachers worldwide due to its powerful capabilities in image visualization, algorithm development, data analysis, and numerical computation.It has grown far beyond these libraries, becoming a powerful tool for visualization, programming, research, engineering, and communication.Advantages of Matlab include cutting-edge algorithms, massive data processing capabilities, and robust programming tools.In secondary education, Matlab’s strong visualization performance provides an excellent mathematical teaching software platform for mathematics teachers, creating an environment for teachers and students to explore the learning of function graphs, geometric relationships, etc. Through Matlab’s graphical display, complex shapes (such as spatial geometric figures and three-dimensional function graphs) can be presented to students using Matlab’s visualization capabilities.2. Application Research of Matlab in High School Function Graphs2.1 Changing Traditional Teaching Models Using MatlabIn the teaching process, through Matlab simulation program images, after determining the teaching objectives, instead of first giving mathematical conclusions, students are encouraged to observe, analyze, compare, and measure data through graphics, allowing them to summarize conclusions while the teacher provides commentary on the mathematics teaching model. 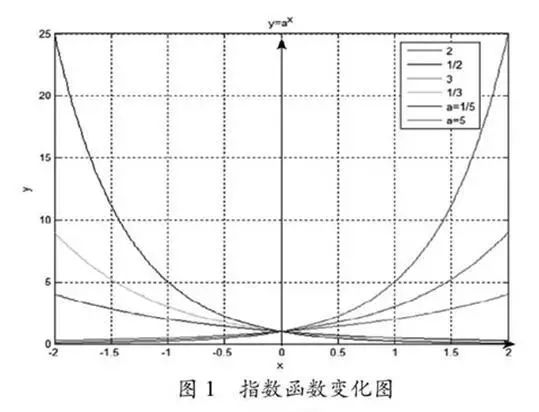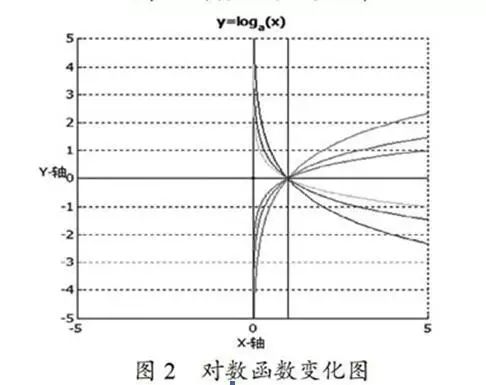Case 1: Comparison of Properties of Exponential and Logarithmic Functions. Teacher: After a brief review of the concepts of exponential and logarithmic functions, demonstrate the exponential function graph dynamically using the program, as shown in Figures 1 and 2. Student: Observing the graph. Teacher: Poses questions regarding the function’s increasing and decreasing nature, and monotonicity. Student: Discusses and provides answers. Teacher: Similarly asks students to analyze the dynamic demonstration image of the logarithmic function (Figure 2) and demonstrates both the exponential and logarithmic functions on the same graph, allowing students to summarize and conclude. Student: Concentrated observation, providing conclusions. 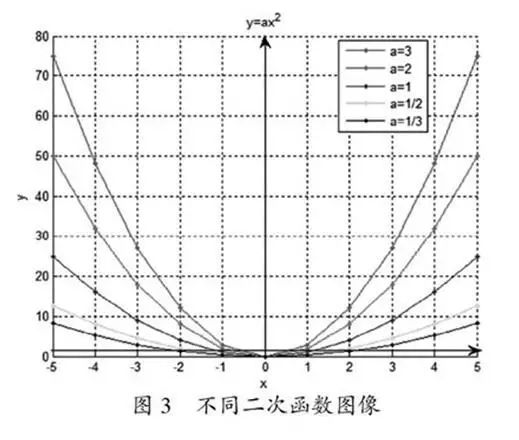Teacher: Summarizes and provides example problems to reinforce the knowledge points.2.2 Expanding Mathematical Knowledge Using MatlabThrough Matlab’s powerful image processing capabilities, simple two-dimensional function graphs can be expanded into three-dimensional space, allowing students to observe and understand the properties of function graphs.Case 2: Graphs of Quadratic Functions and Their ExpansionAfter introducing the basic properties of the quadratic function = (>>0), to discuss and compare the properties of functions, we can obtain comparison result graphs of quadratic curves.Through Figure 3, students are required to analyze the characteristics of the graph, such as vertex, opening, axis of symmetry, increasing and decreasing nature, etc., focusing on analyzing how the size of the opening affects the graph. 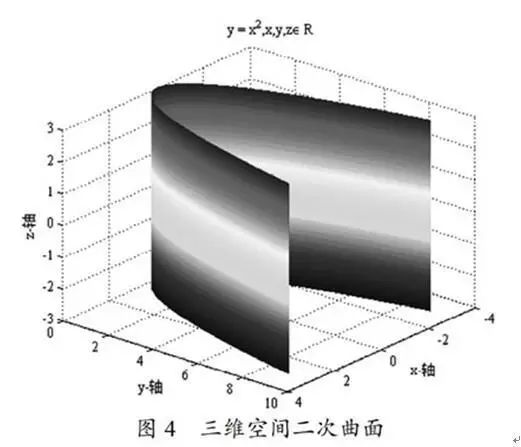Students are required to analyze and summarize the general characteristics of the function.To broaden students’ knowledge, questions are posed for students to consider the graph problem in three-dimensional space = {（） | } in = . Through program design, the image shown in Figure 4 can be obtained.Using Matlab’s built-in image rotation feature, students can observe and analyze the characteristics of the function from different angles in three-dimensional space. 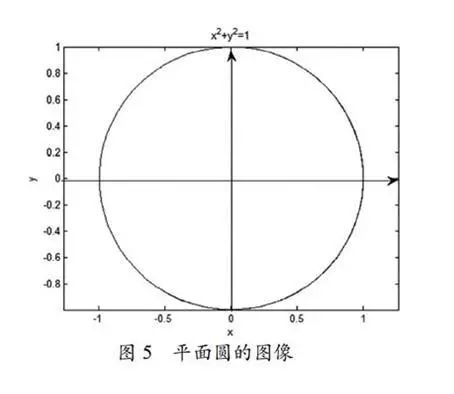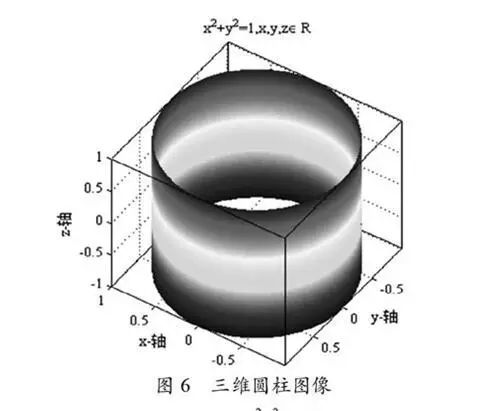The teacher analyzes and summarizes the connections and differences between Figures 3 and 4.Case 3: The Graph of a Circle and Its ExpansionCircleis a fundamental element of various geometric figures. 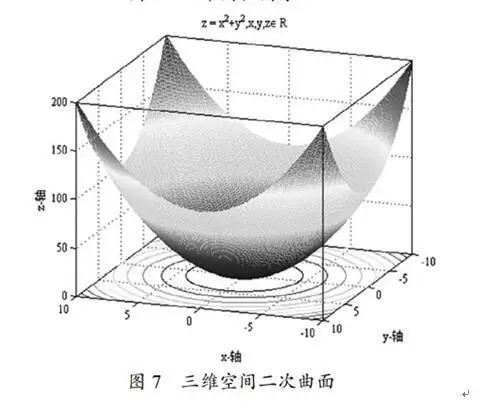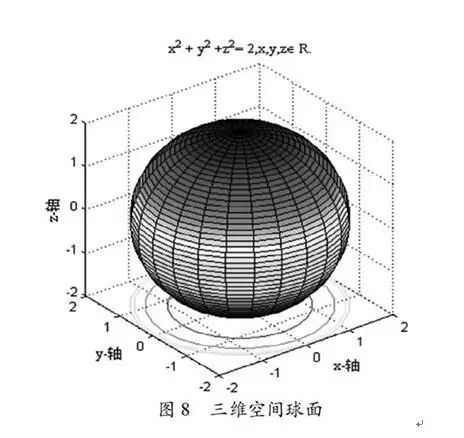By having students recall the basic characteristics of the circle (as shown in Figure 5) + ;= 1, the teacher poses questions about + ;= 1 in three-dimensional space, prompting students to think about the graph of the function in three-dimensional space (as shown in Figure 6).First, through Matlab’s rotation function, allow students to observe Figure 6 from various perspectives, analyzing and comparing the characteristics of the images from different angles. Similarly, demonstrate + ;= , ;+ ;+ ;= 2 in three-dimensional space (Figures 7 and 8), and have students observe and think about them, finally allowing the teacher to provide relevant conclusions.Through the extension of the circle’s graph in space, students gain an understanding of spatial concepts. By imagining geometric shapes from real objects, and then simulating three-dimensional shapes through Matlab, students can analyze geometric figures from different perspectives and decompose complex shapes into basic figures, analyzing the basic elements and their relationships within them. They also learn to recognize the shapes and relative positions of objects seen from different angles, understanding the characteristics of spatial figures like cylinders and spheres.Developing students’ spatial awareness is not isolated; it requires teachers to skillfully use Matlab in the teaching process to organically integrate the characteristics of basic figures, transformations of basic figures, and extensions of figures in three-dimensional space.3. ConclusionGiven the high demands of A Level Mathematics on students’ understanding of graphics, and with the development of modern mathematical software, it is a teacher’s responsibility to master these mathematical software (such as Matlab, Geogebra, etc.) to prepare mathematics lessons better for students.This article explores two roles of utilizing Matlab in high school teaching: one is changing traditional teaching models using Matlab, and the other is expanding mathematical knowledge using Matlab. Through case studies, this article discusses the roles of these two aspects.The teaching effects indicate that students have a strong interest in the expanded graphs of circles in two-dimensional space into three-dimensional space, with enthusiastic observation and discussion, which greatly aids students’ independent thinking abilities, self-summary skills, and spatial concepts.WeChat Official Accountstzjqgjzx
