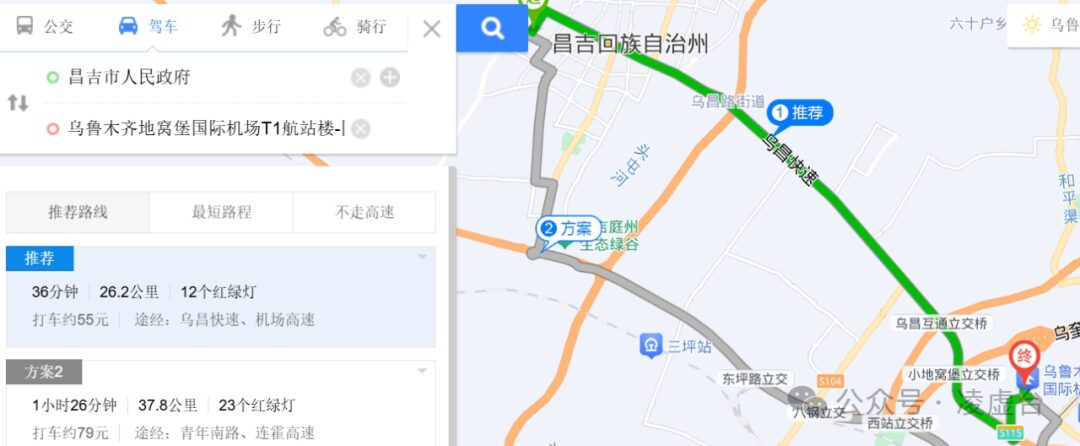
|
city |
jwd |
| Urumqi | 87.480035,43.905793 |
| Kelamayi | 84.957440,45.467231 |
| Turpan | 89.102504,43.031556 |
| Hami | 93.664135,42.843051 |
| Changji | 87.267401,44.014100 |
| Bole | 82.303500,44.898354 |
| Kuerle | 86.142326,41.622753 |
| Aksu | 80.292036,41.263033 |
| Atushi | 76.168400,39.716100 |
| Kashgar | 76.026633,39.542488 |
| Hotan | 79.867859,37.038437 |
| Yining | 81.332453,43.957164 |
| Tacheng | 83.346030,46.672249 |
| Altay | 88.086295,47.751905 |
The above data is sourced from the internet, except for Changji and Atushi, all others are local airport coordinates.
function D=distance(x,y) % Define a function distance that takes two inputs x and y and returns one output Dx=x/180*pi; % Convert each element in the x array (latitude and longitude) from degrees to radiansy=y/180*pi; % Convert each element in the y array (latitude and longitude) from degrees to radians% Here we calculate the sine of half the angular difference between the two points on the sphere, multiplied by the Earth's radiusD=2*asin(sqrt((sin(x(1)-y(1)))^2+... cos(x(1))*cos(y(1))*(sin(x(2)-y(2)))^2))*6371;end % End of function% Initialize a zero matrix D to store distances between citiesD=zeros(length(city));% Iterate over each city in the city listfor i=1:length(city)% Split the current city's latitude and longitude string (assumed to be stored in jwd(i)) by comma and convert to double array% Then flip the array (to place longitude and latitude in the correct order depending on the original data format)x=strsplit(jwd(i),',');x=flip(double(x));% Iterate over each previous city (including itself)for j=1:i% Process the latitude and longitude of the j-th city similarlyy=strsplit(jwd(j),',');y=flip(double(y));% If i equals j, meaning the current city is compared to itself, set distance to 0if i==jD(i,j)=0;% Otherwise, calculate the distance between city i and city j, and store the result in D(i,j) and D(j,i)% Because the distance matrix is symmetric, D(j,i) is also set to the same valueelse D(i,j)=distance(x,y); % The distance function calculates the distance between two pointsD(j,i)=distance(x,y); % Due to the symmetry of the matrix, no need to recalculateend end endD=round(D,2)% a is the found minimum value, b is the index of that minimum value when summing D along the columns[a, b] = min(sum(D));% Use index b to get the corresponding city name from the city arraycityName = city(b);% Display or process the found city namefprintf('The city corresponding to the minimum distance is: %s', cityName);