The mining of Bitcoin has gone through the evolution from CPU to GPU, FPGA, and finally to ASIC. Originally, Satoshi Nakamoto’s intention was “one CPU, one vote,” making Bitcoin mining a democratic and fair process. However, due to the lure of profit, people began using specialized chips to implement the SHA-256 hash algorithm, leaving CPU users with almost no chance of earning block generation rewards, further concentrating what was intended to be decentralized mining into powerful centralized mining pools, rather than the beautiful decentralization originally envisioned.
The schematic diagram of the SHA-256 algorithm is shown below. The function c compresses a 768-bit input into a 256-bit output, and it is a hash function with collision resistance. A variable-length input is divided into many fixed-length 512-bit blocks, and then the function c is iteratively called to obtain the final 256-bit hash value. From this principle, it can be seen that very little storage is required to achieve fast calculations using chips, making it particularly suitable for ASIC implementation.
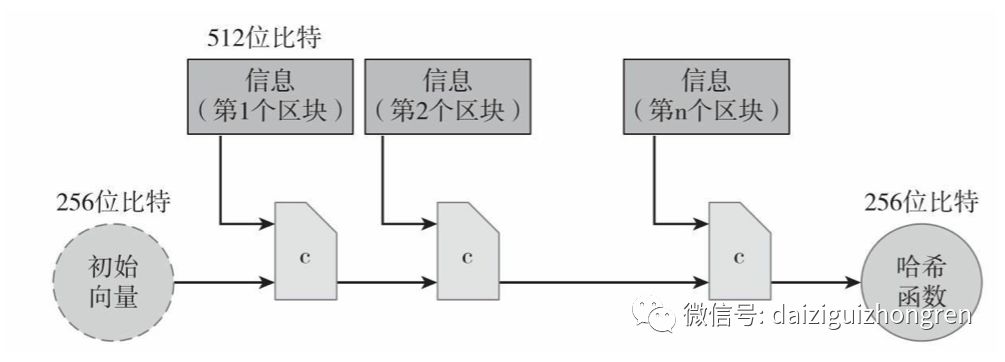
So the question arises, how can we design a new algorithm that is resistant to ASIC?
There is nothing that can stump clever humans; problems always have answers. Litecoin was the first to implement the ASIC-resistant mining algorithm Scrypt, with the core idea being to achieve a balance between computing power (CPU) and memory (RAM). For both ASICs and CPUs, the manufacturing cost and access speed of memory (RAM) are not significantly different. Therefore, Scrypt forces miners to either have large memory to cache intermediate hash results to improve computational speed and efficiency, or if they lack large memory, they must repeatedly compute hashes, consuming significant computational power.
Pseudocode for Scrypt implementation:

From line 9, we can see that V[j] actually uses previously computed SHA-256 hash values stored in memory to reduce a series of SHA-256 calculations, similar to how dynamic programming uses caching to save previously computed states to reduce redundant calculations. If there is not enough large memory (RAM), then the pre-computation done in line 5 cannot be used. In that case, it must be recalculated when needed. V[j] is the SHA-256 computation of the previous V[j-1], and V[j-1] is the SHA-256 computation of the previous V[j-2], and so on. Thus, the time complexity of obtaining V[j] is O(N). Considering the loop from lines 6-9, the overall algorithm, without memory (RAM) caching, has a time complexity of O(N*N) (quadratic); with memory caching, it is O(N) (linear). When N is large, quadratic computation is a time-consuming process, requiring miners to balance memory and computational power, as strong computational power no longer has an advantage.
Satoshi Nakamoto likely started from the assumption that humans are inherently good and adopted the simple SHA-256 for mining; otherwise, they would have certainly used an algorithm like Scrypt that requires balancing memory (RAM) and computational power (CPU). Even masters can miscalculate sometimes.
==================================
Blockchain and Digital Currency
The official blockchain community in waiting — creating a premium community within the blockchain space.

Previous recommendations:
-
Live Broadcast | Opportunities You Don’t Want to Miss in the Blockchain Era
-
Examining the Blockchain Layout of Internet Companies
-
Digital Currency May Be an Illusion
-
Blockchain Traceability and Anti-Counterfeiting, Don’t Be Silly
-
Meal Tickets Are a Scam, But Also a Beginning
-
Understanding DPoS with Pseudocode
-
Technical Questions Must Be Answered for Large-Scale Blockchain Applications
-
Blockchain Revolution, Discussing Mindset, Speculation, and Investment
-
Blockchain Revolution, What Can You Participate In?
-
During Market Crashes, It’s Time to Return to the Essence of Blockchain and Digital Currency