This article is a featured article from the Kanxue Forum.

Author ID on Kanxue Forum: LunaYoung

Talosec Core Team: Wang An, Yang Xiaoya

We conducted a security assessment of an open-source hardware wallet using side-channel analysis.

This wallet’s chip is based on the ARM-Cortex-M4 core, which uses the Elliptic Curve Digital Signature Algorithm (ECDSA) for signing.

With the source code available, we analyzed various methods of side-channel attacks on the ECDSA algorithm, identifying both the locations where side-channel protections have been implemented and areas that may be vulnerable to such attacks, and we attempted to validate our conclusions through experimentation.

Finally, we provided some improvement suggestions for side-channel protection. Our second report, Part 2, will conduct further attack testing on the improved scheme.

Due to the forum’s limitation of inputting mathematical formulas in text format, this report involves a large number of mathematical formulas, and we will upload the analysis report as a PDF attachment.

Introduction

>>>>

1. Research Background and Significance

Unlike most traditional currencies, Bitcoin is a digital currency. Since Bitcoin does not exist in any physical shape or form, it cannot technically be stored anywhere.

During a transaction, both parties need a “Bitcoin wallet” similar to an email account and a “Bitcoin address” similar to an email address. Just like sending and receiving emails, the remitter can directly pay Bitcoin to the recipient’s address using a computer or smartphone.

A Bitcoin address and a private key appear in pairs; their relationship is akin to a bank card number and a password. The Bitcoin address serves as a record of how much Bitcoin you hold at that address.

You can generate Bitcoin addresses at will to store Bitcoin. Each Bitcoin address generates a corresponding private key upon creation. This private key can prove your ownership of the Bitcoin at that address.

We can simply understand a Bitcoin address as a bank card number, with the corresponding private key as the password for that bank card number. Only if you know the bank password can you use the funds associated with that bank card number.

Therefore, the private key is particularly important for a Bitcoin wallet.

Bitcoin wallets can be roughly divided into two types based on how they store private keys: hot wallets and cold wallets.

Hot wallets require an internet connection to use, while cold wallets are used offline, making it significantly harder for external parties to access private key storage via the internet, thus greatly reducing the risk of hacking.

Among cold wallets, hardware wallets are very popular. The private key is stored inside the hardware’s microprocessor, and transactions are confirmed within the hardware wallet, ensuring that even if the computer gets infected with a virus, the keys will not be leaked, providing high security.

Compared to other offline wallets, such as paper cold wallets, hardware wallets stand out for their convenience. They can connect to a computer via USB or Bluetooth, allowing transactions to be confirmed with the click of a button.

During operation, encrypted electronic devices may leak side-channel information such as timing, energy consumption, or electromagnetic radiation. The methods that utilize these leaks to attack encrypted devices are known as side-channel attacks.

Side-channel attack techniques are a hot research direction in international cryptography. They can directly obtain intermediate information from cryptographic computations through physical channels and can segment and recover longer keys, making them easier to attack actual cryptographic systems than traditional cryptanalysis.

Therefore, international mainstream cryptographic product evaluation agencies regard the ability to defend against side-channel attacks as a primary criterion for assessing the security of devices or chips. Scholars and hackers can use side-channel attacks to crack cryptographic modules or security products through methods such as power analysis, electromagnetic radiation attacks, fault attacks, mid-range electromagnetic and sound attacks, and cache attacks.

As a hardware device, a hardware Bitcoin wallet inevitably leaks some side information during computation. For example, during the signing process, the private key is used. If an attacker collects the power or electromagnetic side information at this time, there is a certain probability of obtaining the private key stored in the wallet.

Obtaining the private key essentially equates to completely cracking the electronic wallet, making side-channel analysis of Bitcoin wallets particularly important.

If we cannot prove that a hardware Bitcoin wallet is resistant to side-channel attacks, we have every reason to doubt the security of that wallet.

>>>>

2. Current Research Status at Home and Abroad

Currently, there are various brands of hardware wallets on the market. Although some claim to have defenses against side-channel attacks, they have not disclosed details, so their security remains unknown without third-party evaluation.

On April 30 of this year, Riscure released a report on electromagnetic pulse fault injection experiments on KeepKey, which bypassed its PIN code authentication process and reset private key steps, allowing an attacker to gain access to the wallet’s private keys without entering a PIN.

We typically focus our side-channel analysis on different cryptographic algorithms. For the same algorithm, there are many common issues in its implementation across different hardware devices.

Since the signing algorithm in the Bitcoin wallet we are studying is ECDSA, which is based on ECC, there has been a significant accumulation of side-channel analysis research on ECC both domestically and internationally over the years, primarily involving power analysis and fault injection methods. Below we will introduce these two side-channel analysis methods in ECC.

In terms of power attacks, Coron pointed out in [2] that simple power analysis (SPA) can be performed on the scalar multiplication implementation in ECC.

For the Montgomery algorithm’s modular exponentiation, Herbst indicated in [3] that template attacks (TA) can be executed on this process. Attackers can first conduct multiple experiments on a fully controllable device to build a template, and then collect the energy consumption during encryption on the target device to match against the previously established template.

When computing scalar multiplication, i.e., kP, if k is fixed, the attacker can freely choose P. Thus, the attacker can select multiple values for P, allowing the device to perform encryption operations while collecting the energy consumption during the encryption process. In this case, correlation power analysis (CPA) can be used to recover k a few bits at a time, as mentioned in [4].

In reference [5], the authors proposed a method that lies between SPA and CPA—comparison method. Fouque et al. in [6] pointed out that for two doubling points 2P and 2Q, the attacker may not be able to determine the specific values of P and Q from the energy waveforms, but can learn whether P and Q are equal by comparing waveforms, thus providing an opportunity for the attacker to recover all bits of k by comparing the waveforms of kP and k(2P).

Additionally, in cases where P is selectable by the attacker, if the input P contains zero values (such as (x,0) or (y,0)), regardless of the randomization applied to P, it will always have a coordinate value of zero. During scalar multiplication, this zero value can be leveraged to obtain key information, a method referred to as RPA, proposed by Goubin in [7].

Zero-point value attacks (ZPA) [8] extend RPA; RPA uses special points with zero coordinates for energy attacks, while ZPA uses points with zero values in auxiliary registers during field operations for energy attacks.

Besides power analysis, common side-channel analysis methods also include fault injection, where attackers can use lasers, electromagnetic pulses, or power/clock glitches to induce faults in the attacked device, allowing attackers to obtain output values of interest. Readers can refer to [9] for specific methods.

In ECC, there are primarily three fault injection methods. One is safe-error analysis, a concept proposed by Yen and Joy in [10][11], which points out two types of safe-error analysis attack methods. The C-safe-error attack method refers to inducing temporary faults to determine whether the operation is redundant.

Another method is based on weak curves, proposed by Biehl et al. in [12]. Attackers can change the curve parameters a_6 through fault injection, obtaining weak curves with smaller orders, which allows the recovery of k values through brute force when kP is known.

The third method is differential fault attack (DFA), also proposed by Biehl et al. in [12]. Attackers perform encryption once without fault injection to obtain a correct result, then perform encryption again under fault injection to obtain an incorrect result, and compare the results to potentially gain sensitive information.

>>>>

Background Knowledge

>>>>

1. Elliptic Curve Cryptography

This article introduces some basic concepts of elliptic curves using a prime field as an example.

Let p>3 be a prime number, a,b∈F_P, satisfying 4a_3+27b_2≠0. The elliptic curve defined by a and b on F_P is the set of all solutions (x,y) to the equation y^2=x^3+ax+b, where x,y∈F_P, along with the element representing the point at infinity (denoted as O).

For all P(x,y)∈Fp, P+O=P. Let P_1 (x_1,y_1)≠O, P_2 (x_2,y_2)≠O be two points on the elliptic curve, and P_1≠-P_2, then P_1+P_2=P_3 (x_3,y_3), where in affine coordinates, the point addition and doubling on the elliptic curve are given by:

x_3=λ^2-x_1-x_2

y_3=λ(x_1-x_3)-y_1

Here, when P_1≠P_2, λ=(y_2-y_1)/(x_2-x_1); when P_1=P_2, λ=(3x^2+a)/(2y_1).

Q=kP is the basic operation of ECC (P and Q are points on the elliptic curve, k is an integer), referred to as point multiplication or scalar multiplication. Here, k is the private key; Q is the public key; P is a base point on the elliptic curve.

Knowing k and P makes it easy to compute Q; however, knowing P and Q makes it difficult to determine k. The security of ECC relies on this principle.

>>>>

2. ECDSA

The parameter set D=(q,FR,S,a,b,P,n,h) for ECDSA must satisfy certain conditions.

Its key pair is also generated based on the parameter set. A random number d is selected from [1,n-1], and Q=dG is computed. Here, d is the private key, and Q is the public key.

The ECDSA signing algorithm is as follows:

Algorithm 1: ECDSA Signing

Input: Parameter set D=(q, FR, S, a, b, P, n, h), private key d, message m

Output: Signature (r,s)

1: Select k∈_R [1,n-1]

2: Compute kP=(x_1,y_1), and convert x_1 to integer (x_1 ) ̅

3: Compute r=(x_1 ) ̅mod n. If r=0, jump to step 1

4: Compute e=H(m)

5: Compute s=k^(-1) (e+dr)mod n. If s=0, jump to step 1

6: Return (r,s)

The ECDSA verification steps are as follows:

Algorithm 2: ECDSA Verification

Input: Parameter set D=(q, FR, S, a, b, P, n, h), public key Q, message m, signature (r,s)

Output: Determine if the signature is valid

1: Verify if r and s are integers in the interval [1,n-1]. If any verification fails, return ("Reject this signature")

2: Compute e=H(m)

3: Compute w=s^(-1) mod n

4: Compute u_1=ew mod n and u_2=rw mod n

5: Compute X=u_1 P+u_2 Q

6: If X=∞, return ("Reject this signature")

7: Convert the x-coordinate of X, x_1, to integer (x_1 ) ̅; compute v=(x_1 ) ̅ mod n

8: If v=r, return ("Accept this signature"); otherwise, return ("Reject this signature")

>>>>

3. Scalar Multiplication Algorithm

In ECC, the scalar multiplication kP is the most time-consuming operation. The computation generally converts k into binary form and performs operations primarily involving point addition and doubling, as follows.

Algorithm 3: Point Addition and Doubling to Implement Scalar Multiplication

Input: Point P, a positive integer k=〖(1,k_(n-2),…,k_0)〗_2

Output: [k]P

1: R[0]←P

2: For n-2 downto 0

3: R[0]←2R[0]

4: If k_i=1 then

5: R[0]←R[0]+P

6: Return R[0]

>>>>

4. Width-w NAF Algorithm

Width-w NAF is an extension that uses pre-computed points of NAF. Width-w NAF represents an n-bit integer d, d=∑_(i=0)^(n-1)〖d_w [i]2^i 〗, where d_w [i] is an odd integer and satisfies |d_w [i]|<2^(w-1), meaning that among w consecutive elements, there is at most one non-negative value.

Width-w NAF was independently proposed by different authors in [13][14][15]. The generation algorithm proposed by Solinas in [16] is very simple, and we will briefly describe it.

Algorithm 4: Traditional Width-NAF Algorithm

Input: Window width w, a positive integer d.

Output: NAF_W (d).

1: For i=0 to n

2: If d=1mod2 then

3: d_w [i]←d mods 2^w and d←d-d_w [i]

4: Else

5: d_w [i]←0

6: d←d/2

2: Return d_w [n],d_w [n-1],…,d_w [0]

In step 3, “mods 2^w” refers to the signed residue class of odd d, i.e., {{-2^(w-1)+1,…,-3,-1,1,3,…,2^(w-1)-1}. Therefore, we must pre-compute points P, 3P,…,(2^(w-1)-1)P to represent the residual sequence using pre-computed points, which has 2^(w-2) points.

If d in step 1.1 is not even, then d_w [i] is odd, and has|d_w [i]|<2^(w-1). After step 1.1, d is always divisible by 2^w.

Thus, once d_w [i]=0 holds, the next w-1 bits will all be zero, i.e., d_w [i+1]=d_w [i+2]=⋯d_w [i+1]=0.

>>>>

5. Power Analysis Attacks and Hamming Weight Model

The Hamming weight refers to the number of non-zero symbols in a string of symbols. In a binary representation of a string of symbols, it is the count of 1s.

In chips, all operations are ultimately implemented by the logical state changes of semiconductors between 0 and 1. When the chip operates, the changes in logical states will consume energy at the logic gates while generating electromagnetic radiation.

According to the current semiconductor process technology (mainly referring to CMOS technology), cryptographic chips exhibit different energy consumption when processing logical states 0 and 1, generating electromagnetic radiation of varying intensities. Analysts can obtain some side-channel information related to logical 0 and logical 1 by detecting differences in energy consumption or electromagnetic signals.

Since energy consumption and electromagnetic signals usually reflect the same information, we will focus on energy consumption below.

During the execution of an algorithm, certain operation counts of interest to the attacker will typically be produced. For different operation counts, the energy consumption at the chip’s internal logic gates usually varies. This difference is attributed to several models: Hamming weight model, Hamming distance model, zero-value model, etc.

The operation counts are generally stored in binary form within the chip. For software-implemented algorithms, the transitions of the operation counts corresponding to the registers generally switch from all 0s or all 1s to the binary representation of that operation count, and the resulting energy consumption usually conforms to the Hamming weight model.

That is, we assume that the energy consumption t at a certain moment in the algorithm has a linear relationship with the Hamming weight of the intermediate value y:t=aHW(y)+b

If a is positive, the higher the Hamming weight of the operation count, the lower the energy consumption; if a is negative, the opposite holds.

Platform Setup and Preliminary Observations

>>>>

1. Platform Setup

We used a Lecroy WaveRunner 104Xi-A oscilloscope, self-developed energy signal acquisition probe, Mini-Circuits 1.9MHz low-pass filter, test development board, USB to UART board, and computer to set up the experimental platform, as shown in Figure 1.

Figure 1: Physical Diagram of the Testing Platform

>>>>

2. Preliminary Observations

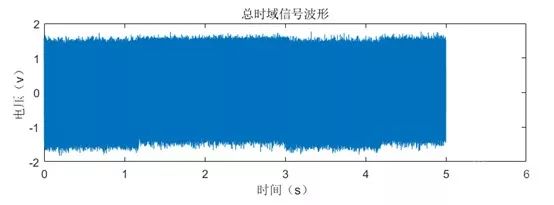
We used a serial debugging assistant to continuously send data to be signed to the chip, with a cycle of 3 seconds, meaning that an ECDSA signing operation is executed every 3 seconds.

During this process, we observed changes in the waveforms on the oscilloscope. It was found that approximately 1.2 seconds of the waveform in each 3-second cycle was quite distinct, significantly different from the energy consumption waveform collected during the chip’s idle state with no instructions sent.

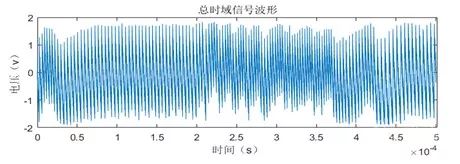
We triggered the serial sending signal and collected 5 seconds of waveforms at a sampling rate of 200KSa/s, resulting in the waveform shown in Figure 2.

Figure 2: Overall Waveform

Knowing that the waveform has a period of 3 seconds, after the initial sampling point, the chip begins processing the received data, so it can be determined that the chip’s signing time is approximately 1.2 seconds. Since the waveform fluctuations are not significant, we applied a smoothing filter with a parameter of 50 to the waveform. The results are shown in Figure 3.

Figure 3: Filtered Overall Waveform

In the 5 seconds captured, two signing operations were clearly visible: the first occurring approximately from 0 seconds to 1.2 seconds, and the second from about 3 seconds to 4.2 seconds.

During the 1.2 seconds of each signing operation, the chip’s data processing can be divided into 5 stages. Stages 1, 3, and 5 are relatively short (less than 0.1 seconds) with significant changes in energy consumption, while stages 2 and 4 each take about 0.5 to 0.6 seconds, are longer, and exhibit relatively minor changes in energy consumption.

Figure 4: Waveforms of Stages 1, 3, and 5 and Their Filtered Versions

We similarly collected and filtered the waveforms for stages 2 and 4 at a higher precision sampling rate, resulting in the outcomes shown in Figure 4.

The waveforms are highly regular, with no significant fluctuations. The waveform for stage 2 includes the waveforms of stages 1 and 3 at the beginning, while the waveform for stage 4 includes the waveforms of stages 3 and 5 at the beginning for easier observation and comparison.

Figure 5: Waveforms of Stages 2 and 4 and Their Filtered Versions

When viewed in detail, the patterns of stages 2 and 4 are almost identical, with the timing being nearly equal. In the ECDSA signing computation process, the most time-consuming operation is the scalar multiplication, which is performed multiple times in a highly regular manner.

According to the source code of the program, the entire signing process includes two scalar multiplication operations: one during the signing for calculating kP, and another for calculating the public key. Thus, it can be inferred that stages 2 and 4 both involve scalar multiplication operations.

It is evident that the waveforms for stages 1 and 3 are quite similar, suggesting that stage 3 corresponds to the computation of s after the scalar multiplication and the process of filling the signature result into the return data format.

We collected the waveforms for stages 2 and 4 at a sampling rate of 500MHz and zoomed in, finding that the waveforms are composed of right-angled triangular shapes, as shown in Figure 6, with a frequency of 32MHz.

We collected a segment of idle phase waveforms (when the chip is waiting for signals from the host computer) at the same frequency and scaled it accordingly, discovering that the idle phase also consists of a similar triangular shape but with a frequency of 24MHz.

The jitter of the right-angled triangular shapes may be caused by display boosting, and we will continue to analyze and conduct noise reduction processing accordingly.

Figure 6: Waveforms of Stages 2 and 4 and Their Filtered Versions

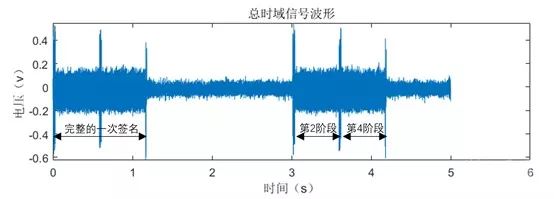
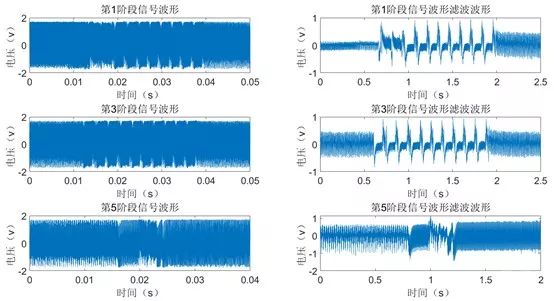
Simple Energy Analysis of the ECDSA Chip

>>>>

1. Introduction to Simple Energy Analysis

At CRYPTO 1999, Kocher et al. proposed the simple energy analysis technique [4], which is based on the assumption that different operations generally have different energy consumption waveforms. Under the current chip manufacturing processes, we believe this holds true.

If the operation sequence relates to parameters or keys of interest to the attacker, the attacker can collect a curve and analyze the changes in the waveform to recover operations during the encryption process, thus deducing keys or related parameters.

>>>>

2. Theoretical Analysis

2.1. Scalar Multiplication Implemented with Traditional Algorithm in Binary

Algorithm 5: Scalar Multiplication Implemented with Traditional Algorithm in Binary

Input: Point P, 256-bit integer k=k_255…k_2 k_1 k_0

Output: kP

Steps:

1: Q=0

2: For j=254 downto 0

3: Q=2Q

4: If k_j=1 then

5: Q=Q+P

6: Return Q

It can be seen that when k_j=1, it corresponds to doubling and adding points, and when k_j=0, it corresponds to doubling points.

Since, in general, the integer k_j has a probability of 1/2 of being either 0 or 1, the ratio of doubling to adding points is approximately 2:1, and there must be a doubling operation before each point addition, while point additions cannot be adjacent.

The attacker can use this basis to distinguish between point additions and doubling points and thereby deduce the value of k.

2.2. Scalar Multiplication Implemented with Width-w NAF Algorithm

In the traditional Width-w NAF algorithm, w is the window length. Before calculating scalar multiplication, the window values(P,2P,…,(2^w-1)P) are pre-stored in memory, and during execution, these point values are directly read from memory.

The algorithm first converts the binary sequence of k into Width-w NAF form before performing scalar multiplication.

Algorithm 6: Scalar Multiplication Using Width-w NAF Algorithm

Input: k, P, w

Output: kP

Pre-computation:

1: Convert k to width-w NAF form, represented as NAF_W (k)=∑_(i=0)^(l-1)▒〖k_i 2^i 〗.

Main computation:

1: Q←∞

2: For i=l-1 downto 1

3: Q=2Q

4: If k_i≠0 then

5: Q←Q+P

6: Return Q

In the Width-w NAF algorithm, when there are more than 4 consecutive zeros, NAF_W (k) indicates that there are more than w consecutive zeros in the representation. In this case, the attacker can recover part of the value of k through waveform analysis.

2.3. Improved Width-w NAF Algorithm Design to Resist Simple Energy Analysis

In the design of the Talosec wallet, the Width-w NAF algorithm was improved based on the scheme proposed in [17].

Grouping k by a window of 4, each group of data forms a 4-bit binary number as an element of array u. If u[i] is 0, then u[i] is assigned the value of 1̅…1̅ (this value is incorrect; for correct representation, please refer to the attachment, and detailed explanation can be found in reference [17]), and the corresponding value is subtracted from u[i+1].

This method ensures that when using the NAF number system constructed in this way to represent k, the scalar multiplication will be fixed operations; that is, for every 4 doubling points, there is one point addition. This helps avoid attacks from simple energy analysis.

Algorithm 7: Anti-SPA Width-NAF Algorithm

Input: w,d

Output: d_w [n],d_w [n-1],…,d_w [0].

1: For i = 0 to ⌈n/w⌉

2: u[i] ←d mod 2^w

3: If u[i]= 0…0 then

4: u[i]←1 ̅…1 ̅ and d←d+2^w.

5: d←d-u[i], d←d/2

6: d_w [iw]=u[i],d_w [iw+1]=…=d_w [iw+w-1]=0.

7: Return d_w [n],d_w [n-1],…,d_w [0]

Then we use the Width-w NAF to compute scalar multiplication, which is identical to the scalar multiplication algorithm using the traditional Width-w NAF algorithm.

2.4. Implementation of Improved Width-w NAF Algorithm to Resist Simple Energy Analysis

The scalar multiplication module of the Talosec wallet adopts the improved Width-w NAF algorithm described in section 4.2.3, where w is 4. For a 256-bit k, theoretically, it uses 64 layers of loops, performing 4 doubling operations and 1 point addition within each loop to process 4 bits of data.

Since each step in this process is a fixed operation that does not leak any information related to the operands, even if the attacker can distinguish between point additions and doubling points from the waveforms, this scalar multiplication algorithm can theoretically resist simple energy analysis.

Observing the implementations of doubling points and point additions in Jacobian coordinates, one can compare their differences; point addition is significantly more complex than doubling points.

In terms of waveforms, if the scalar multiplication portion’s waveform can be analyzed and observed, the data processing analysis should be able to distinguish between doubling points and point additions. Theoretically, doubling points should consume less energy than point additions, and there should be one point addition for every four doubling points.

>>>>

3. Experimental Analysis

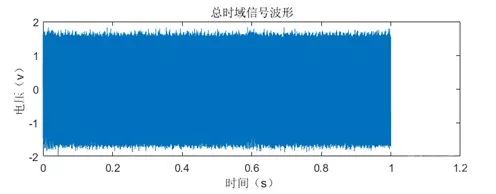
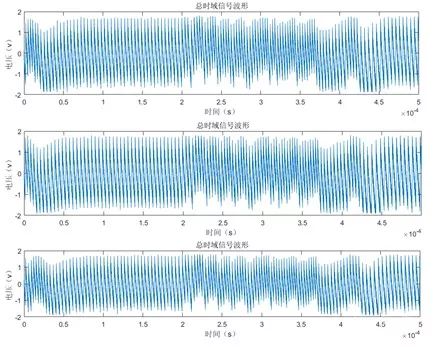
According to the analysis, it can be concluded that the scalar multiplication algorithm ends at approximately 0.6 seconds. We collected waveforms over 1 second at a sampling rate of 10MSa/s, resulting in the waveform shown in Figure 7.

Figure 7: Waveform Containing Scalar Multiplication

We applied smoothing filters with parameters of 2000, 5000, and 10000 to the waveforms and partially zoomed in, resulting in the outcomes shown in Figures 8, 9, and 10.

Figure 8: Scalar Multiplication Waveform with Filter Parameter 2000

Figure 9: Scalar Multiplication Waveform with Filter Parameter 5000

Figure 10: Scalar Multiplication Waveform with Filter Parameter 10000

Upon examining Figures 8 and 9, we can observe that the filtered waveforms indicate that after every four smaller peaks, there follows a larger peak.

Based on statistics, between two larger peaks after filtering, there were a total of 252 smaller peaks and 63 larger peaks, suggesting that the larger peaks correspond to point addition operations. This aligns perfectly with our earlier conclusion that there are 4 doubling points followed by 1 point addition.

From this analysis, we can conclude the following:

(1) Attackers can distinguish between point additions and doubling points from the waveforms through amplification and filtering.

(2) Since the scalar multiplication kP in this wallet employs a fixed-window scalar multiplication algorithm, even if attackers can differentiate between point additions and doubling points, it can effectively resist SPA analysis.

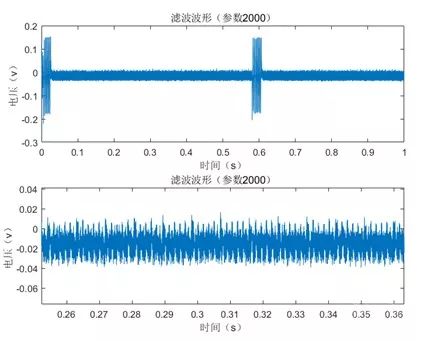
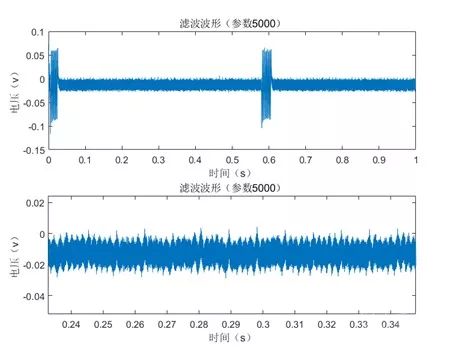
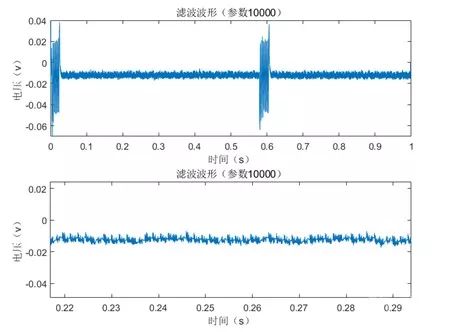
Differential Energy Analysis of the ECDSA Chip

>>>>

1. Introduction to Correlation Energy Analysis

Correlation energy analysis was proposed by Brier et al. at CHES 2004 [18]. Generally speaking, the same operations with different operands correspond to different energy levels.

In the case where the algorithm is known, if an attacker can drive the attacked device to perform encryption multiple times, and the operands involved in the computation with the key are different and known each time, the attacker can use statistical analysis methods on the collected waveforms to recover the key.

People categorize waveforms into several models: Hamming weight model, Hamming distance model, zero-value model, etc. In the case of software implementation, the waveforms typically conform to the Hamming weight model, which we have introduced in section 2.5.

Below, we will briefly introduce the method of correlation energy analysis using the Hamming weight as an example.

In correlation energy analysis, the attacker will perform correlation detection between the waveform point t and the Hamming weight HW(y) of the intermediate value, using the following formula:

ρ=(cov(t, HW(y)))/(σ_t σ_(HW(y)) )=(E[(t-t ̅)(HW(y)-(HW(y)) ̅)])/(σ_t σ_(HW(y)) ).

The mathematical significance of this formula is that if the two vectors are completely positively correlated, then ρ approaches 1; if negatively correlated, then ρ approaches -1; if uncorrelated, then ρ approaches 0.

In performing correlation energy analysis, there are usually two steps: the first is to collect multiple waveforms corresponding to different sensitive intermediate values, and the second is to perform key recovery through guessing the key.

For the waveforms collected during the encryption process, only a portion are truly correlated with the sensitive intermediate values of interest. For evaluators, when the key is known, it is possible to quickly locate leakage points using intermediate value leakage analysis methods.

For attackers, if they have a writable device identical to the target device, they can also locate leakage points using intermediate value leakage analysis methods. Knowing the leakage can significantly reduce the computation needed during the key recovery phase.

1.1. Waveform Collection for Correlation Energy Analysis

Attackers randomly select N plaintexts {P_1,P_2,…,P_N}, encrypt M times, and simultaneously collect M waveforms. The segments of waveforms containing sensitive intermediate value calculations are recorded.

We denote the collected M waveforms as {T_1,T_2,…,T_M}, where each waveform has N points, forming an M by N waveform matrix. The point t_ij in the matrix represents the energy consumption of the i-th waveform at the j-th moment as t_ij.

1.2. Intermediate Value Leakage Analysis Under Known Key Conditions

We know that there exists a moment j at which the j-th column of waveforms{t_1j,t_2j,…,t_Mj} has a significant correlation with the Hamming weights of the sensitive intermediate values during the M encryption processes{HW(y_1),HW(y_2),…,HW(y_M)}.

By iterating over j (1<j<N), we can calculate the correlation coefficients between{t_1j,t_2j,…,t_Mj} and {HW(y_1),HW(y_2),…,HW(y_M)}.

We can obtain N correlation coefficients. Among these N correlations, there should be one moment with a significantly higher correlation coefficient than others. This moment corresponds to the computation related to the sensitive intermediate value.

1.3. Key Recovery Using Correlation Energy Analysis Under Unknown Key Conditions

(1) In the case where the position of the sensitive intermediate value is known

We denote the leakage position as j. First, we guess k=0, using the guessed k with the known M plaintexts to compute the guessed intermediate value y and their Hamming weights, denoted as{HW(〖y^’〗_1 ),HW(〖y^’〗_2 ),…,HW(〖y^’〗_M )}.

Next, we compute the correlation coefficient ρ_0 between{HW(〖y^’〗_1 ),HW(〖y^’〗_2 ),…,HW(〖y^’〗_M )} and {t_1j,t_2j,…,t_Mj,}.

Then we guess k=1 and compute ρ_1; guess k=2 and compute ρ_2; and so on until we compute ρ_255.

If a guess for k is incorrect, the corresponding{HW(〖y^’〗_1 ),HW(〖y^’〗_2 ),…,HW(〖y^’〗_1000 )} will be chaotic random numbers, so ρ_k will be close to 0.

Conversely, if a guess for k is correct, then{HW(〖y^’〗_1 ),HW(〖y^’〗_2 ),…,HW(〖y^’〗_1000 )} will equal{HW(y_1 ),HW(y_2 ),…,HW(y_1000 )}, thus ρ_k will be significantly different from 0.

Therefore, the k corresponding to the most prominent or furthest from 0 ρ_k will be the correct key.

(2) In the case where the position of the sensitive intermediate value is unknown

For the case where the position of the sensitive intermediate value is unknown, for each key guess k, the analyst needs to compute a ρ_k for j points, forming a correlation coefficient curve, denoted as rho_k.

If a correlation coefficient curve rho_k is significantly more pronounced at some point than other curves, it indicates that the corresponding key k is the correct key.

>>>>

2. Theoretical Analysis of the Tested Chip

In this section, we analyze the code for the entire computation process of ECDSA, identifying steps that may be vulnerable to CPA analysis.

2.1. CPA Analysis of Scalar Multiplication Steps

During the attack on the scalar multiplication operation kP, if the attacker can recover k, then during the computation of s=k^(-1) (e+dr)modq, k^(-1) is known. With s, k^(-1), e, and q known, it is easy for the attacker to recover the private key d.

Looking at the code for the scalar multiplication portion, it can be seen that there are two standard methods of generating k. Through analysis, we find that the scalar multiplication steps in this chip can resist CPA analysis for the following reasons:

For the case where k is completely random: The generation of k uses a hardware random number generator, and each waveform uses a different k. The attacker cannot freely choose the value of P, which means the attacker cannot recover k by collecting curves corresponding to different P values.

For the case where k is generated deterministically according to RFC6979: The code shows that Jacobian coordinates are used to compute point addition and doubling. An attacker can fix k using a fixed key and message. If the Jacobian coordinate system uses a fixed z, it theoretically may leak information about k during this signature.

However, in the implementation code, we see that the generation of the coordinate axis z is completely random and uses a hardware random number generator. This means that all intermediate values related to the coordinate values x and y are completely masked during the operation, preventing the attacker from obtaining any useful information through side-channel methods.

2.2. CPA Analysis of the kP Calculation Step for Signature Value

When using ECDSA to perform signing, the signature s requires the private key d, which is one element multiplied by the signature value r. In this step, a fixed unknown private key d participates in the computation with the variable known signature value r.

Computing an operation between a known variable and a fixed unknown number is theoretically feasible for CPA analysis.

We can see the definition of two 256-bit large numbers in the code as shown in Figure 11, and the definition of multiplication for two 256-bit large numbers as shown in Figure 12.

It is observed that the code does not implement protection for the multiplication of the two 256-bit large numbers. We could drive the wallet to perform multiple signatures and collect energy waveforms to conduct correlation energy analysis on the collected waveforms.

Figure 11: Storage Format for 256-bit Large Numbers

Figure 12: Calculation Method for Multiplying 256-bit Large Numbers

Under known key conditions, we can perform intermediate value leakage analysis. Based on the specific implementation method of the algorithm and the bit width of the tested device’s processor, we determine that the number of sensitive intermediate values is 32 bits, totaling 17, which will be analyzed based on the elements of the res array.

For the values involved in the computation, we can obtain the signature value r from the wallet signature return value, while acquiring the private key d from the manufacturer. We can convert the hexadecimal representation provided in the program into the actual large number representation used during computation.

>>>>

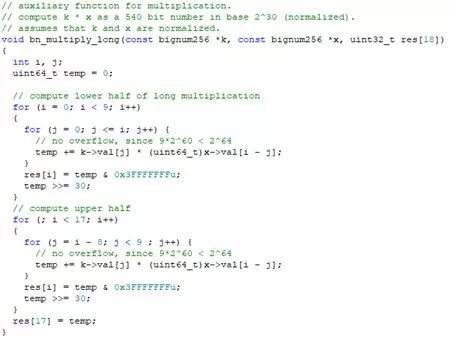
3. Experimental Analysis

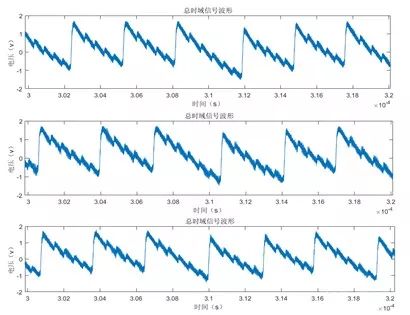
Based on the analysis, we can identify the range corresponding to the d×r analysis step in the overall waveform. We collected 20,000 waveforms for the corresponding range at a sampling rate of 10MS/s, and Figure 13 shows one of the waveforms.

Figure 13: Waveform Corresponding to d×r Step

As shown in Figure 14, we can list multiple waveforms, which exhibit a basic aligned shape.

Figure 14: Comparison of Multiple Waveforms

By selecting a small interval of one waveform for zooming in, we obtain the comparison shown in Figure 15.

Figure 15: Zoomed Comparison of Multiple Waveforms

It can be seen that the waveform exhibits a triangular shape (large) noise, and this noise is not aligned, fluctuating significantly, which can greatly impact the waveform.

For SPA, the influence of this noise can be mitigated through filtering. However, because the operation time for CPA analysis is extremely short, and the signal size is relatively small compared to the triangular noise, excessive filtering will directly eliminate the signals we need.

If we want to eliminate the influence of this noise, we can consider first applying low-pass filtering to the noise and then subtracting the filtered waveform from the original waveform to minimize the impact.

In Figure 16, the top image is the original waveform, the middle image is the result of low-pass filtering with multiple small parameters, and the bottom image is the waveform obtained by subtracting the middle image from the top image.

Figure 16: Eliminating the Influence of Triangular Noise

We performed lateral amplification on the three waveforms in Figure 16, obtaining the results shown in Figure 17. It can be observed that we can effectively eliminate the influence of the regular triangular noise, resulting in denoised waveforms.

Figure 17: Amplified View of the Denoised Waveforms

Using the previously analyzed intermediate values, we conducted leakage analysis on d×r, resulting in the analysis shown in Figure 18.

Figure 18: Analysis Result of Intermediate Value Leakage for the Lowest Byte of d×r

It can be observed that throughout the analysis, the absolute values of the correlation obtained from the intermediate value leakage analysis did not show significant fluctuations. We provide the following conclusions and speculations:

(1) Conducting attack experiments on d×r using the CPA method did not yield effective information.

(2) The inability to recover effective information using CPA does not imply security, as there theoretically exists first-order information leakage; that is, in d×r, d is a fixed unknown key, and r is a variable known signature value. The multiplication process of the two has not incorporated effective side-channel attack defenses.

Thus, theoretically, it does not resist first-order CPA attacks. We speculate that the failure to recover effective information may be due to excessive noise.

To validate the issue of excessive noise, we need to conduct experimental verification of first-order CPA attacks, requiring the following modifications:

(1) Increase the encryption speed to shorten the evaluation process, allowing for the collection of more waveforms for analysis.

(2) Remove the interference of triangular noise.

(3) Modify the circuit board to only collect the energy consumption of the chip.

The above discussions primarily focus on the issue of low signal-to-noise ratio in energy waveforms, as we have already applied amplification and 1.9MHz low-pass filtering to the waveforms, but the results are still unsatisfactory.

If the above three suggestions are difficult to implement, we can consider a different approach: we suggest directly collecting 1 million waveforms for analysis in future work. If 1 million waveforms still do not yield any significant information leakage, we can conclude that the product is secure. However, due to the slow signing speed, this experiment will require some time.

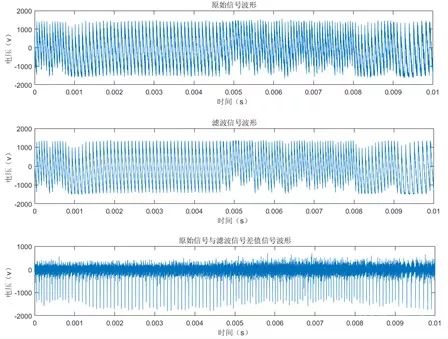
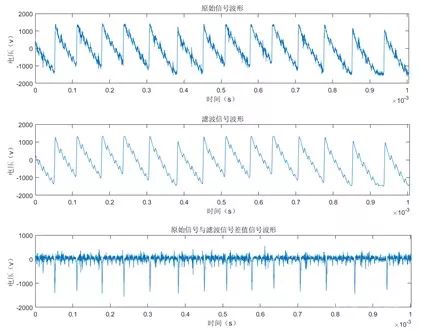
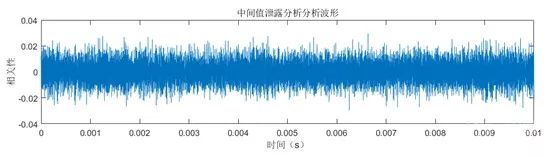
Other Side-Channel Analysis Methods for the ECDSA Chip

Aside from simple energy analysis and correlation energy analysis, we provide a theoretical analysis of the possibility of other side-channel analysis methods attacking this wallet:

1. Referring to the template attack on Montgomery ladder algorithms mentioned by the authors in [3], attackers could theoretically conduct template attacks on the scalar multiplication steps under fixed k conditions. However, the wallet program uses a countermeasure of randomizing the z-coordinate during calculations in Jacobian coordinates, thus avoiding such attacks.

2. When using the improved Width-w NAF algorithm to implement scalar multiplication, the wallet program has optimized the case where the group value is 0, thus resisting safe-error attacks.

3. Theoretically, the kP operation cannot resist a class of fault attacks that map the point kP onto other curves. These fault attacks include the previously mentioned ZPA, RPA, and weak curve attacks. When attackers use these methods to recover k, they can deduce the key d through calculations.

Improvement Suggestions for the ECDSA Chip

1. Without considering circuit design, our theoretical analysis of the implementation process of the d×r step indicates the possibility of CPA analysis. We provide improvement suggestions:

Since

s=k^(-1) (e+dr)modn

 =k^(-1) e+k^(-1) (dr)modn

 =k^(-1) e+(k^(-1) d)rmodn

In the code implementation, this wallet has already randomized k, meaning that a completely random value randk is multiplied with the original value.

Thus, we can first multiply the completely random and unknown k^(-1) with the private key d, and then multiply the result (which is also random and unknown) with the signature value r, thereby avoiding the computation of d×r, eliminating the theoretical possibility of CPA analysis.

2. After completing the kP operation, it is necessary to verify whether the point kP remains on the current elliptic curve to prevent attackers from using fault attacks like ZPA, RPA, and weak curve attacks to recover the k value.

Without considering efficiency, we strongly recommend using the Montgomery ladder algorithm or calculating kP twice to verify whether any faults occurred during the kP calculation.

Summary

International theoretical research indicates that the scalar multiplication algorithm implemented using the improved Width-w NAF algorithm can resist SPA attacks.

At the same time, the project has also employed randomization strategies to defend against template and safe-error attacks, but there still exists the possibility of CPA and fault attacks.

Based on our suggestions, the Talosec project team has made improvements to the potentially vulnerable algorithm points, and has also reinforced the entire security process at the protocol level. We will conduct further tests and analyses on these improved algorithms and protocols in Part 2. Stay tuned.

– End –

Kanxue ID:LunaYoung

https://bbs.pediy.com/user-253538.htm

* This article is original by Kanxue Forum LunaYoung, please indicate that it is from Kanxue Community

The Talosec project practices the open-source spirit, aiming to enhance the security infrastructure of the blockchain world, and is also a project closely linked with the Kanxue Forum. Thanks to the participation and testing of core team members within the forum, the core design and development work of the Talosec wallet has reached a milestone, showcasing the core technical capabilities of the forum.

As security professionals, we have always been exploring the boundaries of security, which will be a mission-driven endeavor—much like the original intention behind the establishment of the Kanxue Forum. Therefore, we hope that more security personnel can participate in this project.

As a symbol of return and technical confidence, we will conduct a priority sale of the product internally within the Kanxue Forum, offering favorable sales plans.

The sale includes two rounds: the first round reserves 0x100 Genesis editions, independently numbered for lifetime free upgrades and replacements, while the second round reserves 0x400 special editions, enjoying one year of free upgrades and replacements (with a one-year warranty for the official version). The pre-sale price is 256 yuan (official retail price is 616 yuan)..

Additionally, we offer other benefits, which you can learn about in the Talosec project commercial white paper (Chapter 3). The technical white paper of the project will be provided later.

Official website: https://talosec.io/

Scan the QR code

Go buy now

Talosec Pre-sale

Lottery Zone

Event Review: Learning Linux Kernel Exploit Vulnerabilities (3)- Bypass-Smep

、

Congratulations Jimu Chutianshu for winning!!

Please send the name of the book and recipient information (recipient, phone number, shipping address) to the WeChat public account backend as soon as possible

Note: If the winning information is not sent within a week after winning, it will be regarded as an automatic forfeiture.

Recommended Articles++++

* Building Your Own PE Interpreter

* HW Action rdpscan Backdoor Simple Analysis

* CVE-2018-0802 Personal Analysis

* Basic Data Type Representations in C++

* Learning Linux Kernel Exploit Vulnerabilities (3)- Bypass-Smep

﹀

﹀

﹀

↙Click the “Read the Original” below to view the original text