IntroductionThis article quickly describes the basic knowledge of elliptic curve algorithms, extending to the principles and practical engineering applications of the commonly used ECIES integrated encryption framework. The aim is to keep it concise, avoiding unnecessary knowledge. A high school level understanding of mathematics is sufficient to read this article. Concepts such as finite fields and cyclic subsets are only briefly touched upon but are explained enough to understand the content of this article. My mathematical foundation is limited, so please correct me if there are any misunderstandings.

Significance of Learning

1.Using shorter keys (e.g., 128bit) can achieve the same encryption strength as RSA (e.g., 1024bit), and the discrete logarithm problem it relies on is more secure than the integer factorization problem that other encryption algorithms depend on, making it one of the widely used encryption algorithms.

2.Elliptic curve encryption algorithms have wide applications in modern encryption systems, banking systems, monetary financial systems, and credential management systems. They provide practical guidance for learning zero-knowledge proofs, blockchain, and encryption system design.

Getting to Know Elliptic Curves

1.Definition of a Circle

A set of points in a plane that are at a constant distance from a fixed point.

2.Definition of an Ellipse

A set of points in a plane where the sum of the distances to two distinct points is constant.

3.Elliptic Curve

An elliptic curve is a binary cubic curve, as shown in the figure below.

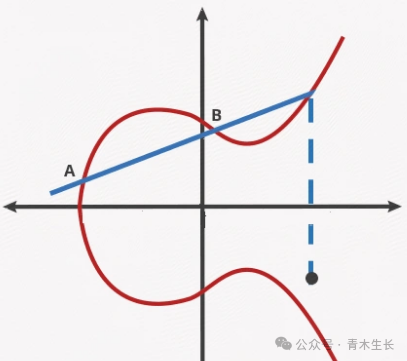
For points on this curve, if defined over the real numbers, it takes the form we learned in elementary mathematics, where the components of the point (x,y) can be decimals or negative numbers.

However, the elliptic curves in cryptography are defined over finite fields, meaning that the points (x,y) belong to a finite set and must satisfy certain properties.

The commonly used form of elliptic curves in cryptography is

, where p is the modulus for division.

We can use the notation

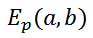
to represent a finite field elliptic curve. For example,

Properties of Elements in Finite Fields

Finite fields are collections of elements and operations constructed to meet certain purposes. For ease of understanding, we can refer to the arithmetic operations of real numbers. Imagine a collection of elements. The elements and operations in this collection satisfy the following characteristics.

1.Support addition and multiplication operations.

2.Support the associative and commutative laws for addition and multiplication.

3.Support the distributive law of multiplication.

4.Each element has an inverse. That is, if element A is multiplied by another element B, the result is the identity element. For example, in the real number field

, in the finite field (assuming the field is: mod(11)), the inverse of element 5 is 9. Because

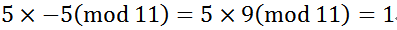
5.Each element has a negative element. That is, if element A is added to another element B, the result is 0. In the finite field (assuming the field is: mod 11), the negative element of 5 is 6. Because

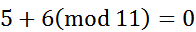
6.Subtraction in finite fields:

, where –b is the negative element of b.

7.Division in finite fields:

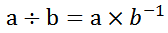
, where b is the inverse element.

8.Note that both the inverse and negative elements must be values within the finite field. That is, for the finite field mod(11), all elements are within the integer range [0-10].

The field mod(11) is a one-dimensional finite field, with elements located in the integer range [0-10]. The elements of a two-dimensional finite field are coordinates of points in a plane, thus points on the elliptic curve within the finite field also satisfy all the properties of element operations mentioned above.

Points on Elliptic Curves

Let’s take a look at the points on the elliptic curve in the finite field.

There is an elliptic curve

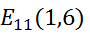
, that is, the curve equation

First, calculate the first point

Let x=2, we get

, and

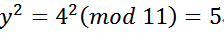
Thus, we know that (2, 4) is a point on the curve. However, it can also be found that

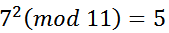
, thus (2, 7) is also a point on the curve. Similarly, points for x=3, x=4, and x=10 can also be calculated. Moreover, the number of these points is finite.

Point Operations on Elliptic Curves

Point Addition

In addition to possessing the properties of finite field elements mentioned above, the point addition on elliptic curves in finite fields is slightly more complex compared to simply adding the components of two points in the familiar real number coordinate system.

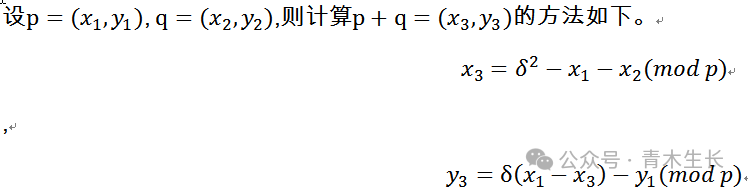
Where

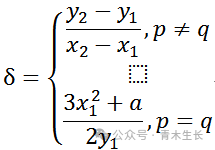
With the groundwork of point addition laid, we can introduce point multiplication.

Point Multiplication

Point multiplication can be implemented in the form of repeated addition, that is,

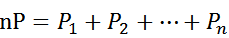
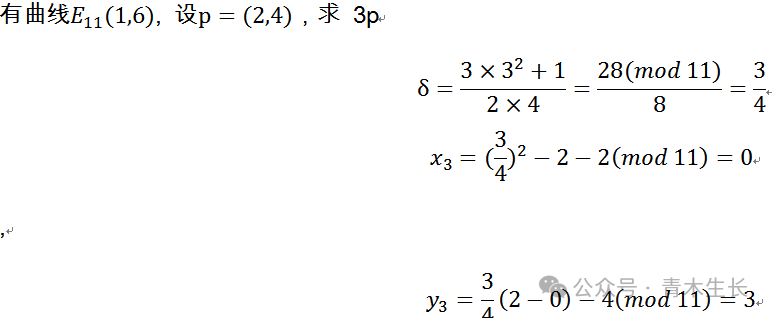
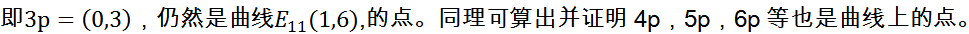
Elliptic Curve Encryption

Similar to the integer factorization problem that RSA encryption relies on, elliptic curve encryption also depends on the computational complexity of mathematical NP problems to resist mathematical attacks. This leads to the elliptic curve discrete logarithm problem. The problem takes the form of point multiplication on elliptic curves in finite fields, that is,

K is a random integer, P and Q are two points on the elliptic curve.

Security of Elliptic Curves

In the above equation (1), the elliptic encryption algorithm uses the integer k as the private key and the point Q as the public key. The mathematical logic behind the security of elliptic curves in finite fields comes from the cyclic set properties of point multiplication operations, where the cyclic results of multiplication arise due to the existence of modular arithmetic. Considering the curve

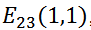
, let

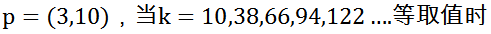
The resulting multiplication of Q is always (6,4), meaning that it is impossible to derive the private key from the public key. The point multiplication operation in finite field elliptic curves has a one-way nature. It is impossible to deduce the exact value of k solely based on Q and P.

Combining this example, given the curve, p point (3,10), Q point (6,4), the derived k value has countless possibilities. When k is chosen to be a very large value, it becomes even more difficult.

Encryption Algorithms

When reviewing articles related to elliptic curves, they include content on both ElGamal and ECElGamal encryption algorithms. Although these two encryption algorithms use different curves, they both incorporate random numbers during encryption calculations, while the random numbers are eliminated during decryption calculations, allowing the plaintext to be recovered in the decryption step.

Stepping out of the topic of elliptic curves, more generally, a curve must meet the following conditions to be used as an encryption curve.

1. The random data added during encryption ensures security. At the same time, this data will be eliminated during the decryption process. Conversely, the method of eliminating random data determines the calculation process for encryption and decryption. This part is the core work in designing encryption curves.

2. To ensure that decryption can proceed normally, operations must be performed within a finite field, which provides a legitimate solution space agreed upon by both the encrypting and decrypting parties. Points that fail to decrypt or cannot be decrypted will fall outside the finite field.

How is the plaintext encoded during encryption?

Another issue is how the plaintext is processed during encryption. Taking the ElGamal algorithm as an example, the algorithm is described as follows.

Since the public key pk is the result of point multiplication, it is a point on the curve. k*pk is also a point after point multiplication, and the plaintext M needs to be encoded and mapped to a point on the elliptic curve to complete the calculation of C2 during the encryption process. Moreover, encoding the plaintext M must ensure that the encoded point is a valid point on the current curve, so it cannot simply be mapped. Existing algorithms such as the Koblitz encoding algorithm can be referenced for study.

Next: ECIES Integrated Encryption Framework and Applications

Previous Reviews#

WeChat Reverse Decryption of Chat Records[With Detailed Steps]

#

Reverse Decryption of a Cloud Security Product Vulnerability Scanning Module Offline Rule Library

#

Exploration of 100% Undetectable Mimikatz

#

Start Your First 0Day Vulnerability Discovery