Click on “Xuan Ge Talks Chips” above to follow for more exciting content!
Many products now implement OTA functionality, allowing for continuous optimization of features and providing users with more functional experiences. Of course, the most important aspect, I guess, is still to solve bug issues.
If a product becomes a bestseller, to avoid being counterfeited, one must also consider how to protect their OTA from being cracked. Back when we developed the balance bike, many copies appeared on the market, even with the same bugs, and they could also download the official app, which was really frustrating. Fortunately, we had backend support that detected the ID range of the counterfeit products and directly issued a “two-dimensional foil” upgrade to them.
When we first started developing products, we considered encryption very little. Implementing OTA functionality is quite simple, but when it comes to protection, there are many aspects to consider. Firstly, the storage of the bin file cannot simply be placed online, and during transmission, plaintext must not appear. Ideally, if the data is intercepted during each update, the encrypted data captured should be different each time, making it sufficiently reliable.
AES is a symmetric encryption mechanism, meaning that the encryption key and decryption key are the same. The two parties in communication agree on this key, using it to package the data during transmission, and then decrypting it with the same key upon receipt. The downside of this encryption method is key storage; if someone else knows the key, it becomes problematic.
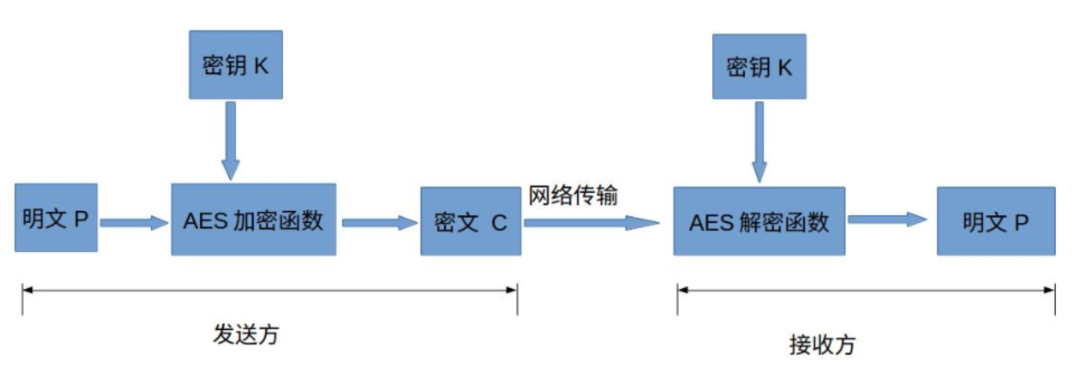
For embedded products, the usual practice is to agree on a product key, which is directly stored securely in the product’s Flash memory, with a copy stored on the server. When the server sends the bin file, it first encrypts it using the key, then transmits it to the product’s main control through various communication methods, where the main control uses the key to decrypt and restore the bin file.
During this process, communication monitoring does not leak the key, so the main protection point becomes the secure storage of the product’s key. In fact, asymmetric encryption methods can be used to first transmit the key for this upgrade to the product’s main control before transmitting the encrypted ciphertext of the key, ensuring that the ciphertext is different each time.
Here, we will first learn about the principles and usage of AES encryption.
1. Basic Structure of AES
AES is a block cipher, which means it divides plaintext into groups of equal length, encrypting one group of data at a time until the entire plaintext is encrypted.
In the AES standard specification, the block length can only be 128 bits, meaning each block is 16 bytes (each byte is 8 bits). The key length can be 128 bits, 192 bits, or 256 bits. Different key lengths recommend different numbers of encryption rounds, as shown in the table below:
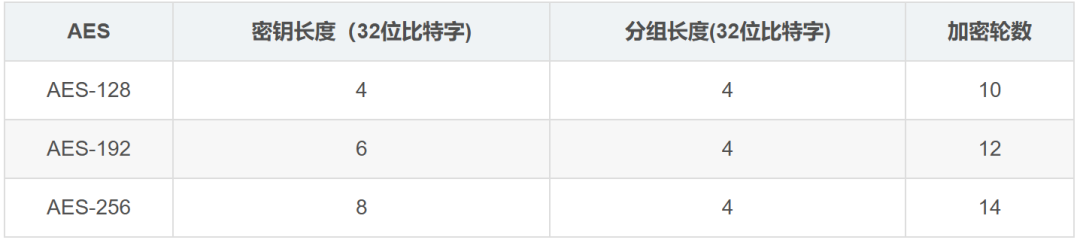
If we implement AES-128 encryption, the recommended number of encryption rounds is 10.
The encryption formula for AES is C = E(K,P), where the encryption function E executes a round function and performs this round function 10 times. The first 9 executions of this round function are the same, with only the 10th being different. This means that a plaintext block will be encrypted for 10 rounds. The core of AES is to implement all operations within one round.
The processing unit of AES is a byte, 128 bits, or 16 bytes, which is the block length. We divide the plaintext into multiple groups of this length.
Each block P and input key K are both 16 bytes, denoted as P = P0 P1 … P15 and K = K0 K1 … K15.
Generally, plaintext blocks are described using a square matrix of bytes, called the state matrix. In each round of the algorithm, the contents of the state matrix continuously change, with the final result output as ciphertext. The arrangement of bytes in this matrix is from top to bottom, left to right.
Assuming the plaintext block is P = abcdefghijklmnop, where the character a corresponds to P0 and p corresponds to P15. As shown in the figure below:
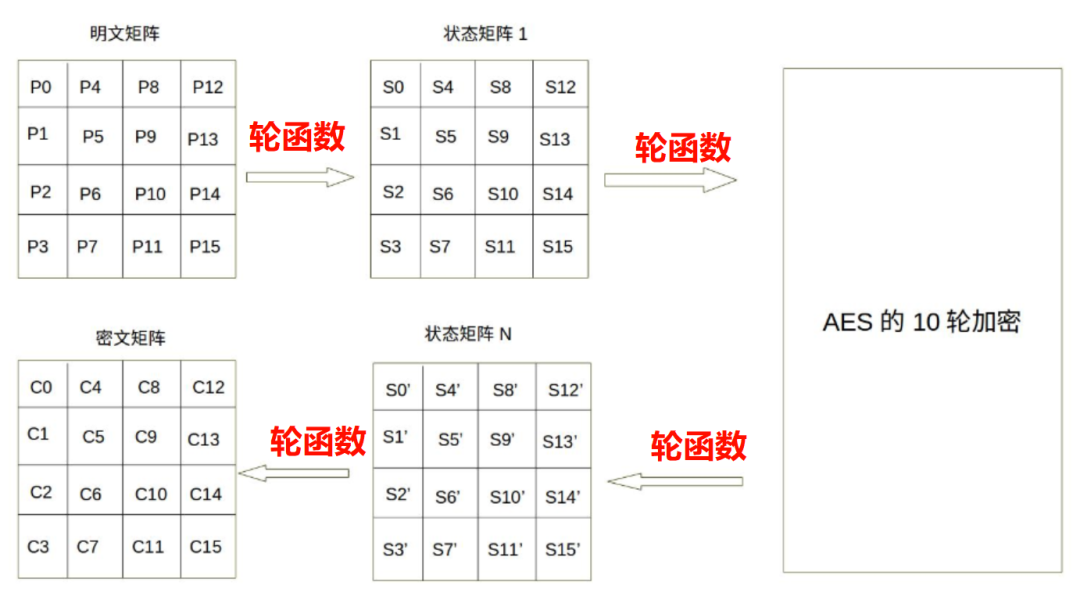
The above figure shows that the plaintext matrix is transformed into a ciphertext matrix after each round function operation. Based on the above plaintext assumption, the data changes significantly during the encryption process, as shown in the figure below:
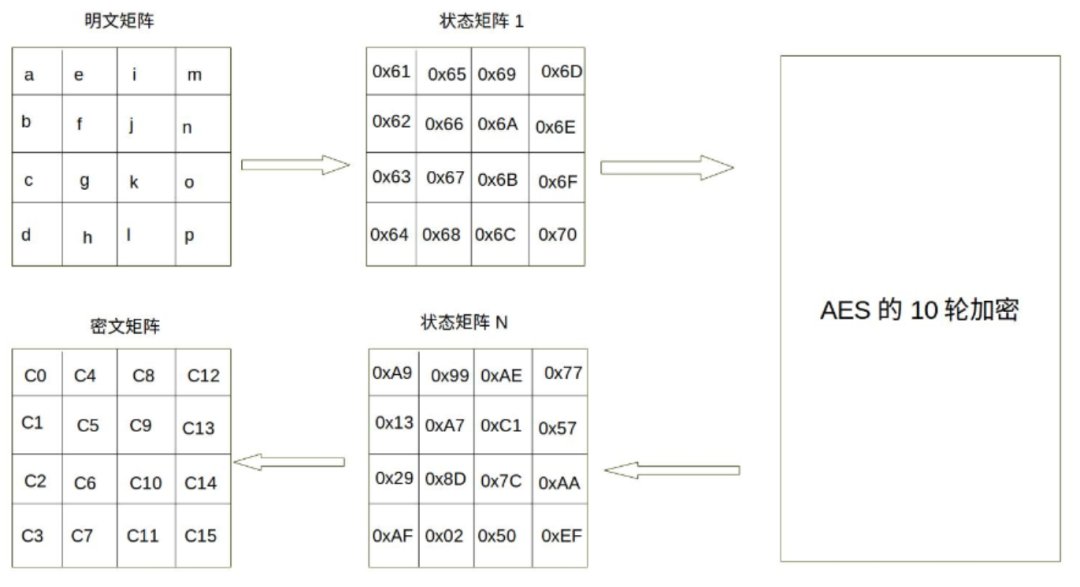
The above part can be simply understood as follows: we first group the plaintext, encrypting 16 bytes at a time, and each encryption consists of 10 rounds. During these 10 rounds of encryption, the plaintext is transformed by the round function 10 times.
2. The Life of a Key
How does the key work? The key is actually divided into 10 parts, with each execution of the round function allowing the key to act on the corresponding round’s state matrix. This means that as the plaintext changes 10 times, 10 different keys are used for 10 actions, and of course, these 10 different keys are all derived from the original key.
The 16-byte key is also represented as a matrix of bytes, with each column referred to as a 32-bit word.
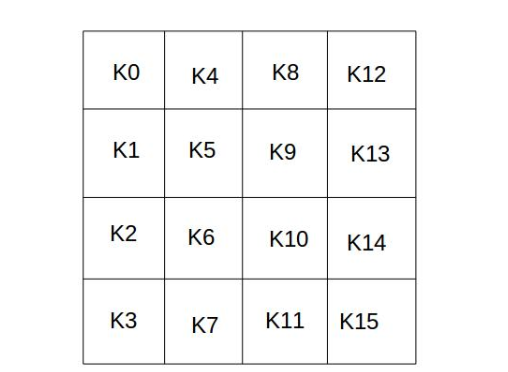
Through the key schedule function, this key matrix is expanded into a sequence of 44 words: W[0], W[1], …, W[43].
The first four elements of this sequence, W[0], W[1], W[2], W[3], are the original key, used as the initial key in the encryption operation; the remaining 40 words are divided into 10 groups, with each group containing 4 words (128 bits) used for the round keys in the 10 rounds of encryption, as shown in the figure below:
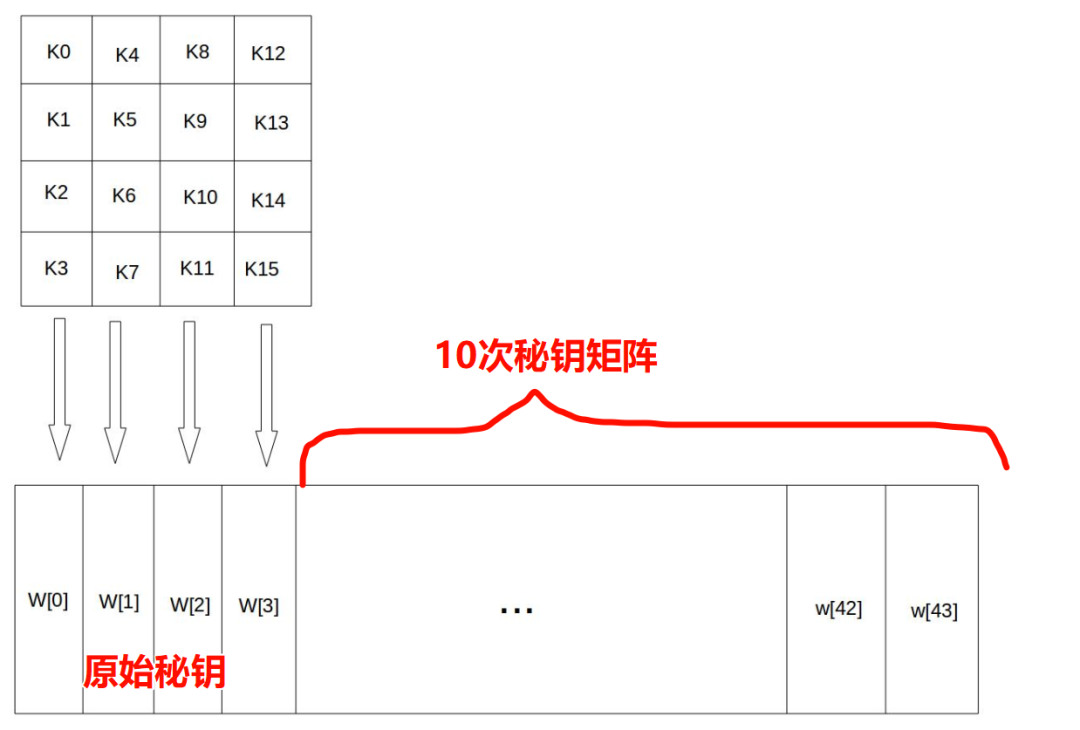
In the figure, if Key = “abcdefghijklmnop”, then K0 = a, K15 = p, W[0] = K0 K1 K2 K3 = "abcd"
The subsequent 10 key matrices are expanded through the key expansion function, as shown in the figure below:
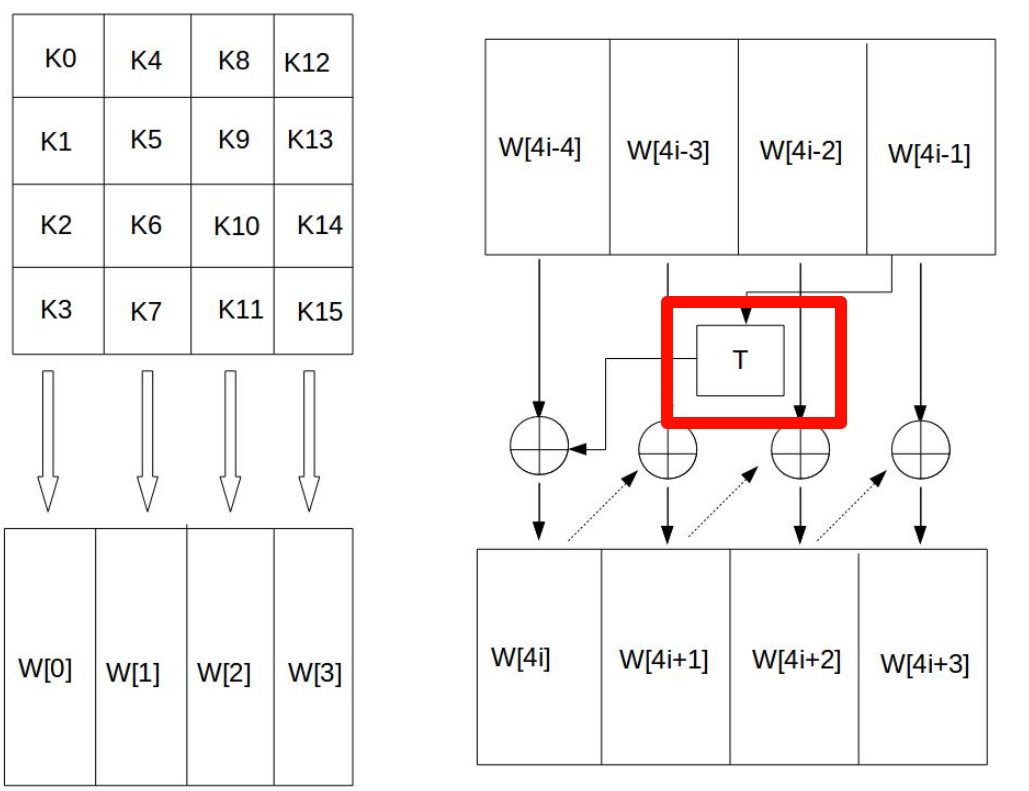
Here, T is a somewhat complex function, similar to the processing of the previous plaintext, calculated through various substitutions and XOR operations. The purpose is to scramble the data, making it appear random.
3. The Encryption Process
W[0,3] refers to the concatenation of W[0], W[1], W[2], and W[3] to form a 128-bit key. The round functions from the 1st to the 9th rounds are the same, including four operations: byte substitution, row shifting, column mixing, and round key addition. The last round does not perform column mixing.
Additionally, before the first round iteration, the plaintext and the original key undergo an XOR encryption operation. Below is a process for AES encryption and decryption.
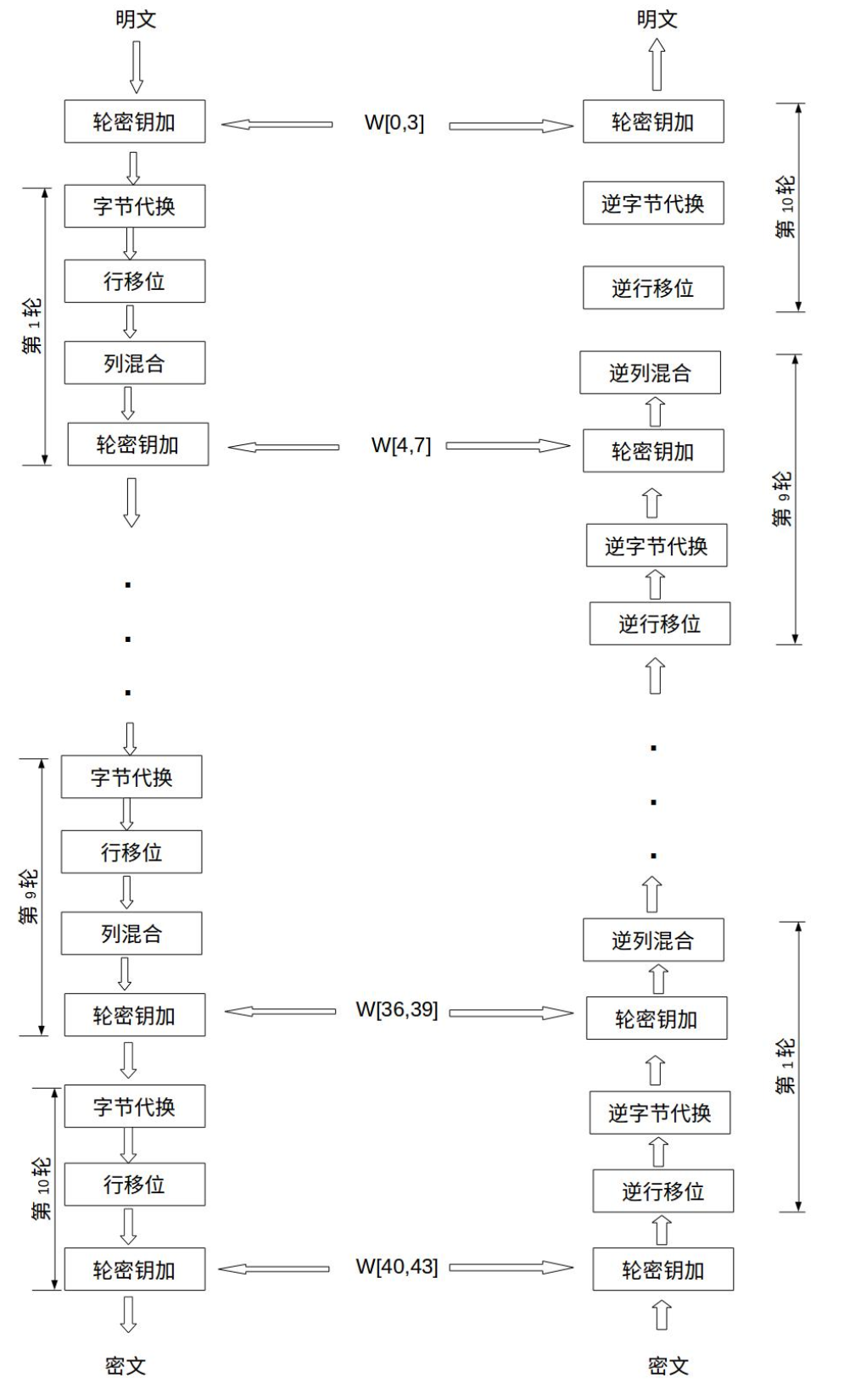
Below is a brief description of the encryption process, providing a general understanding of what needs to be done during encryption and decryption.
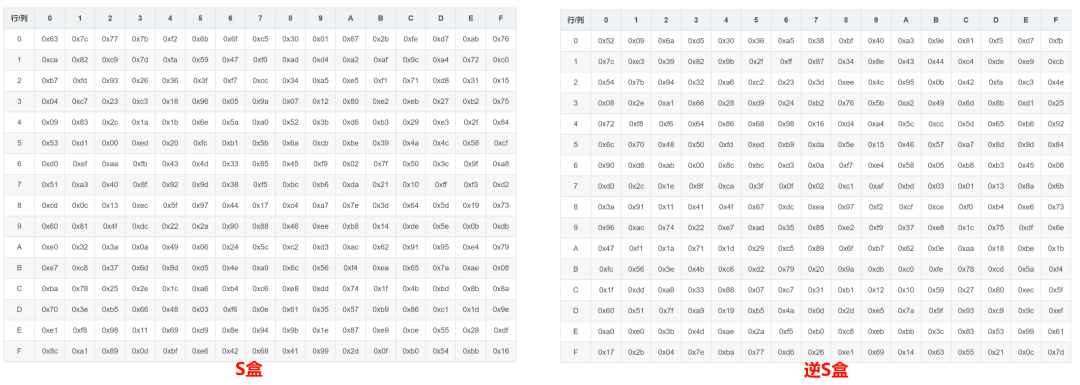
Byte substitution involves a lookup table, where both the encryption and decryption processes require a pair of data tables, known as the S-box and inverse S-box. Essentially, this is a two-dimensional array where data is substituted based on coordinates, and they are reversible during the round encryption process.
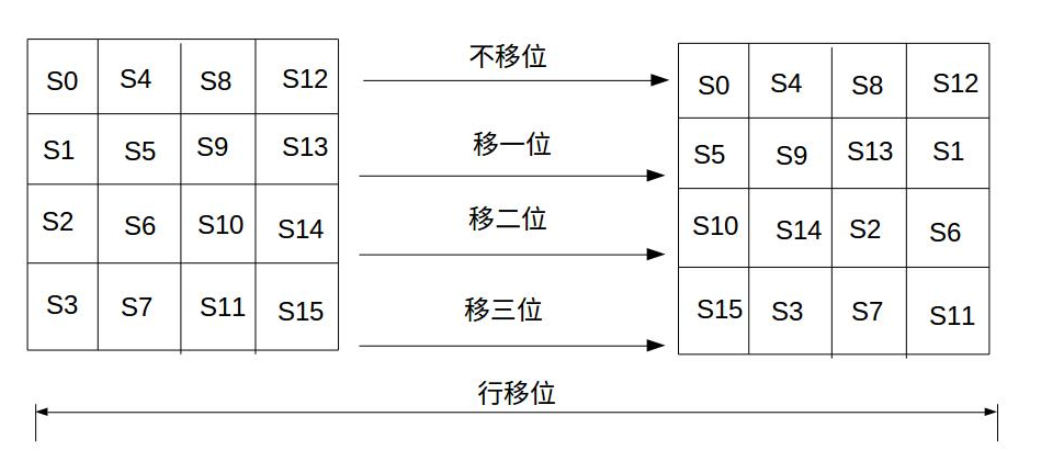
Row shifting is a simple left circular shift operation. When the key length is 128 bits, the 0th row of the state matrix shifts left by 0 bytes, the 1st row shifts left by 1 byte, the 2nd row shifts left by 2 bytes, and the 3rd row shifts left by 3 bytes, as shown in the figure below:
The inverse transformation of row shifting involves performing the opposite shift operation on each row of the state matrix. For example, in AES-128, the 0th row shifts right by 0 bytes, the 1st row shifts right by 1 byte, the 2nd row shifts right by 2 bytes, and the 3rd row shifts right by 3 bytes.
Column mixing also involves a pair of matrix operations, where the product of the two column mixing matrices is the identity matrix. During both encryption and decryption processes, they are also reversible operations.
Round key addition is where we finally use our key matrix.
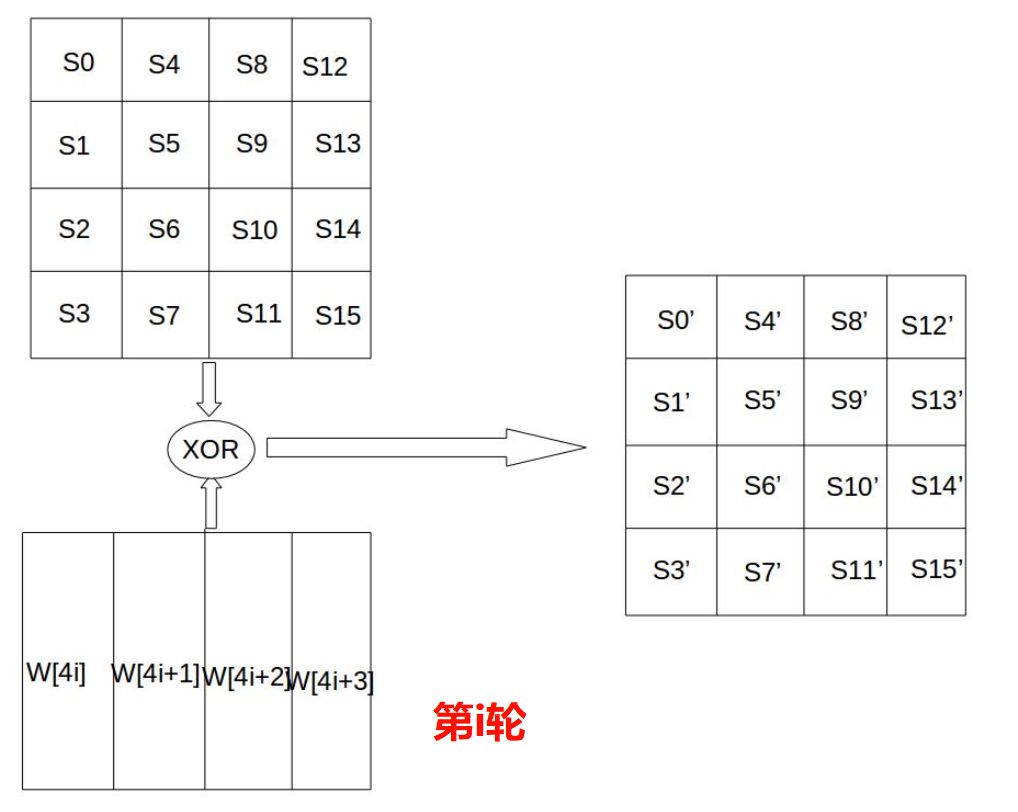
Round key addition involves performing a bitwise XOR operation between the 128-bit round key Ki and the data in the state matrix, as shown in the figure below. Here, each word in the key Ki, W[4i], W[4i+1], W[4i+2], W[4i+3], is a 32-bit word containing 4 bytes. The generation algorithm for these will be introduced below.
The specific algorithm will be published after testing is completed.

Previous Recommendations
Analysis of the automatic download principle of ESP32
Practical article on Bluetooth development for treadmills and rowing machines
Using Bluetooth FTMS protocol to connect with Wanlu or Zwift
How to connect a bridge circuit?
How does a bridge improve sampling accuracy?
What is a Wheatstone bridge? Why use a Wheatstone bridge to measure strain gauges?
Introduction to strain gauges
How is the SEGGER RTT output format defined?

“Read the original text to see more articles from the author. If you think it’s well written, please give it a thumbs up or “look at it”. It would be best to add a star.