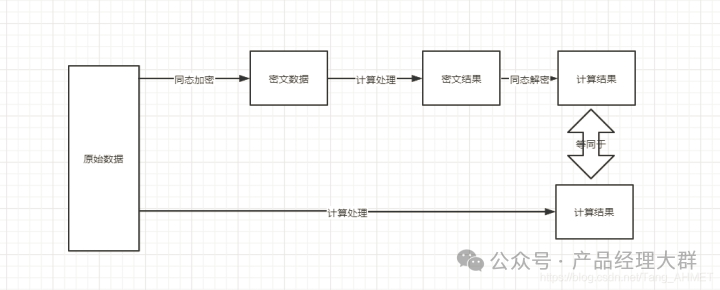
Homomorphic encryption (HE) is a special encryption mode in cryptography that satisfies the property of homomorphic operations on ciphertexts. This means that after data is homomorphically encrypted, specific calculations can be performed on the ciphertext, and the result of these calculations, when subjected to corresponding homomorphic decryption, will be equivalent to performing the same calculations directly on the plaintext data, achieving “computable but invisible” data. The implementation effect of homomorphic encryption is shown in the figure below.
Add image caption, no more than 140 characters (optional)
Homomorphic encryption allows us to send encrypted ciphertext to any third party for computation without needing to decrypt it beforehand, i.e., performing calculations on the ciphertext. Although the concept of homomorphic encryption first appeared 30 years ago, the first fully homomorphic encryption framework that supports arbitrary operations on ciphertext was proposed later, in 2009, by Craig Gentry.
The mathematical definition of homomorphic encryption is as follows:
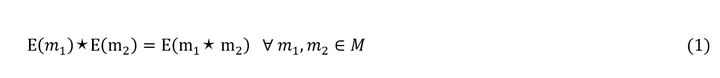
Add image caption, no more than 140 characters (optional)
Where E is the encryption algorithm, and M is the set of all possible information. If the encryption algorithm E satisfies formula (1), we say that E conforms to the properties of homomorphic encryption under the ★ operation. Currently, homomorphic encryption algorithms mainly support two types of homomorphism: addition and multiplication.
It is important to note that the above formula (1) is only to help us better understand the properties of homomorphic encryption; actual homomorphic encryption algorithms may differ. For example, the Paillier algorithm supports additive homomorphism, so according to formula (1), the sum of its ciphertext should equal the sum of the ciphertexts, but in reality, the product of the ciphertext equals the sum of the ciphertexts. Therefore, we generally only require that the resulting ciphertext matches our expected computation, without specific requirements on the calculations performed on the ciphertext (which are generally determined by the encryption algorithm).
Homomorphic encryption algorithms can be divided into fully homomorphic encryption and partially homomorphic encryption algorithms.
-
If a homomorphic encryption algorithm supports arbitrary forms of computation on ciphertext, it is called Fully Homomorphic Encryption (FHE);
-
If it supports only partial forms of computation on ciphertext, such as supporting only addition, only multiplication, or supporting a limited number of additions and multiplications, it is called partially homomorphic encryption, abbreviated as SWHE (Somewhat Homomorphic Encryption) or PHE (Partially Homomorphic Encryption).
Generally speaking, since arbitrary computations can be constructed through addition and multiplication, if an encryption algorithm satisfies both additive and multiplicative homomorphism, it can be said to satisfy full homomorphism.
Currently, homomorphic encryption algorithms have been implemented in scenarios such as blockchain and federated learning, where there is a demand for data privacy computing. However, fully homomorphic encryption is still in the exploratory stage, and existing algorithms face performance issues such as low operational efficiency, large key sizes, and ciphertext explosion, making it challenging to achieve feasible engineering applications.
Therefore, homomorphic encryption algorithms used in practical applications often select partially homomorphic encryption (such as additive homomorphism) to achieve limited homomorphic computation functions in specific application scenarios.
1) Standardization of Partially Homomorphic Encryption
In May 2019, the International Organization for Standardization (ISO) released the homomorphic encryption standard (ISO/IEC 18033-6:2019). This standard only involves partially homomorphic encryption and specifically includes two relatively mature partially homomorphic encryption mechanisms: ElGamal multiplicative homomorphic encryption and Paillier additive homomorphic encryption, and specifies the parameters and key generation, data encryption, ciphertext decryption, and ciphertext homomorphic operation processes for participating entities.
(2) Standardization of Fully Homomorphic Encryption
In July 2017, researchers from academia, industry, and government in related fields formed the HomomorphicEncryption.org open alliance for the standardization of fully homomorphic encryption. They held the first fully homomorphic encryption standardization seminar at Microsoft Research, beginning the collaborative drafting of the fully homomorphic encryption standard, and published three white papers on fully homomorphic encryption security standards, API standards, and application standards. To date, HomomorphicEncryption.org has held five fully homomorphic encryption standardization meetings over three years, with participants including companies such as Microsoft, Samsung SDS, Intel, IBM, Google, Mastercard, as well as representatives from institutions like NIST and ITU, and scholars from major universities. In terms of standardization progress, HomomorphicEncryption.org has released and updated the fully homomorphic encryption standard draft in March and November 2018, respectively.
Among common homomorphic encryption algorithms, the Paillier algorithm and Benaloh algorithm only satisfy additive homomorphism, while the RSA algorithm and ElGamal algorithm only satisfy multiplicative homomorphism, and the Gentry algorithm is fully homomorphic.
Encryption algorithms that satisfy limited operational homomorphism but do not satisfy arbitrary operational homomorphism are called partially homomorphic encryption. Typical characteristics of partially homomorphic encryption include multiplicative homomorphism, additive homomorphism, and limited fully homomorphic properties.
(1) Multiplicative Homomorphic Encryption Algorithms
In practical applications, the demand for multiplicative homomorphism is not common, so multiplicative homomorphism typically exists incidentally in existing classical encryption algorithms. Typical encryption algorithms that satisfy multiplicative homomorphic properties include the RSA public key encryption algorithm proposed in 1977 and the ElGamal public key encryption algorithm proposed in 1985.
① RSA Algorithm
The RSA algorithm is the most classic public key encryption algorithm, with a history of over 40 years, and its security is based on the difficulty of factoring large integers. In practical applications, the RSA algorithm can use padding modes such as RSA_PKCS1_PADDING and RSA_PKCS1_OAEP_PADDING, and based on key lengths (commonly 1024 or 2048 bits), it pads plaintext blocks. Only the original RSA algorithm, which does not pad plaintext, can satisfy the multiplicative homomorphic property. Since the original RSA is not a randomized encryption algorithm, meaning that no random factors are used during the encryption process, the result of encrypting the same plaintext with the same key is fixed. Therefore, using the multiplicative homomorphism of RSA to implement homomorphic encryption operations has security weaknesses, as attackers may obtain the original data through chosen plaintext attacks.
② ElGamal Algorithm
The ElGamal algorithm is a public key cryptographic algorithm based on the difficulty of the discrete logarithm problem in the Diffie-Hellman key exchange, which can achieve public key encryption and digital signature functions while satisfying the multiplicative homomorphic property. ElGamal is a randomized encryption algorithm, meaning that even if the same key is used to encrypt the same plaintext, the resulting ciphertext will be different, thus avoiding the chosen plaintext attack issues similar to those of the RSA algorithm. It is the only specified multiplicative homomorphic encryption algorithm in the ISO homomorphic encryption international standard.
(2) Additive Homomorphic Encryption Algorithms
Paillier Algorithm
The Paillier algorithm, proposed in 1999, is a public key encryption algorithm based on the composite residuosity problem and is currently the most commonly used and practical additive homomorphic encryption algorithm. It has been implemented in many application scenarios with homomorphic encryption needs and is also the only specified additive homomorphic encryption algorithm in the ISO homomorphic encryption international standard. Additionally, since it supports additive homomorphism, the Paillier algorithm can also support scalar multiplication homomorphism, meaning it can support multiplication of ciphertext with plaintext.
(3) Limited Fully Homomorphic Encryption Algorithms
The Boneh-Goh-Nissim scheme proposed in 2005 is a public key cryptographic scheme based on bilinear maps, supporting arbitrary additive homomorphism and one multiplicative homomorphic operation. The additive homomorphism in the scheme is based on ideas similar to the Paillier algorithm, while the one multiplicative homomorphism is based on the properties of bilinear mapping. Since bilinear mapping operations change the group of the ciphertext, it can only support one multiplicative homomorphic operation, but it still supports further additive homomorphic operations on the ciphertext after multiplication.
Encryption algorithms that satisfy arbitrary operational homomorphism are called fully homomorphic encryption. Since any computation can be constructed through addition and multiplication gates, an encryption algorithm is said to satisfy full homomorphism as long as it satisfies both multiplicative and additive homomorphic properties.
(1) Mainstream Algorithms
The development of fully homomorphic encryption algorithms originated from the scheme proposed by Gentry in 2009, and subsequent schemes are mostly based on lattice algebra structures. Currently, fully homomorphic encryption algorithms implemented in mainstream open-source libraries include the BGV scheme, BFV scheme, and CKKS scheme.
① First Generation Fully Homomorphic Encryption Scheme – Gentry Scheme
The Gentry scheme is a fully homomorphic encryption algorithm based on the circuit model, supporting both additive and multiplicative homomorphic operations on each bit. The basic idea of the Gentry scheme is to construct a homomorphic encryption algorithm that supports a limited number of homomorphic operations and introduce the “Bootstrapping” method to control noise growth during the operation process, which is also the mainstream model of the first generation of fully homomorphic encryption schemes. The “Bootstrapping” method transforms the decryption process itself into a homomorphic operation circuit and generates new public and private key pairs to encrypt the original private key and the noisy original ciphertext, then uses the ciphertext of the original private key to perform the homomorphic operation of decrypting the ciphertext of the original ciphertext, thus obtaining a new ciphertext without noise. However, since the decryption process itself is very complex, it generates a lot of noise during the operation. To reserve enough noise growth space for at least one multiplicative operation, it is necessary to compress and simplify the pre-decryption circuit, meaning that some operations in the decryption process should be completed as much as possible during encryption.
② Second Generation Fully Homomorphic Encryption Scheme – BGV/BFV Scheme
The second generation of fully homomorphic encryption schemes after the Gentry scheme is usually based on the LWE/RLWE assumption, with security based on difficult problems in algebraic lattices. Typical schemes include the BGV scheme and BFV scheme.
The BGV (Brakerski-Gentry-Vaikuntanathan) scheme is currently the most efficient scheme among mainstream fully homomorphic encryption algorithms. In the BGV scheme, both ciphertext and keys are represented as vectors, and the product of ciphertext and the corresponding key product is a tensor, so the multiplication of ciphertext causes an explosive growth in the dimensions of the ciphertext, leading to the scheme being able to perform only a constant number of multiplicative operations. The BGV scheme uses key exchange technology to control the dimensional explosion of ciphertext vectors, restoring the expanded dimensions of ciphertext back to the original dimensions after performing ciphertext calculations. At the same time, the BGV scheme can use modulus switching technology to replace the “Bootstrapping” process in the Gentry scheme to control the noise growth generated by homomorphic operations on ciphertext without needing to implement complex decryption circuits. Therefore, after each multiplication operation on ciphertext, it is first necessary to reduce the dimensions of the ciphertext through key exchange technology, and then reduce the noise of the ciphertext through modulus switching technology, allowing for further calculations to continue.
The BFV (Brakerski/Fan-Vercauteren) scheme is another second-generation fully homomorphic encryption scheme similar to the BGV scheme, which can also be constructed based on LWE and RLWE. The BFV scheme does not require modulus switching for noise control of ciphertext, but it also needs to solve the dimensional explosion problem of ciphertext multiplication through key exchange.
Currently, the two most mainstream fully homomorphic encryption open-source libraries, HElib and SEAL, implement the BGV scheme and BFV scheme, respectively.
③ Third Generation Fully Homomorphic Encryption Scheme – GSW Scheme
The GSW (Gentry-Sahai-Waters) scheme is a fully homomorphic encryption scheme based on approximate feature vectors. This scheme is based on LWE and can be extended to RLWE, but its performance is not as good as that of other RLWE-based schemes like BGV. The ciphertext of the GSW scheme is in the form of matrices, and matrix multiplication does not change the dimensions of the matrices, thus solving the dimensional explosion problem caused by multiplying ciphertext vectors in previous schemes without needing a key exchange process to reduce the dimensions of the ciphertext.
④ Floating Point Fully Homomorphic Encryption Scheme – CKKS Scheme
The CKKS (Cheon-Kim-Kim-Song) scheme, proposed in 2017, is a new scheme that supports additive and multiplicative homomorphic operations on floating-point numbers for real or complex numbers, with the resulting calculations being approximate values, suitable for scenarios such as training machine learning models where precise results are not required. Due to the necessity of floating-point homomorphic operations in specific scenarios, both HElib and SEAL open-source libraries support the CKKS scheme.
Open-source tools for fully homomorphic engineering implementation:
-
HElib
-
SEAL
Currently, fully homomorphic encryption algorithms are still in a development stage primarily focused on academic research, and existing schemes face unavoidable performance issues such as high computational and storage overhead, making it challenging to bridge the gap to efficient engineering applications, while also facing the lack of relevant international and domestic standards. Therefore, when attempting to implement homomorphic encryption applications, it may be advisable to utilize more mature and better-performing partially homomorphic encryption algorithms such as the Paillier additive homomorphic encryption algorithm to address application scenarios that only require additive or scalar multiplication homomorphic operations, or to approximate fully homomorphic scenarios by transforming complex computational needs into forms that only require additive or scalar multiplication operations.
References
[1] Rivest R L, Adleman L, Dertouzos M L. On data banks and privacy homomorphisms[J]. Foundations of secure computation, 1978, 4(11): 169-180.
[2] Rivest R L, Shamir A, Adleman L. A method for obtaining digital signatures and public-key cryptosystems[J]. Communications of the ACM, 1978, 21(2): 120-126.
[3] ElGamal T. A public key cryptosystem and a signature scheme based on discrete logarithms[J]. IEEE transactions on information theory, 1985, 31(4): 469-472.
[4] Paillier P. Public-key cryptosystems based on composite degree residuosity classes[C]//International conference on the theory and applications of cryptographic techniques. Springer, Berlin, Heidelberg, 1999: 223-238.
[5] Boneh D, Goh E J, Nissim K. Evaluating 2-DNF formulas on ciphertexts[C]//Theory of Cryptography Conference. Springer, Berlin, Heidelberg, 2005: 325-341.
[6] Gentry C. Fully homomorphic encryption using ideal lattices[C]//Proceedings of the forty-first annual ACM symposium on Theory of computing. 2009: 169-178.
[7] Gentry C, Halevi S. Implementing Gentry’s fully-homomorphic encryption scheme[C]//Annual international conference on the theory and applications of cryptographic techniques. Springer, Berlin, Heidelberg, 2011: 129-148.
[8] Brakerski Z, Gentry C, Vaikuntanathan V. (Leveled) fully homomorphic encryption without bootstrapping[J]. ACM Transactions on Computation Theory (TOCT), 2014, 6(3): 1-36.
[9] Brakerski Z. Fully homomorphic encryption without modulus switching from classical GapSVP[C]//Annual Cryptology Conference. Springer, Berlin, Heidelberg, 2012: 868-886.
[10] Fan J, Vercauteren F. Somewhat Practical Fully Homomorphic Encryption[J]. IACR Cryptology ePrint Archive, 2012, 2012: 144.
[11] Gentry C, Sahai A, Waters B. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based[C]//Annual Cryptology Conference. Springer, Berlin, Heidelberg, 2013: 75-92.
[12] Cheon J H, Kim A, Kim M, et al. Homomorphic encryption for arithmetic of approximate numbers[C]//International Conference on the Theory and Application of Cryptology and Information Security. Springer, Cham, 2017: 409-437.
[13] Smart N P, Vercauteren F. Fully homomorphic SIMD operations[J]. Designs, codes and cryptography, 2014, 71(1): 57-81.
[14] Gentry C, Halevi S, Smart N P. Homomorphic evaluation of the AES circuit[C]//Annual Cryptology Conference. Springer, Berlin, Heidelberg, 2012: 850-867.