5Typical Symmetric Encryption Algorithms
This article introduces AES, SM4, and ZUC as representatives. AES, the Advanced Encryption Standard, is a block cipher algorithm adopted by the United States federal government; SM4 is a commercial block cipher algorithm developed and promoted for use in China; ZUC, the Zu Chongzhi algorithm, is a stream cipher algorithm independently developed in China and was approved as the international standard for 4G in 2011.
5.1 AES
On April 15, 1997, the U.S. ANSI initiated the AES (Advanced Encryption Standard) solicitation, which underwent three candidate meetings, and on October 2, 2000, NIST announced the Rijndael algorithm as AES. Rijndael was designed by Belgian Joan Daemen and Vincent Rijmen, and its prototype is the Square algorithm.
The Rijndael algorithm uses an SPN structure, with both block length and key length being variable, independently specified as 128 bits, 192 bits, or 256 bits. Unlike AES, the plaintext block length is fixed at 128 bits, while the key length can be 128 bits, 192 bits, or 256 bits. Therefore, based on the key length, AES is divided into AES-128 (10 rounds), AES-192 (12 rounds), and AES-256 (14 rounds).
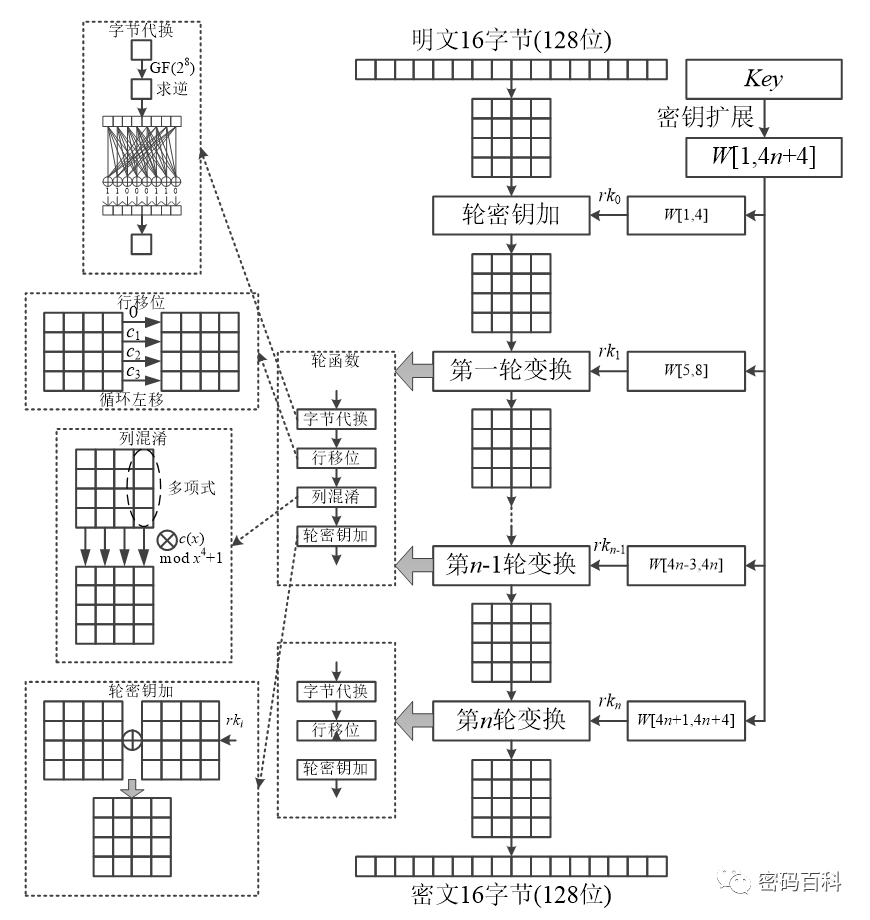
Figure 10 AES Algorithm Structure
The AES algorithm structure utilizes four transformations: byte substitution, row shifting, column mixing, and round key addition. The byte substitution operates independently on each byte, as shown in the byte substitution step in Figure 10, which can be viewed as an S-box replacement, and the S-box is reversible; row shifting and column mixing are common methods in block ciphers, where the process of cyclic shifting of each row is reversible, and in column mixing, polynomials from GF(2^8) are used for multiplication, ensuring that the multiplication is reversible; the round key addition is the process of XORing with the round key, which is also reversible. Thus, the decryption process of AES is the inverse of the encryption process, where each transformation uses its inverse transformation. The key expansion of AES is determined by the key length, with each round key generated being a fixed length of 128 bits, and the number of round keys generated equals the number of iterations plus one; the key expansion process is not reflected in Figure 10, and interested readers can refer to related literature.
The design of AES uses knowledge related to finite fields GF(2^8), ensuring the overall reversibility of the algorithm. For those interested in the mathematical foundation and design concepts of the Rijndael algorithm, please refer to the relevant literature.
5.2 SM4
The SM4 (originally named SMS4) algorithm is a block cipher algorithm used for the WAPI (Wireless LAN Authentication and Privacy Infrastructure) wireless LAN authentication and confidentiality framework. It was published by the National Cryptography Administration in 2006 as the first commercial cryptographic algorithm in China. On March 21, 2012, the National Cryptography Administration released GM/T0002-2012 “SM4 Block Cipher Algorithm,” establishing it as a standard in the cryptography industry. In August 2016, GB/T 32907-2016 “Information Security Technology SM4 Block Cipher Algorithm” was released, becoming a national standard. This algorithm uses a generalized non-balanced Feistel structure, with both block length and key length set to 128 bits. Both the encryption algorithm and the key expansion algorithm utilize a 32-round nonlinear iterative structure, where the data decryption and encryption algorithms have the same structure, differing only in the order of round key usage, with the decryption round keys being the inverse order of the encryption round keys.
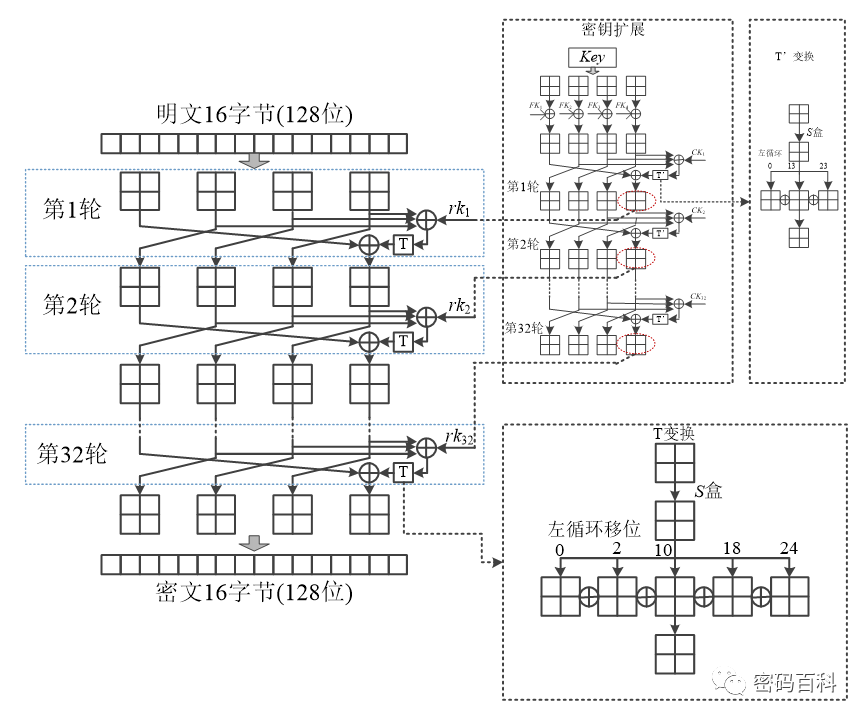
Figure 11 SM4 Algorithm Structure
The SM4 algorithm is constructed based on a regular permutation, with each round of transformation constituting a regular permutation. Its cryptographic properties are that under different keys, the results of the round transformations must be different; the output must also differ under the same plaintext input with different keys. Each round transformation in the algorithm combines the roles of “confusion” and “diffusion.” Each round only alters 1/4 of the data, resulting in a weaker diffusion effect per round; however, with a total of 32 rounds, it ensures that data changes occur overall eight times. The key expansion and encryption processes of the algorithm are similar, also using a 32-round iterative method to generate round keys, differing only in the left cyclic shifts in the T transformation and T’ transformation.
Since the encryption structure of SM4 and the structure of key expansion are very similar, it raises the idea that if the T’ transformation in the key expansion process directly uses the T transformation from the encryption process, the overall algorithm would turn into two identical 32-round encryption operations. The first 32-round encryption operation encrypts the 128-bit key using the fixed round key CKi, saving the fourth part of length 32 bits as rki for each round; the second 32-round encryption operation encrypts the 128-bit plaintext using the round key rki, ultimately producing the ciphertext. This approach can reduce resource usage in implementation, but whether it affects security remains to be studied.
5.3 ZUC
The ZUC algorithm (Zu Chongzhi algorithm) is named after the ancient Chinese mathematician Zu Chongzhi and was developed by the National Key Laboratory of Information Security and other institutions. In September 2011, it was approved as the international standard for the new generation of broadband wireless mobile communication systems (LTE), namely the international standard for 4G. The ZUC algorithm is the first cryptographic algorithm from China to become an international standard. The algorithm generates a key stream oriented to words using a block cipher approach, with the input being a 128-bit initial key and a 128-bit initial vector (IV), and the output is a key stream in units of 32-bit words (referred to as key words). The algorithm is logically divided into three layers: upper, middle, and lower. The upper layer consists of 16 levels of linear feedback shift registers (LFSRs), the middle layer is for bit reorganization, and the lower layer is a nonlinear function F. Figure 12 illustrates the structure of the ZUC algorithm.
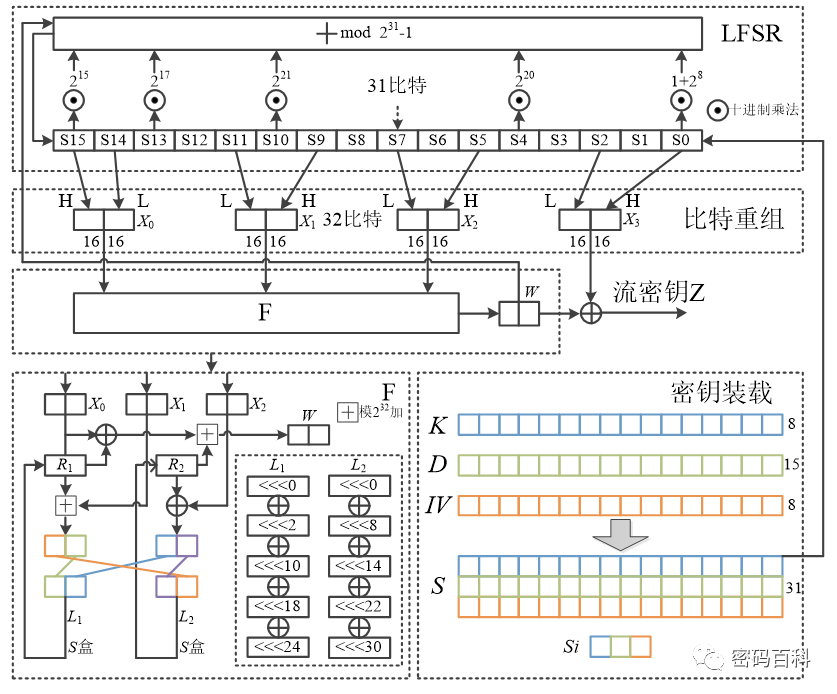
Figure 12 ZUC Algorithm Structure
The operation of the ZUC algorithm is divided into two phases: the initialization phase and the working phase. The initialization phase loads the key into the LFSR, sets R1 and R2 in F to all zeros, and performs the sequence of “bit reorganization -> F -> LFSR” 32 times. After the initialization phase is completed, it enters the working phase. First, it performs one “bit reorganization -> F -> LFSR,” discarding the output W from F; then it enters the stream key output phase, executing “bit reorganization -> F -> LFSR” in sequence, outputting a 32-bit key word Z for each cycle.
The output of the ZUC algorithm’s LFSR is an m-sequence over the finite field GF(2^31-1), which has good randomness, providing a well-randomized drive for the middle layer’s bit reorganization.
6.Applications of Symmetric Encryption Algorithms
The advantage of symmetric encryption technology lies in its high computational efficiency and low system overhead, making it suitable for the encryption of large amounts of data transmission. Block cipher algorithms are commonly used in network communication; generally, our message data is encrypted and transmitted using block cipher algorithms. Stream ciphers are applied in scenarios such as video encryption and voice encryption. In practical use, block cipher algorithms do not simply encrypt plaintext data according to the block length sequentially; when the block length is insufficient, padding is required, and various working modes are applied based on actual needs. Stream ciphers adhere to the “one-time pad” characteristic, do not differentiate between working modes, and process data in real-time, making them more suitable for hardware implementation.
6.1 Padding Modes for Block Algorithms
The length of the data to be encrypted will not always be an exact multiple of the block length. Therefore, when invoking the block algorithm for encryption, the last group of plaintext must be padded to the entire block length, and during decryption, the padded bytes can simply be removed. Common padding methods include ANSI X.923, PKCS#7, zero padding, ISO/IEC 7816-4, ISO 10126, etc.
6.2 Working Modes of Block Algorithms
The working modes of block algorithms include ECB, CBC, CFB, OFB, CTR, XTS, HCTR, BC, and OFBNLF. The first four are the main working modes, while the latter five are briefly introduced. Among the first four, the most commonly used are ECB and CBC modes.
6.2.1 ECBWorking Mode
The Electronic Code Book (ECB) is the earliest and simplest mode. It divides the data to be encrypted into several groups, each of the same size as the algorithm’s block length, and then encrypts each group using the same key.Advantages:Simple, conducive to parallel computation, and errors are not transmitted.Disadvantages:Cannot hide the plaintext pattern, and is vulnerable to active attacks. Therefore, this mode is suitable for encrypting small messages.
6.2.2 CBCWorking Mode
The Cipher Block Chaining (CBC) mode divides the data to be encrypted into l groups, each of length n, where the first group of data is XORed with the initial vector (IV) before encryption. Then, before encrypting each group of data, it is XORed with the previous ciphertext group before encryption, as shown in Figure 13.Advantages:Not easily susceptible to active attacks, more secure than ECB, suitable for transmitting long messages, such as traffic data for SSL VPN and IPSec VPN.Disadvantages:Not conducive to parallel computation, and there is error propagation.
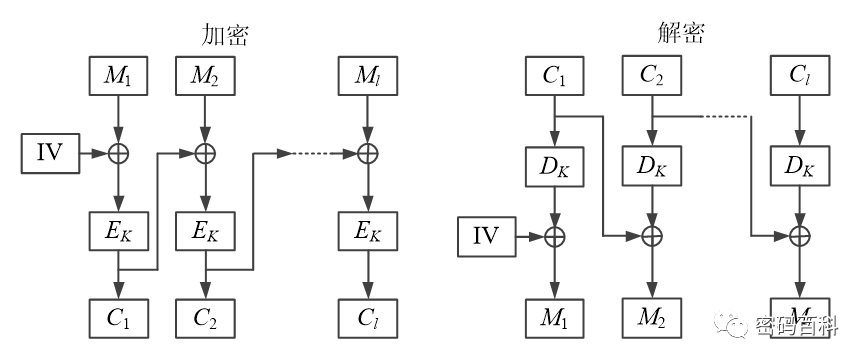
Figure 13 CBC Working Mode
6.2.3 CFB Working Mode
The Cipher Feedback (CFB) mode divides the data to be encrypted into l groups, each of length n, where the block length of the block cipher is N, and n ≤ N. The feedback buffer FB has a length of r (N ≤ r ≤ 2N), and is initialized with the initial vector IV (length r). The first N bits are selected from FB, which are encrypted using the block cipher algorithm, and the first n bits of the encryption result are XORed with the plaintext to obtain the ciphertext. The ciphertext is placed at the end of the feedback buffer FB, and the first n bits are discarded. The operation is repeated to obtain the ciphertext for the next plaintext group, as shown in Figure 14.Advantages:Hides the plaintext pattern, transforming the block cipher into a stream cipher, allowing real-time encryption of data smaller than the block size.Disadvantages:Not conducive to parallel computation, and there is error propagation.
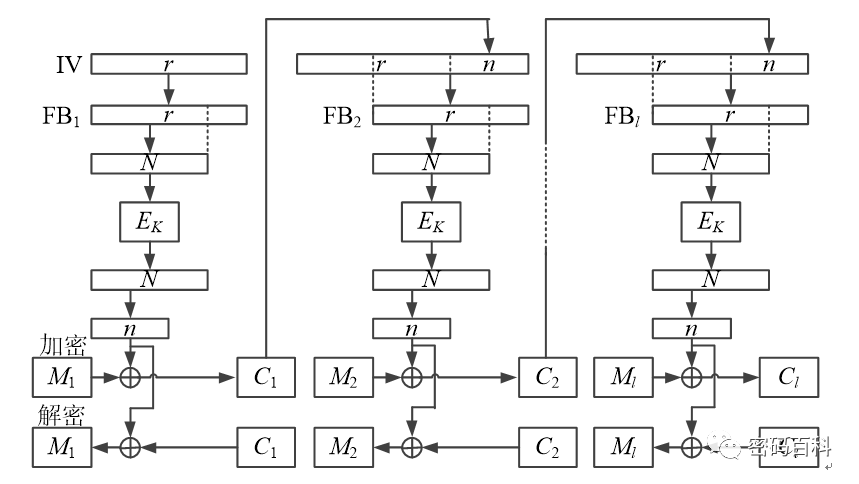
Figure 14 CFB Working Mode
6.2.4 OFB Working Mode
The Output Feedback (OFB) mode is similar to the CFB mode but does not have a feedback buffer. The data to be encrypted is divided into l groups, each of length n, where the block length of the block cipher is N, and n ≤ N. The initial vector IV is the same length as the block cipher’s block length. Figure 15 illustrates the process of the OFB mode.Advantages:Hides the plaintext pattern, transforming the block cipher into a stream cipher, allowing real-time encryption of data smaller than the block size.Disadvantages:Not conducive to parallel computation, and active attacks on the plaintext are possible, with error propagation.
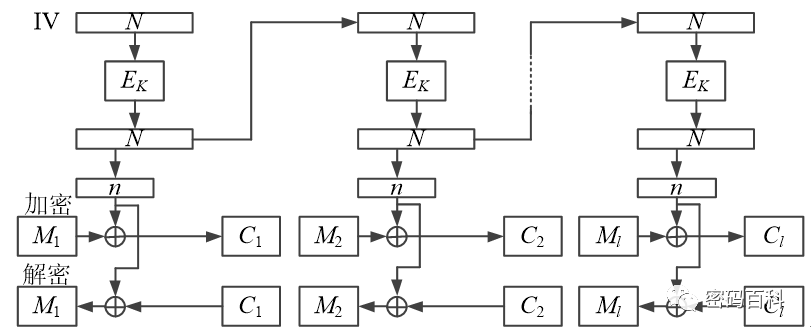
Figure 15 OFB Working Mode
6.2.5 CTR Working Mode
The Counter (CTR) mode divides the data to be encrypted into l groups, except for the last group, where each group is the same length as the block cipher’s block length n. The last group has a length d ≤ n. The encryption and decryption parties agree on a sequence of counting numbers T1, T2, …, Tl, each of length n, and use the algorithm to encrypt the counting sequence. The encryption result is XORed with the plaintext to obtain the ciphertext, as illustrated in Figure 16.
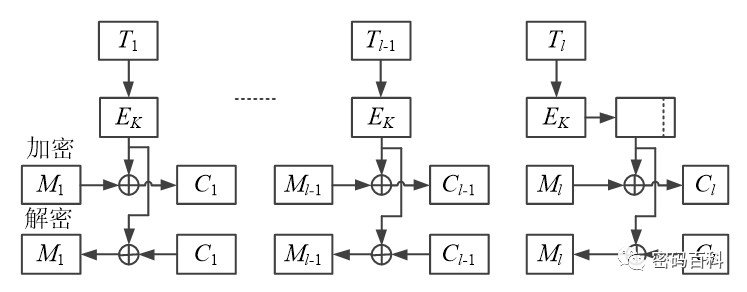
Figure 16 CTR Working Mode
6.2.6 XTS Working Mode
The XEX tweakable block cipher with ciphertext stealing (XTS) divides the data to be encrypted into l groups, except for the last group, where each group is the same length as the block cipher’s block length n. The last group has a length d ≤ n, and the tweak TW has a length of n, with two keys K1 and K2 for the block cipher algorithm. In the CTR working mode, the operation involving α is a multiplication in a finite field, as shown in Figure 17. When the last group length matches the block cipher’s block length n, the last two groups in the figure are not swapped.
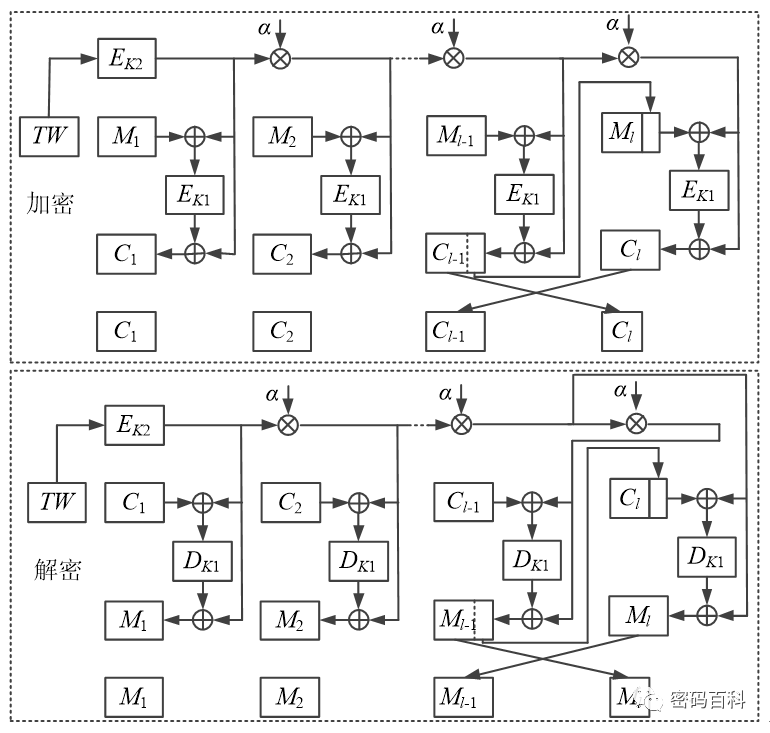
Figure 17 XTS Working Mode
6.2.7 HCTR Working Mode
The Universal hash function based CTR (HCTR) divides the data to be encrypted into l groups, except for the last group, where each group is the same length as the block cipher’s block length n. The last group has a length d ≤ n, and the tweak TW has a length of n, with two keys K1 and K2, where K1 is the key for the block cipher algorithm and K2 has a length of n. In the HCTR working mode, a keyed universal hash function HK(·) is used, and the specific encryption process is shown in Figure 18. The decryption process is the same as the encryption process, where the ciphertext C and plaintext M are swapped, and the encryption process EK1 is replaced with the decryption process DK1.
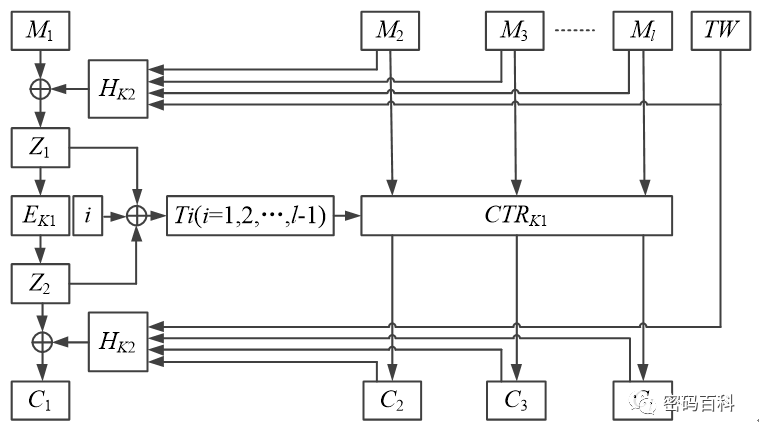
Figure 18 HCTR Working Mode
6.2.8 BC Working Mode
The Blockchaining (BC) mode divides the data to be encrypted into l groups, each of the same length as the block cipher’s block length n, with key K and initial vector IV, as shown in Figure 19.
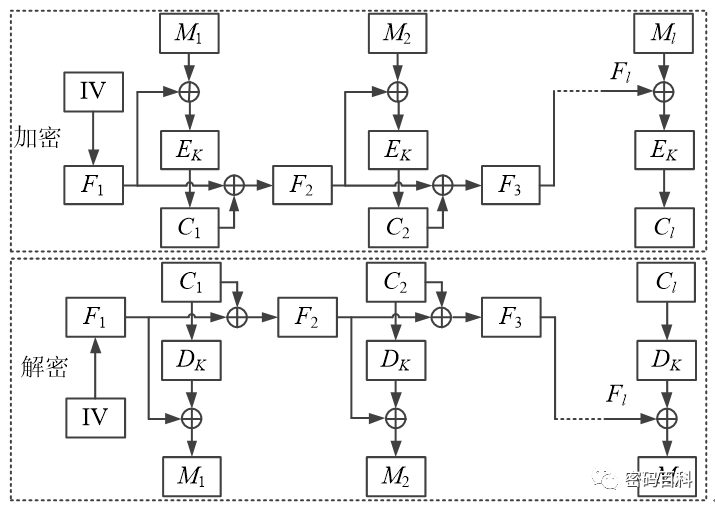
Figure 19 BC Working Mode
6.2.9 OFBNLF Working Mode
The Output Feedback with a Nonlinear Function (OFBNLF) working mode divides the data to be encrypted into l groups, each of the same length as the block cipher’s block length n, with key K and initial vector IV, as shown in Figure 20.
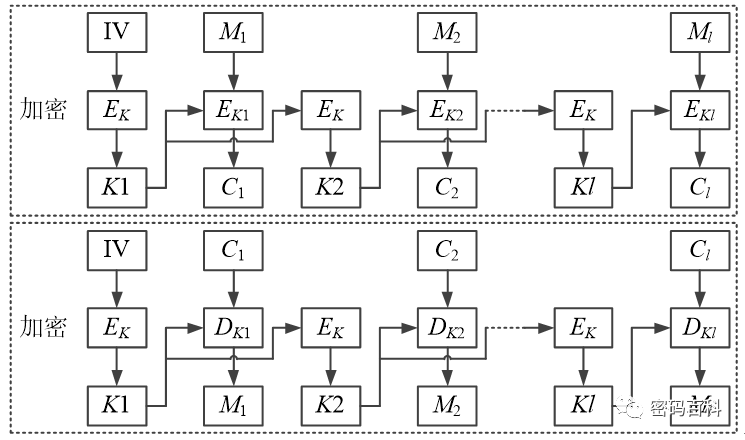
Figure 20 OFBNLF Working Mode
6.3 Application Areas of Symmetric Algorithms
In China, the “Cryptography Law” classifies cryptography into core cryptography, ordinary cryptography, and commercial cryptography. Core and ordinary cryptography are used to protect state secret information, with core cryptography safeguarding information at the highest level of confidentiality, while ordinary cryptography protects information at the confidential level. Commercial cryptography is used to protect information that does not belong to national secrets; thus, commercial cryptography is what people encounter most in daily life.
In commercial cryptography, block ciphers include SM1, SM4, and SM7, while stream ciphers include ZUC. The SM1 algorithm has a block length and key length of 128 bits, and its security and hardware implementation performance are comparable to AES. The SM1 algorithm is currently not publicly disclosed and exists in the form of an IP core within chips, used for the development of chips, smart IC cards, smart cryptographic keys, POS, ATMs, PCI cryptographic cards, server cryptographic machines, and IPSec VPN products. The SM4 algorithm is public, and its structure has been introduced earlier; it can be implemented in both software and hardware. In hardware products, most products will use both SM1 and SM4 algorithms, generally using SM1 for encrypting short data and SM4 for encrypting long data. The SM7 algorithm is also currently not publicly disclosed, with a block length and key length of 128 bits, used in the development of non-contact ICs and access control systems, applicable to resource-constrained devices such as community access cards, chip-enabled tickets, and campus cards. The ZUC stream cipher is the international standard cryptographic algorithm used in mobile communication 4G networks, and it is also utilized in commercial cryptographic products, particularly in server cryptographic machines for encrypting the transmission of video, voice, and other streaming data.
Cryptographic algorithms are closely related to our lives. Although we may not perceive their presence, every time we swipe a card for payment or send a message, there are numerous cryptographic computations behind them, protecting our information security through these complex and invisible algorithms.
Note: Authorized Reprint from Shenzhen Cryptography.
Follow/Subscribe Us

