The colorful world is exceptionally complex, and it is difficult for us to understand its mysteries. Although humans are arrogant, claiming to have conquered Mount Everest after climbing it once, or to have conquered the Moon after visiting it once, we clearly understand that we have only taken a step into these realms, and we are far from grasping even a tiny bit of information about Everest and the Moon.
The world is so complex, and we are so insignificant that we dare not claim to have mastered the laws of the world’s operation.
In the realms of physics and chemistry, we have undergone a long exploration and gradually mastered some simple laws. For example, we have understood the law of conservation of momentum, the first, second, and third laws of thermodynamics, and the properties of polymer materials, among others. Nevertheless, there are still many unsolved mysteries in nature that challenge the wisdom and exploratory spirit of scientists. For instance, dark matter and dark energy are believed to be the main components of the universe, yet their essence and properties remain a mystery. Due to the complexity of dark matter and dark energy, scientists have discovered through certain observations and numerous simulations that approximately 27% of the universe is dark matter and 68% is dark energy, while the ordinary matter we are familiar with only accounts for 5% of the universe. However, the specific composition and mechanisms of dark matter and dark energy are still unknown. Another example is the accelerating expansion of the universe, which puzzles scientists. Some believe that gravity should slow down the expansion of the universe, but observational data indicates that the expansion rate is increasing. Scientists have proposed dark energy as a possible explanation, but many mysteries remain regarding the nature and mechanisms of dark energy. In the field of biochemistry, the origin of life is a significant question. Although scientists have proposed some theories and hypotheses, many mysteries remain about how life evolved from inorganic matter. The origin of life involves complex chemical reactions, self-assembly processes, and the origin of genetic information, and these issues are far from fully resolved. Consciousness and thought are at the core of human cognition, yet their essence and origin remain a mystery. Despite some progress in neuroscience and cognitive science, our understanding of how consciousness and thought arise and their relationship with the brain is still limited. Time and space are fundamental concepts in physics, yet their essence and origin still pose many unsolved mysteries. For example, whether the passage of time is absolute or relative, and how the curvature and topological structure of space affect the behavior of matter and energy are focal points of debate in the scientific community.
However, compared to nature, the complexity of the human world is even greater. In terms of complexity, the complexity of nature usually manifests at different scales. On a cosmic scale, we can observe vast and complex structures such as galaxies, planets, and stars. However, at smaller scales, such as molecules, atoms, and fundamental particles, the laws of nature become simpler and more predictable. In contrast, the human world involves more social, economic, political, and cultural factors, and the interactions of these factors make the human world more complex. Regarding the regularity and predictability of things, we know that there are many fundamental physical and biological laws in nature that can be described and explained using concise mathematical formulas or theories. For example, the law of universal gravitation, the laws of light propagation, and the theory of biological evolution all play a universal role in nature and have a high degree of predictability. In contrast, the human world involves more human behaviors and decisions, which are influenced by individual subjective will, cultural background, social relationships, and other factors, making them more difficult to predict and describe accurately. From a research methodology perspective, when we explore the operational characteristics and laws of the human world, we need to build models. Since the laws of nature are relatively simple and predictable, scientists can use simplified mathematical models to describe and explain natural phenomena. These models are usually based on some basic assumptions and rules and can be verified through experiments and observations. In contrast, modeling the human world is more challenging because it involves more variables and uncertainties. Human behavior is often influenced by complex factors such as emotions, morals, and culture, which are difficult to capture and predict using simple mathematical models. In summary, although there are also complex phenomena in nature, such as climate systems and ecosystems, overall, the phenomena in nature are simpler compared to the human world. This does not mean that the complexity of nature is not worth studying; on the contrary, it is precisely the complexity of nature that stimulates scientists’ curiosity and research motivation. Through the study of nature, we can deepen our understanding of natural laws and apply this knowledge to solve complex problems in the human world.
As mentioned earlier, due to the reasons of complexity, scientists exploring the world need to construct some simple models for the things they need to study, first obtaining some basic characteristics and laws, and then gradually adding specific variables to these models for a particular problem, ultimately allowing for specific research on these events. This deductive approach from general to specific is often adopted by some scientists. There are also studies that explore the unknown, first observing a specific event to obtain some basic characteristics and evolutionary processes of the specific thing, and then performing the same operation on another similar event. As events accumulate to a certain extent, the evolutionary process and characteristics of different events can be summarized to form basic characteristics and laws. Based on this, for this type of event, corresponding models can be constructed according to existing knowledge, and the models can be adjusted to fit the actual situation, resulting in a basic model. Then, following the above method, we can explore this world more deeply.
Whether it is deductive → inductive or inductive → deductive → inductive, model analysis plays a significant role in scientific exploration. The closer a model is to reality, the greater its computational complexity. Moreover, due to the limitations of analytical methods, some models are difficult to find their analytical solutions. This poses significant challenges for scientific research. As mentioned earlier, to more accurately describe phenomena in the real world, the models constructed by scientists often become more complex. This complexity can manifest in the structure of the model, the number of parameters, and the complexity of the equations. The closer a model is to reality, the more factors and variables it needs to consider, leading to increased computational complexity. Some complex models are difficult to find analytical solutions, meaning they cannot be expressed with simple mathematical formulas. This is because complex models often involve nonlinear, multivariable, and coupled equations that are challenging to solve directly. For these models, scientists typically need to use numerical methods or approximation methods for computation and analysis, which increases the difficulty of model analysis. Additionally, scientists use various analytical methods to study models, such as mathematical derivation, computational simulation, and experimental validation. However, these analytical methods are not without flaws. Mathematical derivation may be limited by the complexity of the equations, computational simulations may be constrained by computational resources and algorithms, and experimental validation may be limited by technology and resources. These flaws can lead to incompleteness and uncertainty in model analysis.
When it comes to complex physical, chemical, or biological systems, it is often challenging to find analytical solutions. For example, in quantum mechanics, the Schrödinger equation that describes the behavior of atoms and molecules is a complex partial differential equation. For multi-electron systems or systems with complex interactions, it is difficult to find analytical solutions to the Schrödinger equation. Therefore, scientists typically use numerical methods, such as quantum chemistry calculations, to approximate solutions to these equations. Similarly, fluid dynamics models are used to describe the motion and interaction of fluids. For complex fluid systems, such as turbulence, multiphase flow, or non-Newtonian fluids, the relevant equations become very complex. These equations often contain nonlinear and coupled terms, making them difficult to solve using analytical methods. Therefore, scientists use computational fluid dynamics methods, such as numerical simulations and computer simulations, to study these complex fluid systems. Taking ecosystems as another example, ecosystems involve dynamic changes in interactions between multiple species and ecological processes. To describe the behavior of ecosystems, scientists have constructed complex ecological models, such as food web models and population dynamics models. These models typically contain a large number of differential equations and parameters, making it difficult to find analytical solutions. Therefore, scientists use numerical simulations and computational methods to simulate and analyze the behavior of ecosystems. In recent years, neural network models have played a significant role in data modeling, and further, neural network models are used to simulate and understand the functions and behaviors of the brain. As the complexity of neural network models increases, involving numerous interactions between neurons and synapses, analytical solutions become very difficult. Therefore, scientists use computational methods, such as Monte Carlo simulations and numerical simulations, to study and analyze the behavior of neural networks. In these examples, complex models often involve nonlinear, multivariable, and coupled equations that are difficult to solve using analytical methods. Therefore, scientists turn to numerical methods and computational methods to approximate solutions to these models to better understand and explain phenomena.
Taking the previously discussed examples to illustrate the complexity of this issue, for instance, the general expression of the Schrödinger equation is: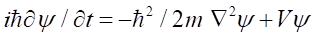
. ħ is the reduced form of Planck’s constant (ħ=h/2π, where h is Planck’s constant), ψ is the wave function, t is time, m is the mass of the particle, ∇² is the Laplacian operator, and V is the potential energy function. The Schrödinger equation can be divided into the time-independent stationary Schrödinger equation and the time-dependent non-stationary Schrödinger equation. The time-independent stationary Schrödinger equation is:
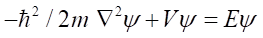, in which E is the energy of the particle; the time-dependent non-stationary Schrödinger equation is: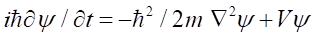, which describes the behavior of the wave function over time. The Schrödinger equation is a partial differential equation in which the wave function ψ is a complex function. It describes the evolution and behavior of quantum systems, including information about the position, momentum, and energy of particles. By solving the Schrödinger equation, one can obtain the wave function of a particle, thereby gaining information about the probability distribution and physical properties of the particle. The analytical solution of the time-dependent non-stationary Schrödinger equation remains a significant challenge. Another example is the population dynamics model, which is a very complex model. Its mathematical model is as follows:
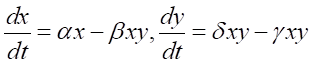. x and y represent the number of prey and predators, respectively, and xy represents the interaction situation, while α, β, δ, and γ represent parameters. The solution of this model is also very challenging.
As mentioned earlier, the complexity of problems in social systems far exceeds that of problems in nature. To truly describe various behaviors in human society, one generally adopts systems of PDE equations, which are more difficult to analyze than the aforementioned models, thus requiring methods to solve such problems.
Although analytical solutions may be difficult to obtain, numerical methods and computational methods provide powerful tools for scientists to explore and study the behavior of complex systems. However, while numerical analysis methods are relatively convenient, they generally assume that a certain variable meets specific conditions to explore the characteristics and evolutionary processes of events. In reality, these assumptions are often dynamic variables that change constantly, leading to certain flaws in numerical solutions. Nevertheless, this remains a method of scientific exploration.
Multi-Agent modeling is a method for modeling complex behaviors in complex systems. Through computer languages, it describes very complex behaviors, including intricate processes.Multi-Agent models are designed to describe the interactions and behaviors of multiple agents. These agents can be robots, individuals, organizations, or other entities with decision-making capabilities. Due to the interactions and complexities among agents, the solutions to Multi-Agent models are typically obtained through numerical methods. In a Multi-Agent model, each agent makes decisions and takes actions based on its internal state, perceived information, and interactions with other agents. This interaction can lead to global behaviors and evolution of the system. To understand and predict these behaviors, the model needs to be solved. Since Multi-Agent models often involve a large number of agents and complex interaction networks, it is challenging to solve the model using analytical methods. Analytical methods typically rely on precise mathematical derivations and solving techniques, suitable for simple systems or models with simplified assumptions. However, in Multi-Agent models, the interactions and decisions among agents are often nonlinear, making it impossible to obtain precise solutions through analytical methods. Therefore, using numerical methods to solve Multi-Agent models is a common practice. Numerical methods discretize time and space and use numerical approximation techniques to transform the model into a form that can be computed on a computer. Common numerical methods include iterative methods, numerical optimization, Monte Carlo simulations, and agent-based reinforcement learning. Solving Multi-Agent models using numerical methods can provide approximate results about system behavior and evolution. These results can be used to analyze and predict the decisions, interactions, and overall properties of agents. Although numerical solutions have approximation errors, they provide valuable tools for studying and understanding the behavior of complex systems. The difficulty of this Multi-Agent modeling is not very high; since Multi-Agent models involve complex interactions and decision-making processes among agents, numerical methods are typically required to solve them. Numerical solutions provide approximate results for system behavior and evolution, offering important tools for studying and analyzing Multi-Agent systems. Moreover, with the help of computer technology, solving these models is relatively convenient. We can obtain numerical solutions for various specific situations, which we refer to as simulating various scenarios.
Taking the aforementioned population dynamics model as the main focus, we assume a wolf-sheep-grass model, where, according to common sense, wolves eat sheep, sheep eat grass, wolves and sheep can reproduce, and grass can regrow. Based on the analysis methods of Multi-Agent models, we constructed a model and assumed various situations, determining the changes in the populations of these three groups under different scenarios. If there are initially 140 sheep and 10 wolves, with each movement consuming 0.8 energy, the grass growth rate is 0.3, the energy obtained by sheep from a unit of grass is 1.2, and the energy obtained by wolves from a single sheep is 4.1, the changes in the three species would be:
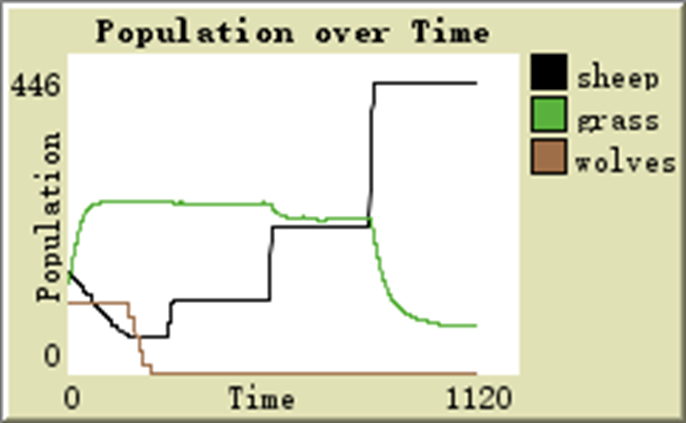
In the same situation, if the energy consumed per unit movement is 1.8 and the grass growth rate is 0.1, the changes would present as follows:
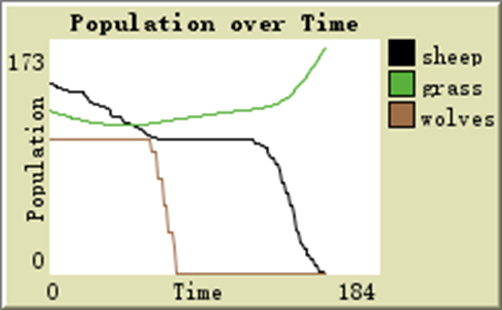
From these two specific scenarios, the evolution presents complex diversity. This numerical solution makes the study of a specific event more convenient.
Due to the greater complexity of human society, the research is more challenging. We know that the prisoner’s dilemma is a very famous game model that describes the complex situation when both parties engage in transactions: if one party chooses to cooperate while the other does not, the outcome will be seized by the non-cooperating party; if both choose to cooperate, they will share the benefits of the outcome; if both choose not to cooperate, both will suffer losses but will gain slightly more than the one who chose to cooperate in the first scenario. If there are only two players, the problem is much simpler, but now assume that there are many people in the system, and assume that there are several types of people with the following attributes: random decision-makers, who choose to cooperate or not based on a specific probability; steadfast cooperators, who always choose to cooperate when trading; steadfast non-cooperators, who choose never to cooperate with others; tit-for-tat types, who cooperate if the other party cooperates, otherwise they do not cooperate next time; unforgiving types, who never cooperate again if the other party does not cooperate; and unknown types, who do not know what strategy to choose. The complexity of this problem is evident, and it is challenging to obtain accurate answers using current analytical methods. Therefore, we establish a Multi-Agent model, which yields the following results. Assuming that the number of each type of person is equal, set to 10, the average earnings of each type are as follows:
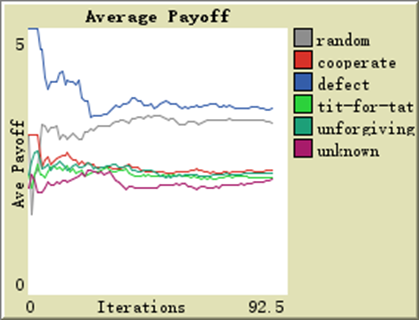
At this point, the non-cooperating type will have better earnings, followed by the random type, cooperating type, and unforgiving type. However, the random type’s initial earnings are not the second highest; instead, they decrease initially and then increase as interactions progress. If we eliminate steadfast non-cooperators while keeping other conditions unchanged, the earnings of each type will become:
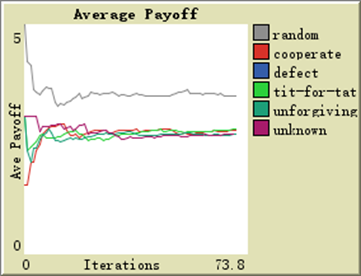
At this point, without steadfast non-cooperators, the random type has the best earnings, but compared to the first scenario, a strange phenomenon is observed: the earnings of the random type gradually decline rather than following the initial decrease and subsequent increase seen in the first scenario. This intriguing phenomenon will undoubtedly prompt further analysis. We will not demonstrate more scenarios; overall, this complexity far exceeds our imagination, and analytical methods cannot account for it. Using the Multi-Agent model simplifies complex analyses.
Nevertheless, we can see that the Multi-Agent model plays a crucial role in analyzing different scenarios under specific models, but it is challenging to explain the principles behind some singular phenomena. In such cases, by determining certain constraint variables as constants, we can use analytical methods to solve for the core reasons, which is of great significance for understanding phenomena. Furthermore, the analysis of Multi-Agent models, when scenarios are at critical states, yields results that vary widely and do not conform to any statistical laws. Problems in these critical situations require critical research methods.
This article presents a preliminary view on this issue, hoping to achieve a stimulating effect through this article. I apologize for any shortcomings in the text!