If you ask me, which algorithm is the most important? I might answer “Public Key Encryption Algorithm“.

Because it is the cornerstone of computer communication security, ensuring that encrypted data cannot be cracked. You can imagine the consequences if credit card transactions are compromised.

Before getting into the main topic, let me briefly introduce what a “public key encryption algorithm” is.

01

A Bit of History

Before 1976, all encryption methods followed the same pattern:

(1) Party A chooses a certain encryption rule to encrypt the information;

(2) Party B uses the same rule to decrypt the information.

Since the same rule (referred to as “key”) is used for both encryption and decryption, this is known as “Symmetric Key Algorithm“.

This encryption method has a major weakness: Party A must tell Party B the encryption rule; otherwise, decryption is impossible. Storing and transmitting the key becomes the most troublesome issue.

In 1976, two American computer scientists, Whitfield Diffie and Martin Hellman, proposed a groundbreaking idea that allows decryption to be completed without directly transmitting the key.

This is known as “Diffie-Hellman Key Exchange Algorithm“. This algorithm inspired other scientists. People realized that encryption and decryption could use different rules, as long as there is some correspondence between the two rules, thus avoiding direct key transmission.

This new encryption model is called “Asymmetric Key Algorithm“.

(1) Party B generates two keys (public key and private key). The public key is public, anyone can obtain it, while the private key is kept secret.

(2) Party A obtains Party B’s public key and uses it to encrypt the information.

(3) Party B receives the encrypted information and decrypts it using the private key.

If the information encrypted with the public key can only be decrypted with the private key, then as long as the private key is not leaked, the communication is secure.

In 1977, three mathematicians, Rivest, Shamir, and Adleman designed an algorithm that can achieve asymmetric encryption. This algorithm is named after the three of them, known as the RSA Algorithm. Since then, the RSA algorithm has been the most widely used “asymmetric encryption algorithm”. It is no exaggeration to say that wherever there are computer networks, there is the RSA algorithm.

This algorithm is very reliable; the longer the key, the harder it is to crack. According to disclosed literature, the longest RSA key that has been cracked is 768 bits. That is, keys longer than 768 bits have not been cracked (at least no one has publicly announced it). Therefore, it can be considered that a 1024-bit RSA key is basically secure, and a 2048-bit key is extremely secure.

Now, I will get to the main topic and explain the principles of the RSA algorithm. This article is divided into two parts, and today is the first part, introducing four mathematical concepts that will be used. You can see that the RSA algorithm is not difficult; it only requires a bit of number theory knowledge to understand.

02

Coprime Relationship

If two positive integers have no common factors other than 1, we say that these two numbers are coprime. For example, 15 and 32 have no common factors, so they are coprime. This means that non-prime numbers can also form a coprime relationship.

Regarding the coprime relationship, the following conclusions can be easily drawn:

1. Any two prime numbers are coprime, for example, 13 and 61.

2. If one number is prime and the other is not a multiple of the former, then they are coprime, for example, 3 and 10.

3. If the larger of two numbers is prime, then they are coprime, for example, 97 and 57.

4. 1 and any natural number are coprime, for example, 1 and 99.

5. If p is an integer greater than 1, then p and p-1 are coprime, for example, 57 and 56.

6. If p is an odd integer greater than 1, then p and p-2 are coprime, for example, 17 and 15.

03

Euler’s Function

Consider the following question:

Given any positive integer n, how many positive integers less than or equal to n are coprime with n? (For example, how many numbers are coprime with 8 from 1 to 8?)

The method to calculate this value is called Euler’s Function, denoted as φ(n). Among the numbers from 1 to 8, those that are coprime with 8 are 1, 3, 5, and 7, so φ(n) = 4.

The calculation of φ(n) is not complicated, but to obtain the final formula, we need to discuss it step by step.

First case

If n=1, then φ(1) = 1. Because 1 is coprime with any number (including itself).

Second case

If n is prime, then φ(n)=n-1. Because a prime number is coprime with every number less than it. For example, 5 is coprime with 1, 2, 3, and 4.

Third case

If n is a power of a prime, that is, n = p^k (p is prime, k is an integer greater than or equal to 1), then

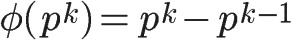
For example, φ(8) = φ(2^3) =2^3 – 2^2 = 8 -4 = 4.

This is because only when a number does not contain the prime p can it be coprime with n. The numbers containing the prime p total p^(k-1), that is, 1×p, 2×p, 3×p, …, p^(k-1)×p, removing them leaves the numbers that are coprime with n.

The above expression can also be written in the following form:

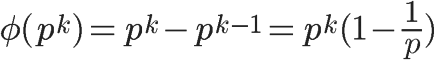
It can be seen that the second case above is a special case when k=1.

Fourth case

If n can be factored into the product of two coprime integers,

n = p1 × p2

then

φ(n) = φ(p1p2) = φ(p1)φ(p2)

That is, the Euler function of a product equals the product of the Euler functions of each factor. For example, φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24.

The proof of this requires the use of the “Chinese Remainder Theorem“, which I will not elaborate on here, just briefly mention the idea: If a is coprime with p1 (a<p1), b is coprime with p2 (b<p2), and c is coprime with p1p2 (c<p1p2), then c corresponds one-to-one with the pair (a,b). Since a has φ(p1) possible values and b has φ(p2) possible values, the pair (a,b) has φ(p1)φ(p2) possible values, and c has φ(p1p2) possible values, so φ(p1p2) equals φ(p1)φ(p2).

Fifth case

Because any integer greater than 1 can be expressed as a product of a series of primes.

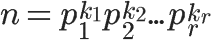
Based on the conclusion of the fourth case, we get

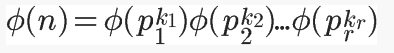
Then based on the conclusion of the third case, we get

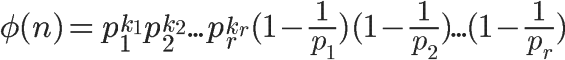
It also equals

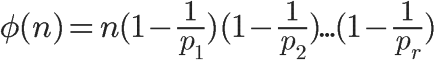
This is the general calculation formula for Euler’s function. For example, the calculation process of the Euler function for 1323 is as follows:

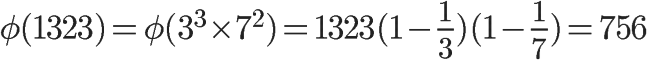
04

Euler’s Theorem

The usefulness of Euler’s function lies in Euler’s Theorem. “Euler’s Theorem” states that:

If two positive integers a and n are coprime, then the Euler function φ(n) can make the following equation hold:

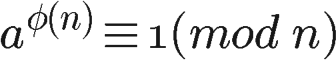
In other words, a raised to the φ(n) power gives a remainder of 1 when divided by n. Or, a raised to the φ(n) power minus 1 is divisible by n. For example, 3 and 7 are coprime, and the Euler function φ(7) equals 6, so 3 raised to the 6th power (729) minus 1 is divisible by 7 (728/7=104).

The proof of Euler’s theorem is quite complex, so I will omit it. We just need to remember its conclusion.

Euler’s theorem can greatly simplify certain calculations. For example, 7 and 10 are coprime, according to Euler’s theorem,

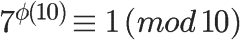
Since φ(10) equals 4, we can immediately conclude that the last digit of 7 raised to any multiple of 4 must be 1.

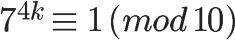
Therefore, the last digit of any power of 7 (for example, 7 raised to the 222nd power) can be calculated mentally.

Euler’s theorem has a special case.

Assuming the positive integer a is coprime with the prime p, since the φ(p) of the prime p equals p-1, Euler’s theorem can be written as

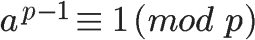
This is the famous Fermat’s Little Theorem. It is a special case of Euler’s theorem.

Euler’s theorem is the core of the RSA algorithm. Understanding this theorem allows one to understand RSA.

05

Modular Inverse Element

There is one last concept remaining:

If two positive integers a and n are coprime, then there exists an integer b such that ab-1 is divisible by n, or in other words, the remainder of ab when divided by n is 1.

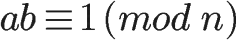
In this case, b is called the “modular inverse element” of a.

For example, if 3 and 11 are coprime, then the modular inverse element of 3 is 4, since (3 × 4)-1 can be divided by 11. Clearly, there are multiple modular inverse elements; 4 plus or minus any integer multiple of 11 are all modular inverse elements of 3 {…,-18,-7,4,15,26,…}, that is, if b is a modular inverse element of a, then b+kn is also a modular inverse element of a.

Euler’s theorem can be used to prove the existence of the modular inverse element.

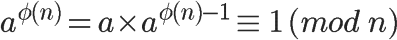
It can be seen that the φ(n)-1 power of a is the modular inverse element of a.

Alright, all the necessary mathematical tools have been introduced.

Source: Scientific Squirrel Association

∑ Edited / Douzhi