With the rise of modern cryptography, the design principles of cryptographic algorithms have shifted from algorithm secrecy to algorithm openness. At the same time, the role of cryptography is no longer limited to ensuring the confidentiality of information; the demand for cryptographic technology to ensure the integrity, authenticity, and non-repudiation of information is continuously increasing. The public key cryptography system, or asymmetric cryptography system, has begun to emerge, and public key cryptography is a highly distinctive and crucial component of modern cryptography.
In 1976, Whitfield Diffie and Martin Hellman published a scheme for key exchange using a public key system, which discussed methods for establishing secure channels in insecure communication environments. This is regarded as the beginning of the entire public key cryptography system. When this scheme is implemented in the modular exponentiation group over finite fields, it becomes the well-known Diffie-Hellman key exchange.
In 1977, Ron Rivest, Adi Shamir, and Leonard Adleman from MIT proposed the RSA algorithm based on the difficulty of factoring large integers, named after the initials of their names. To this day, the RSA algorithm remains one of the most mainstream public key systems.
In 1985, Neal Koblitz and Victor S. Miller proposed a method for elliptic curve (EC) encryption. The ECC algorithm began to be widely used from 2004 to 2005, gaining widespread recognition due to its high efficiency and difficulty.
In 1984, A. Shamir proposed the concept of Identity-Based Cryptography (IBC), where the user’s public key is uniquely determined by the user’s identity and does not require a third-party CA to protect the authenticity of the public key. However, the scheme for constructing the IBC algorithm using elliptic curves was not discovered until the early 21st century.
Cryptography is a crucial tool for the nation, and the localization of cryptography is an essential path to maintaining national security. In the process of cryptography localization in China, the SM2 public key cryptography algorithm based on ECC theory and the SM9 identity-based cryptography algorithm based on elliptic curve pairs were successively introduced in 2010 and 2016. In November 2018, China’s SM2/SM9 digital signature algorithm officially became an ISO/IEC international standard, marking the preliminary formation of China’s international standard system for cryptographic algorithms and reflecting the advanced level of China’s cryptographic technology.
Public key cryptography relies on the establishment of one-way functions. The one-way nature of one-way functions is computationally significant, similar to the unidirectional conductivity of a physical diode; the forward operation is relatively easy to compute, while the inverse operation is computationally difficult. This one-way nature is the basis for constructing public key algorithms. Based on the differing properties of public and private keys, private key operations are used for digital signatures and asymmetric decryption, while public key operations are used for signature verification and asymmetric encryption. Due to the characteristics of public and private keys, the key management process and resources are simplified significantly. For example, in a system with 10 entities, symmetric cryptography would require establishing at least 45 keys to achieve secure pairwise transmission, while public key cryptography only requires 10 pairs of keys.
Public key cryptography can be used for encryption but is not intended to replace symmetric cryptography. This is because using public key encryption alone is far less efficient than symmetric algorithms, which is clearly not cost-effective. In fact, in cryptographic applications, symmetric algorithms, public key algorithms, and hash algorithms are often used to form an algorithm suite. Public key cryptography provides solutions for establishing symmetric keys, such as digital envelopes and key agreement, while also serving an authentication role, primarily achieved through digital signatures combined with certificate systems. A complete public key cryptography system includes at least a digital signature algorithm and a public key encryption algorithm, and some may also include key agreement protocols. Common public key cryptography systems include ElGamal, RSA, ECC, and IBC.

The ElGamal public key system is based on the discrete logarithm problem. The concept of discrete logarithm is defined on groups. Given a group G(A,•) and elements a and b, the integer k that satisfies ak=b can be denoted as k=logab (of course, this notation is only for understanding; it is not written this way in practice). The meaning of ‘logarithm’ is reflected in the above expression, while the meaning of ‘discrete’ is embodied in k being an integer. To make k unique, it can be restricted to the range from 0 to N-1, where N is the order of group G.
The discrete logarithm problem in cryptography often refers to the following typical problem: in the multiplicative group modulo p generated by r, where p is a sufficiently large prime number and n is a positive integer less than p, given rk≡n(mod p), finding the exponent k is difficult. This is because this group is relatively simple, easy to implement, and can fully reflect the intrinsic meaning of the ElGamal system. In the above description, when p is sufficiently large, it allows not taking the generator r as the base, but still requires that the order of the chosen base is sufficiently close to p, as the size of the order of r determines the security of the system.
The ElGamal system also includes key agreement protocols, the most typical of which is the Diffie-Hellman (DH) protocol. In fact, the DH protocol is the beginning of the entire public key cryptography idea. To ensure forward security, DH can be improved to DHE, where “E” stands for “Ephemeral,” meaning “temporary.” Additionally, since cyclic groups have good arithmetic properties, the number of key agreement participants can be expanded from two to multiple.
RSA
The RSA public key system is based on the problem of factoring large integers and the RSA problem. Currently, no polynomial-time method has been found for factoring large integers. The RSA problem refers to the difficulty of recovering the plaintext m given the RSA public key (n, e) and the ciphertext c≡me(mod n).
Generating RSA keys is a crucial part of the entire algorithm and also a challenging implementation. RSA keys are generated as follows:
1. Choose two distinct prime numbers p and q. Large primes can be effectively found through primality testing. For security, p and q are usually constrained to have a certain difference in digits. p and q must be kept secret.
2. Compute n=pq. n is the modulus, and its length is the key length. n is publicly shared as part of the key.
3. Compute the Carmichael function λ(n)=lcm(λ(p),λ(q)). Since p and q are prime, λ(p)=φ(p)=p-1 and λ(q)=φ(q)=q-1, thus λ(n)= lcm(p-1,q-1). λ(n) must be kept secret.
4. Choose an integer e such that 1<e<λ(n) and gcd(e,λ(n))=1 (i.e., e is coprime to λ(n)). A shorter length for e is beneficial for encryption, often taken as 65537. e is publicly shared as the public key exponent.
5. Compute d≡e-1(mod λ(n)), which also means d•e≡1(mod λ(n)). d can be calculated using the extended Euclidean algorithm. d is kept secret as the private key exponent.
6. Note: Initially, the Euler function φ(n)=(p-1)(q-1) was used instead of λ(n) to calculate the private key exponent d. Since λ(n) divides φ(n), this method can also satisfy step 5, but occasionally d>λ(n) may occur. Additionally, due to the symmetry of the modular inverse operation in step 5, there is also a method of first selecting the private key exponent d and then calculating the public key exponent e.
Below is an example of the RSA encryption and decryption process. Suppose B wants to send a message to A using the RSA algorithm, with the message M transformed into an integer and subjected to standardized padding and block operations, resulting in m. For ease of narration, let’s assume 0≤m<n.
Encryption: B obtains A’s public key (n, e) and computes the ciphertext c: me≡c(mod n). B sends the ciphertext c to A.
Decryption: A receives the ciphertext c and uses his private key exponent d to restore the plaintext m: cd≡(me)d≡m(mod n).
ECC
The ECC public key system is based on the elliptic curve discrete logarithm problem, which is the difficulty of finding multiples given a base point and its multiple points. The operation of multiple points is relatively easier; let k be the multiple, 2n-1<k≤2n, by using methods like binary expansion, the complexity can be reduced from O(2n) to O(n).
An elliptic curve is a type of cubic curve, for example, the elliptic curve equation over a finite field is defined as y2=x3+ax+b. Given a line intersecting this curve, the solutions to the two equations are points P, Q, and R, and the addition of points on the elliptic curve satisfies P+Q+R=0. One typical image of an elliptic curve is shown below:
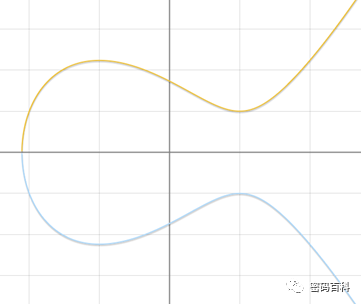
This curve is smooth everywhere, and when two points P and Q are taken on the curve, the line connecting them intersects the elliptic curve in several scenarios:
1. Two distinct points, the line intersects the curve at a third point R. This corresponds to the elliptic curve point addition operation: P+Q=-R.
2. Two identical points, the line intersects the curve at another point R. When the two points are identical, the line is tangent to the curve at the chosen point, which corresponds to the elliptic curve doubling operation: P+R=P+P=-R.
3. Two distinct points, the line intersects the curve at only these two points. This situation indicates that the line is tangent to the curve, where one point is the tangential point, similar to scenario 2.
4. Two identical points, the line intersects the curve at a unique point, at which the third point is taken as the point at infinity 0. For the above curve, the tangential point is the intersection of the curve with the x-axis. P+Q+R=P+P+0=2P=0.
The above is viewed from the perspective of curve analysis, while when the elliptic curve is restricted to a finite field, only a finite number of integer points satisfy the equation. At this point, the elliptic curve forms a finite abelian group, and point operations on the curve are truly established from here. The following image shows the distribution of points on a curve under finite fields of different orders, which bears no resemblance to the previous image.
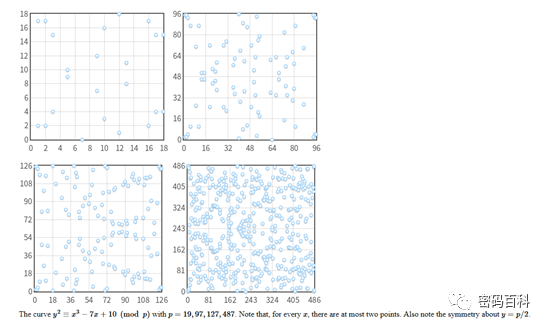
The choice of the curve in the ECC system is crucial, including the parameters of the curve, the size of the base field, and the selection of the base point, among others. Common digital signature algorithms in the ECC system include ECDSA, and key agreement protocols include ECDH and ECDHE. China’s independently designed SM2 algorithm is a complete ECC system that includes digital signature algorithms, public key encryption algorithms, and key exchange protocols, and selects a 256-bit curve over a finite field.

IBC stands for “Identity-Based Cryptography.” Compared to certificate-based public key systems, the user’s public key is uniquely determined by the user’s identity and does not require a third-party CA to issue a certificate to ensure the authenticity of the public key. The private key is computed by a Key Generation Center (KGC) based on the master key and the user’s identity. Of course, this implies that for an identity-based cryptography system, the KGC must be absolutely secure.
One implementation of IBC is constructed using elliptic curves, such as the domestic SM9 algorithm. When the difficulty of solving the elliptic curve discrete logarithm problem and the extension field discrete logarithm problem is comparable, IBC constructed using elliptic curves can balance security and implementation efficiency.
The above briefly introduced four public key systems, which are not entirely on the same level. The ElGamal system constructs public key cryptography using group theory without specifying which group and group operation; it was initially applied to finite fields, and in fact, the ECC system can be seen as an application of the ElGamal system in the elliptic curve group. IBC arises from practical application needs, proposing the structure of an identity-based cryptography system without restricting how to implement it. When IBC is implemented using elliptic curve theory (like SM9), it is differentiated from the usual ECC theoretical system. The ECC system is relatively more specific; however, using the same theoretical foundation, there are various implementations. From a macro perspective, RSA is the most concrete and least extensible public key system.
Of course, in most scenarios such as financial systems and network communications, RSA remains the most widely used public key system. From the perspective of efficiency and security, RSA is inferior to ECC. It is estimated that the security of a 2048-bit RSA modulus is roughly equivalent to that of a 256-bit ECC curve, at which point the efficiency is far inferior. With the improvement of computational power and the advancement of attack methods, the currently accepted RSA modulus length is at least 2048 bits, with examples of even 4096 bits in applications. With the continuous breakthroughs in quantum computing, hard cracking becomes possible, and research on quantum cryptography and post-quantum cryptography is urgent.
Follow Us

