
Many people are interested in cryptography, so today I will take you on a journey to explore how numbers are encrypted.
1
Let’s start with a little game. You think of a number, say 3; I will think of a number, say 5. Let’s keep our numbers secret from each other.
How can we send messages to each other without anyone else finding out?
To send a message, we inevitably have to use some public channels. Suppose there is a public number 7, and there is an observer named Xiao Ming. How can we get around him?
We multiply the number we are thinking of by this public number 7. You have 3, so 3 multiplied by 7 is 21, and you will announce 21; I have 5, so 5 multiplied by 7 is 35, and I will announce 35.
Then, I will use the number you announced, 21, and multiply it by my number 5, resulting in 105; you will use my announced 35 and multiply it by your number 3, also resulting in 105.
This is our shared password.
Even if Xiao Ming sees the numbers 7, 21, and 35, he cannot deduce the secret numbers we are thinking of, nor can he derive our shared password.
You might say this is too simple and easy to see through. So let me introduce you to a more complex example and let you appreciate the fun of encryption algorithms.
2
You may not have heard of “clock arithmetic”, but you have definitely seen a clock. Every time the hand passes 12, it starts again from 1.
The principle of clock arithmetic is similar, except we replace 12 with 0, and the size of the clock can be defined by ourselves.
For example, here is a clock of size 11:
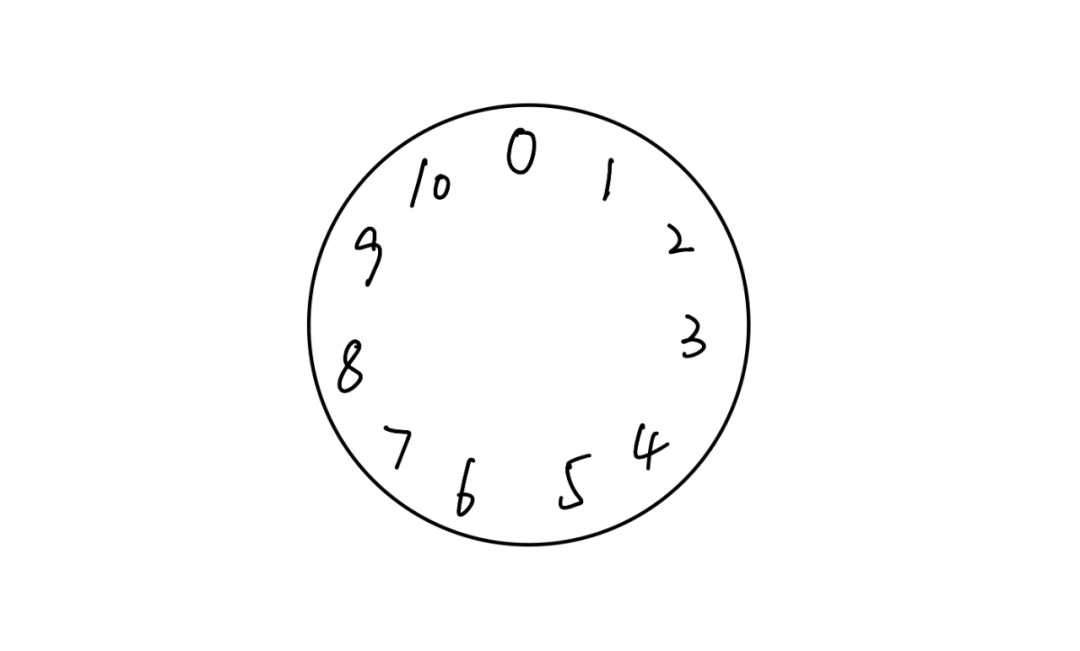
How do we use this clock?
For example, calculating 11 + 1, which is originally 12, we divide by the size of the clock 11, and the final remainder is 1, so we consider 11 + 1 = 1. This is the first layer of encryption.
Next, we create a table:
| n | 2^n | 4^n | 7^n |
|
1 |
2 | 4 | 7 |
| 2 | 4 | 5 | 5 |
| 3 | 8 | 9 | 2 |
| 4 | 5 | 3 | 3 |
| 5 | 10 | 1 | 10 |
| 6 | 9 | 4 | 4 |
| 7 | 7 | 5 | 6 |
| 8 | 3 | 9 | 9 |
| 9 | 6 | 3 | 8 |
| 10 | 1 | 1 | 1 |
In this table, we calculated the remainder of n from 1 to 10 for 2^n, 4^n, and 7^n divided by 11. Based on this table, we perform the second layer of encryption.
Then, we each select a number, say you choose 2 and I choose 7. We need to announce the size of the clock and our chosen bases.
The size of this clock is 11, and let’s choose the base as 2.
Next, we find the remainders of 2^2 and 2^7 divided by 11 in the table, which are 4 and 7 respectively.
These two numbers can also be announced, so we have a total of 4 public numbers: 11, 2, 4, and 7.
To outsiders, this looks completely confusing. How do we get our shared password?
We still use the numbers announced by each other. You announced 4, so I calculate 4^7 (the number I initially chose) divided by 11, which gives a remainder of 5; I announced 7, so you calculate 7^2 (the number you initially chose) divided by 11, which also gives a remainder of 5.
This number is our shared key.
3
The above two examples illustrate how to create the same shared key.
So what is the use of this shared key?
With it, we can use simple addition and subtraction to extract information while ensuring that outsiders cannot decipher it at all.
For example, in the second example, the shared key is 5. Now there is a new piece of information 8. If you want to pass this information to the other party, you just need to add 8 and 5 to get 13.
Just announce this number, and the other party just needs to subtract the shared key to decrypt the information. However, anyone without the shared key will get it wrong even if they receive this information.

If you also want to have a diverse thinking model, feel free to join my community. Limited time offer: 199 (only 50 spots available), scan the code for details:
