This article is a highlight from the Kanxue Forum.
Author from Kanxue ForumID: TkBinary
-
Table of Contents
-
Series Articles
-
1. Supplementary Mathematical Knowledge
-
1.1 Introduction
-
1.2 Fractions
-
1.2.1 Fraction Addition
-
1.2.2 Fraction Multiplication
-
2. Division Optimization for Signed Non-Power-of-Two
-
2.1 Advanced Code and Disassembly
-
2.2 Restoration of Non-Power-of-Two Division
-
2.3 Optimization and Principles for Non-Power-of-Two Divisors
-
2.4 Summary of Division Restoration Formulas
-
3. Division Optimization for Unsigned Non-Power-of-Two
-
3.1 Restoration of Positive Unsigned Non-Power-of-Two Divisor Code
-
3.2 Restoration of Negative Unsigned Non-Power-of-Two Divisor Code
-
3.3 Special Assembly
-
4. Why Learn Division Optimization
-
4.1 Why Learn Division Optimization
-
5. Advanced Vs Compiler and GCC Optimization under Linux
-
5.1 vs2019 x86 Signed Non-Power-of-Two Optimization
-
5.2 vs2019 x64 Signed Non-Power-of-Two Optimization
-
5.3 Linux GCC x86 Signed Non-Power-of-Two
-
5.4 Other Similar Projects for Research
Series ArticlesFamiliarity with IDA Tools in Disassembly Technologyhttps://bbs.pediy.com/thread-224499.htmReverse Engineering Technology for Finding Main Entry Pointshttps://bbs.pediy.com/thread-224500.htm
Restoration of Disassembled Code Optimization Methods
Restoration of Disassembled Code for Power-of-Two Divisors
Restoration of Disassembled Code for Addition, Subtraction, and Multiplication
* Click the text to jump to the article
1. Supplementary Mathematical Knowledge
1.1 Introduction
In the optimization of division for non-power-of-two, the method used is to convert division into multiplication. When learning this knowledge, we first need to understand some basic mathematical concepts, which will also help us understand the formulas.
1.2 Fractions
1.2.1 Fraction Addition
Fraction addition: For fractions with the same denominator, add the numerators while keeping the denominator unchanged. For example: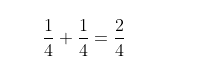
For fractions with different denominators, if you want to add them, you need to find the least common denominator. The common denominator refers to when two or more fractions have the same denominator, they share a common denominator. Note that this is a common denominator, not the least common denominator; the least common denominator refers to the smallest common denominator among two or more fractions.Finding the least common denominator: We can list the multiples of the denominators. If there are two fractions, list the multiples of both denominators, find the common multiples, and then make them equivalent.For example:
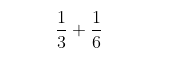List the multiples of 3: 3, 6, 9, 12, 15, …List the multiples of 6: 6, 12, 18, 24, …We find that the least common multiple is 6, so we multiply both the numerator and denominator by 2 to convert them to the same denominator and then add them.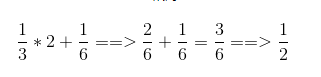
1.2.2 Fraction Multiplication
Fraction multiplication
**Fraction * Fraction = Numerator * Numerator / Denominator * Denominator**As follows:
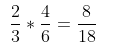
Mnemonic: Multiplying fractions is not difficult; multiply the numerators and the denominators, then simplify.
Multiplying an integer
If an integer is multiplied by a fraction, the fraction can be viewed as a numerator, while the denominator is 1.
Example:
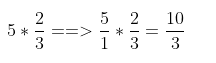
As for simplification, you can find the greatest common factor, which is the opposite of finding common multiples.
Common multiples are found by multiplication, while common factors are found by identifying numbers that can divide both the numerator and denominator, removing the same number.
2. Division Optimization for Signed Non-Power-of-Two
2.1 Advanced Code and Disassembly
int main(int argc, char* argv[]){ /* Division */ int NumberOne = 0; int NumberTwo = 0;
scanf("%d",&NumberOne); scanf("%d",&NumberTwo);
int Count1 = NumberOne / 3;
int Count2 = NumberTwo / 5;
int Count3 = NumberTwo / 6;
int Count4 = NumberTwo / 9;
printf("%d%d%d%d%d",Count4,Count3,Count2,Count1); system("pause");
return 0;}Corresponding assembly code:
.text:00401000 ; int __cdecl main(int argc, const char **argv, const char **envp).text:00401000 _main proc near ; CODE XREF: start+AF↓p.text:00401000.text:00401000 var_8 = dword ptr -8.text:00401000 var_4 = dword ptr -4.text:00401000 argc = dword ptr 4.text:00401000 argv = dword ptr 8.text:00401000 envp = dword ptr 0Ch.text:00401000.text:00401000 sub esp, 8.text:00401003 xor eax, eax.text:00401005 mov [esp+8+var_8], eax.text:00401009 mov [esp+8+var_4], eax.text:0040100D lea eax, [esp+8+var_8].text:00401011 push eax.text:00401012 push offset aD ; "%d".text:00401017 call _scanf.text:0040101C lea ecx, [esp+10h+var_4].text:00401020 push ecx.text:00401021 push offset aD ; "%d".text:00401026 call _scanf
//First segment.text:0040102B mov ecx, [esp+18h+var_8].text:0040102F mov eax, 55555556h.text:00401034 imul ecx.text:0040103A mov eax, edx.text:0040103C shr eax, 1Fh.text:0040103F add edx, eax
//Second segment.text:00401036 mov ecx, [esp+18h+var_4].text:00401041 mov eax, 66666667h.text:00401047 imul ecx.text:00401049 sar edx, 1.text:0040104B mov eax, edx.text:0040104D shr eax, 1Fh.text:00401050 add edx, eax.text:00401057 push edx //Here the original pipeline optimization was mentioned above//Third segment.text:00401052 mov eax, 2AAAAAABh.text:00401058 imul ecx.text:0040105A mov eax, edx.text:0040105C shr eax, 1Fh.text:0040105F add edx, eax.text:00401066 push edx //Same as above pipeline optimization
//Fourth segment.text:00401061 mov eax, 38E38E39h.text:00401067 imul ecx.text:00401069 sar edx, 1.text:0040106B mov ecx, edx.text:0040106D shr ecx, 1Fh.text:00401070 add edx, ecx.text:00401072 push edx
.text:00401073 push offset aDDDDD ; "%d%d%d%d%d".text:00401078 call _printf.text:0040107D push offset aPause ; "pause".text:00401082 call _system.text:00401087 xor eax, eax.text:00401089 add esp, 30h.text:0040108C retn.text:0040108C _main endp2.2 Restoration of Non-Power-of-Two Division
At first glance, the assembly code above shows how division has transformed into this, with both multiplication and division present, along with adjustments. Here, we will focus on explaining this.
If we want to restore directly, we can extract the code template and perform the restoration directly.
Code template:
mov ecx, Dividend
mov eax, M_value
imul ecx
sar edx, n
mov eax, edx
shr eax, 1Fh
add edx, eax
push edxAccording to the assembly, we only need to look at three points and derive the formulas for these three points:
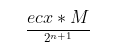
Where M is calculated by the compiler, ecx is the dividend, and here sar n value directly operates on edx. Here, division is actually transformed into multiplication, and if division is transformed into multiplication, then in the 32-bit era, multiplying two numbers by 32 will not overflow. Therefore, we actually use edx, eax to represent the result of multiplication, and we directly operate on the high part of the product, where right shifting by 1 is equivalent to dividing by 2^n + 1.
So when restoring, just remember the fixed formula: 2^32 + 1/M.
Directly count the value of n, and use 2 raised to the 32nd power + n. Because the low part of the product represents 2 raised to the 32nd power, we directly operate on the high part of the product, so we need to add the value of the low part of the 32nd power.
Example restoration:
.text:0040102B mov ecx, [esp+18h+var_8].text:0040102F mov eax, 55555556h.text:00401034 imul ecx.text:0040103A mov eax, edx //Here we directly use edx without modifying it. So our n value is 0.text:0040103C shr eax, 1Fh.text:0040103F add edx, eaxWe apply the formula:
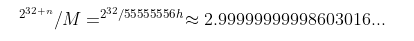2.99 rounded up = 3, so we find that the divisor is 3.
2.3 Optimization and Principles for Non-Power-of-Two Divisors
First, let’s look at our assembly:
.text:00401061 mov eax, 38E38E39h.text:00401067 imul ecx.text:00401069 sar edx, 1.text:0040106B mov ecx, edx
.text:0040106D shr ecx, 1Fh.text:00401070 add edx, ecx.text:00401072 push edxHere, our assembly is divided into two parts. The upper part can be directly applied to the formula for restoration, while the lower part is actually obtaining the sign bit and adjusting it. shr logically right shifts and fills the highest bit with 0, right shifting by 31 (1F) to obtain the sign bit, and then there is an addition. This addition is also a pattern, similar to what we discussed earlier about branchless optimization.If the result is positive, then add edx, eax is just adding 0, which means doing nothing; if the result is negative, we need to adjust the quotient of the division by adding 1.The principle of converting division into multiplicationIf you want to understand why the non-power-of-two code transforms into the above code, we need to understand the principle.Let a = Dividend, b = Divisor (a constant value)Then we will have the following formula: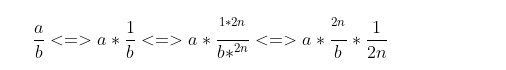
This is what we understood about fractions.Looking at the final formula:
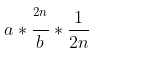Where 2^n/b can be calculated at compile time, VC++6.0 or VS2019 during compilation, the value of n is greater than 32, so it can be calculated.Thus, our formula can be transformed as follows, where we denote the value that the compiler can calculate as C. Therefore, we can derive the following formula:
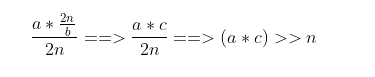Ultimately simplified to (a * c) >> n, and looking back at our assembly code:
.text:00401061 mov eax, 38E38E39h.text:00401067 imul ecx.text:00401069 sar edx, 1Listing the formula:ecx = Dividendeax = M equivalent to the value of 2^n/b.ecx eax / 2^33 This formula corresponds exactly to our principle of converting division into multiplication, and is the same as our previous formula, (a c) >> n.So we can solve the equation, 2^n / b = M value, then 2^n / M = b, where b is our required divisor, thus deriving our divisor.
2.4 Summary of Division Restoration Formulas
Restoration formula for division: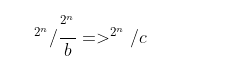
Here, C is actually 2^n/b, which we also set as M in assembly, so it can also be written as follows:
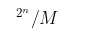The formula for converting division into multiplication:
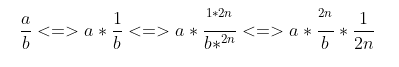Transforming to:
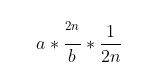Continuing the transformation:
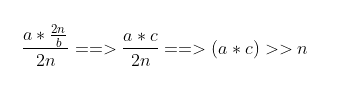Final transformation:
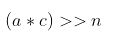For the above, remembering the code template can also allow for restoration, but understanding the principle of converting division into multiplication is even better. Looking at the characteristics of advanced code, we find that they are all similar, and can use the formula for converting division into multiplication for restoration. The restoration formula for division is essentially solving the equation, and solving it will yield the dividend.3. Division Optimization for Unsigned Non-Power-of-TwoAdvanced code:
int main(int argc, char* argv[]){ /* Division */ unsigned int NumberOne = 0; unsigned int NumberTwo = 0;
scanf("%u",&NumberOne); scanf("%u",&NumberTwo);
unsigned int Count1 = NumberOne / 3;
unsigned int Count2 = NumberTwo / 5;
unsigned int Count3 = NumberTwo / 6;
unsigned int Count4 = NumberTwo / 9;
printf("%d%d%d%d%d",Count4,Count3,Count2,Count1); system("pause");
return 0;}Assembly code:
.text:00401005 mov [esp+8+var_8], eax.text:00401009 mov [esp+8+var_4], eax
.text:0040102B mov eax, 2863311531.text:00401030 mov ecx, [esp+18h+var_4].text:00401034 mul [esp+18h+var_8].text:00401038 shr edx, 1
.text:0040103A mov eax, 3435973837.text:0040103F push edx.text:00401040 mul ecx.text:00401042 shr edx, 2
.text:00401045 mov eax, 0AAAAAAABh.text:0040104A push edx.text:0040104B mul ecx.text:0040104D shr edx, 2
.text:00401050 mov eax, 38E38E39h.text:00401055 push edx.text:00401056 mul ecx.text:00401058 shr edx, 1.text:0040105A push edx3.1 Restoration of Positive Unsigned Non-Power-of-Two Divisor Code
Looking at the code above, based on the formula for converting division into multiplication (a * b) >> n, we can derive: 2^n / b = M 2^n/M = b(divisor constant) Here, it is just changed to unsigned. The restoration formula remains the same. For example:
.text:0040102B mov eax, 2863311531.text:00401030 mov ecx, [esp+18h+var_4].text:00401034 mul [esp+18h+var_8].text:00401038 shr edx, 1Taking N value = 1, taking M value = 2863311531 (Note that here I pressed H in IDA to convert to decimal for easier calculations). Operating on edx, so:
Dividend = 2^33 Divisor = M Find divisor formula = 2^n/M = b Substitute into the formula 2^33 / 2863311531 = 2.999999999 rounded up = 3, so we find that the divisor is 3. ecx = var4, so the disassembly for advanced code is var_4 / 33.2 Restoration of Negative Unsigned Non-Power-of-Two Divisor Code
Advanced code as follows:
int main(int argc, char* argv[]){ /* Division */ unsigned int NumberOne = 0; unsigned int NumberTwo = 0;
scanf("%u",&NumberOne); scanf("%u",&NumberTwo);
unsigned int Count1 = NumberOne / -3;
unsigned int Count2 = NumberTwo / -5;
unsigned int Count3 = NumberTwo / -6;
unsigned int Count4 = NumberTwo / -9;
printf("%d%d%d%d%d",Count4,Count3,Count2,Count1); system("pause");
return 0;}Core code disassembly segment:
.text:00401005 mov [esp+8+var_8], eax.text:00401009 mov [esp+8+var_4], eax
/-3.text:0040102B mov eax, 40000001h.text:00401030 mov ecx, [esp+18h+var_4].text:00401034 mul [esp+18h+var_8].text:00401038 shr edx, 1Eh.text:00401040 push edx
/-5.text:0040103B mov eax, 80000003h.text:00401041 mul ecx.text:00401043 shr edx, 1Fh.text:0040104B push edx
/-6.text:00401046 mov eax, 7.text:0040104C mul ecx.text:0040104E mov eax, ecx.text:00401050 sub eax, edx.text:00401052 shr eax, 1.text:00401054 add eax, edx.text:00401056 shr eax, 1Fh.text:00401059 push eax/-9.text:0040105A mov eax, 80000005h.text:0040105F mul ecx.text:00401061 shr edx, 1Fh.text:00401064 push edxCode TemplateBased on the disassembled code above, we see three places with our suspected (a * c) >> n code, which is the formula for converting division into multiplication.We can randomly take one place and substitute it into the formula for restoration:Let M = 40000001h = 10 in decimal 1073741825Let n = 1E = 10 in decimal 30Then substitute into our restoration formula: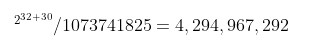
The value calculated using a scientific calculator is 4294967292 (in decimal). Then we copy this number into a programmer’s calculator (paste into Dec 10 decimal input) and can see it is a negative number.
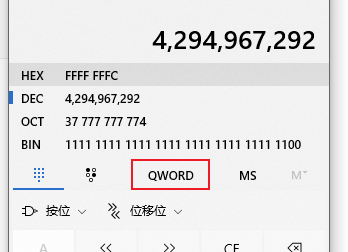Note that when inputting, use QWORD input, then click to convert to DWORD to see it expressed as -4.
At this point, directly taking the NOT will yield the original dividend, but this dividend constant is negative.
You can also adjust this value by +1 to become 4294967293, thus directly obtaining -3, making it clear that our dividend is -3.
3.3 Special Assembly
Looking at the above code, we particularly do not understand why the /-6 assembly has changed. These will be explained in detail in a later special topic on how to restore. Now we can look at my calculation: 2^64 / 4,294,967,302 = 0x100000006, the highest bit is the sign bit, indicating this is a negative number, which is -6. If we restore according to the template, the result is 0xFFFFFFF9, and then taking the NOT gives us 6. But there is also a code template:
mov regA,[ebp - xxx]mov reg,Mmul regAsub regA,edxshr regA,nadd regA,edxshr regA,(n-1)Looking at the code template, we can derive:Multiply, subtract, shift, add, shift. This can be restored using the template:
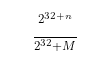
Here, taking out two n values, 1+31= 32, so n value is 32.
Substituting into the formula yields:
2^64 / 4,294,967,303 = 0XFFFFFFF9
Regarding special assembly, it should be explained in detail in the next article.
4. Why Learn Division Optimization
4.1 Why Learn Division Optimization
Still, the question remains: why learn division optimization? Let’s take our previous example as an illustration, using IDA F5 to view.
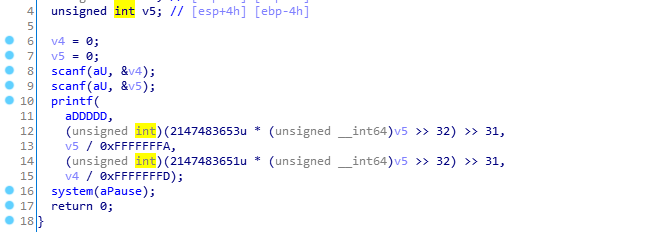
When you see such code, are you scared? Directly disassembling can yield this segment of code, and using IDA disassembly will show right shifts, etc. In our view, this is hard assembly.
It is also about restoring it with a hard head, so this is the significance of our learning. Of course, F5 is still very powerful, but learning it will better help us with disassembly and restore it to high-level code.
5. Advanced Vs Compiler and GCC Optimization under Linux
In fact, it is still the same old story, comparing high versions with low versions to see if the optimization methods have changed.
5.1 vs2019 x86 Signed Non-Power-of-Two Optimization
Advanced code:
int main(int argc, char* argv[]){ /* Division */ int NumberOne = 0; int NumberTwo = 0; scanf("%d",&NumberOne); scanf("%d",&NumberTwo); int Count1 = NumberOne / 3; int Count2 = NumberTwo / 5; int Count3 = NumberTwo / 6; int Count4 = NumberTwo / 9; printf("%d%d%d%d%d",Count4,Count3,Count2,Count1); system("pause"); return 0;}Assembly:
.text:00401080 push ebp.text:00401081 mov ebp, esp.text:00401083 sub esp, 8.text:00401086 lea eax, [ebp+var_4].text:00401089 mov [ebp+var_4], 0.text:00401090 push eax.text:00401091 push offset unk_41ECDC.text:00401096 mov [ebp+var_8], 0.text:0040109D call sub_401050.text:004010A2 lea eax, [ebp+var_8].text:004010A5 push eax.text:004010A6 push offset unk_41ECDC.text:004010AB call sub_401050 .text:004010B0 mov ecx, [ebp+var_8].text:004010B3 mov eax, 55555556h.text:004010B8 imul [ebp+var_4].text:004010BB mov eax, edx.text:004010BD shr eax, 1Fh.text:004010C0 add eax, edx.text:004010C2 push eax .text:004010C3 mov eax, 66666667h.text:004010C8 imul ecx.text:004010CA sar edx, 1.text:004010CC mov eax, edx.text:004010CE shr eax, 1Fh.text:004010D1 add eax, edx.text:004010D3 push eax .text:004010D4 mov eax, 2AAAAAABh.text:004010D9 imul ecx.text:004010DB mov eax, edx.text:004010DD shr eax, 1Fh.text:004010E0 add eax, edx.text:004010E2 push eax .text:004010E3 mov eax, 38E38E39h.text:004010E8 imul ecx.text:004010EA sar edx, 1.text:004010EC mov eax, edx.text:004010EE shr eax, 1Fh.text:004010F1 add eax, edx.text:004010F3 push eax.text:004010F4 push offset aDDDDD ; "%d%d%d%d%d".text:004010F9 call sub_401020.text:004010FE push offset aPause ; "pause".text:00401103 call sub_4048E7.text:00401108 add esp, 28h.text:0040110B xor eax, eax.text:0040110D mov esp, ebp.text:0040110F pop ebpHere, pipeline optimizations are not removed, and it can be seen that there is no difference from VC6.0.
5.2 vs2019 x64 Signed Non-Power-of-Two Optimization
Advanced code:
int main(int argc, char* argv[]){ /* Division */ __int64 NumberOne = 0; __int64 NumberTwo = 0; scanf("%I64d", &NumberOne); scanf("%I64d", &NumberTwo); __int64 Count1 = NumberOne / 3; __int64 Count2 = NumberTwo / 5; __int64 Count3 = NumberTwo / 6; __int64 Count4 = NumberTwo / 9; printf("%I64d%I64d%lld%lld", Count4, Count3, Count2, Count1); system("pause"); return 0;}Disassembly:
text:00000001400010D0 sub rsp, 38h.text:00000001400010D4 xor eax, eax.text:00000001400010D6 lea rdx, [rsp+38h+arg_10].text:00000001400010DB lea rcx, aI64d ; "%I64d".text:00000001400010E2 mov [rsp+38h+arg_10], rax.text:00000001400010E7 mov [rsp+38h+arg_18], rax.text:00000001400010EC call sub_140001080.text:00000001400010F1 lea rdx, [rsp+38h+arg_18].text:00000001400010F6 lea rcx, aI64d ; "%I64d".text:00000001400010FD call sub_140001080.text:0000000140001102 mov rcx, [rsp+38h+arg_18] .text:0000000140001107 mov rax, 5555555555555556h.text:0000000140001111 imul [rsp+38h+arg_10].text:0000000140001116 mov rax, 6666666666666667h.text:0000000140001120 mov r10, rdx.text:0000000140001123 shr r10, 3Fh.text:0000000140001127 add r10, rdx.text:000000014000112A imul rcx.text:000000014000112D mov [rsp+38h+var_18], r10.text:0000000140001132 mov r9, rdx.text:0000000140001135 sar r9, 1.text:0000000140001138 mov rax, r9.text:000000014000113B shr rax, 3Fh.text:000000014000113F add r9, rax .text:0000000140001142 mov rax, 2AAAAAAAAAAAAAABh.text:000000014000114C imul rcx.text:000000014000114F mov rax, 1C71C71C71C71C72h.text:0000000140001159 mov r8, rdx.text:000000014000115C shr r8, 3Fh.text:0000000140001160 add r8, rdx.text:0000000140001163 imul rcx.text:0000000140001166 lea rcx, aI64dI64dLldLld ; "%I64d%I64d%lld%lld".text:000000014000116D mov rax, rdx.text:0000000140001170 shr rax, 3Fh.text:0000000140001174 add rdx, rax.text:0000000140001177 call sub_140001020.text:000000014000117C lea rcx, aPause ; "pause".text:0000000140001183 call sub_1400045C4.text:0000000140001188 xor eax, eax.text:000000014000118A add rsp, 38h.text:000000014000118E retnLooking at the disassembly, it is actually consistent with x86.
Here, we still remove pipeline optimization, extract the core code position for disassembly.
The M value increases, and we can substitute into the formula. Here, using mov r10, rdx indicates that rdx is being used directly, and rdx is a 64-bit number, so 2^64 / M = 2.9999999 rounded up = 3.
5.3 Linux GCC x86 Signed Non-Power-of-Two
Advanced code:
#include<stdio.h> int main(){ int NumberOne = 0; int NumberTwo = 0; scanf("%d", &NumberOne); scanf("%d", &NumberTwo); int Count1 = NumberOne / 3; int Count2 = NumberTwo / 5; int Count3 = NumberTwo / 6; int Count4 = NumberTwo / 9; printf("%d%d%d%d", Count4, Count3, Count2, Count1); scanf("%d", &Count4); scanf("%d", &Count3); scanf("%d", &Count2); scanf("%d", &Count1); printf("%d%d%d%d", Count4, Count3, Count2, Count1); return 0;}If you are on a 64-bit system, then use the gcc command as follows:
gcc xxx.c -o2 -m32Compile it, and actually the disassembly below is the same as x86 VC++6.0 vs2019, so it can be ignored.
Disassembly:
.text:080484BB ; int __cdecl main(int argc, const char **argv, const char **envp).text:080484BB public main.text:080484BB main proc near ; DATA XREF: _start+17↑o.text:080484BB.text:080484BB var_24 = dword ptr -24h.text:080484BB var_20 = dword ptr -20h.text:080484BB var_1C = dword ptr -1Ch.text:080484BB var_18 = dword ptr -18h.text:080484BB var_14 = dword ptr -14h.text:080484BB var_10 = dword ptr -10h.text:080484BB var_C = dword ptr -0Ch.text:080484BB argc = dword ptr 8.text:080484BB argv = dword ptr 0Ch.text:080484BB envp = dword ptr 10h.text:080484BB.text:080484BB ; __unwind {.text:080484BB lea ecx, [esp+4].text:080484BF and esp, 0FFFFFFF0h.text:080484C2 push dword ptr [ecx-4].text:080484C5 push ebp.text:080484C6 mov ebp, esp.text:080484C8 push ebx.text:080484C9 push ecx.text:080484CA sub esp, 20h.text:080484CD mov eax, large gs:14h.text:080484D3 mov [ebp+var_C], eax.text:080484D6 xor eax, eax.text:080484D8 mov [ebp+var_24], 0.text:080484DF mov [ebp+var_20], 0.text:080484E6 sub esp, 8.text:080484E9 lea eax, [ebp+var_24].text:080484EC push eax.text:080484ED push offset unk_80486B0.text:080484F2 call ___isoc99_scanf.text:080484F7 add esp, 10h.text:080484FA sub esp, 8.text:080484FD lea eax, [ebp+var_20].text:08048500 push eax.text:08048501 push offset unk_80486B0.text:08048506 call ___isoc99_scanf.text:0804850B add esp, 10h.text:0804850E mov ecx, [ebp+var_24] .text:08048511 mov edx, 55555556h.text:08048516 mov eax, ecx.text:08048518 imul edx.text:0804851A mov eax, ecx.text:0804851C sar eax, 1Fh.text:0804851F sub edx, eax.text:08048521 mov eax, edx.text:08048523 mov [ebp+var_1C], eax.text:08048526 mov ecx, [ebp+var_20] .text:08048529 mov edx, 66666667h.text:0804852E mov eax, ecx.text:08048530 imul edx.text:08048532 sar edx, 1.text:08048534 mov eax, ecx.text:08048536 sar eax, 1Fh.text:08048539 sub edx, eax.text:0804853B mov eax, edx.text:0804853D mov [ebp+var_18], eax.text:08048540 mov ecx, [ebp+var_20] .text:08048543 mov edx, 2AAAAAABh.text:08048548 mov eax, ecx.text:0804854A imul edx.text:0804854C mov eax, ecx.text:0804854E sar eax, 1Fh.text:08048551 sub edx, eax.text:08048553 mov eax, edx.text:08048555 mov [ebp+var_14], eax.text:08048558 mov ecx, [ebp+var_20] .text:0804855B mov edx, 38E38E39h.text:08048560 mov eax, ecx.text:08048562 imul edx.text:08048564 sar edx, 1.text:08048566 mov eax, ecx.text:08048568 sar eax, 1Fh.text:0804856B sub edx, eax.text:0804856D mov eax, edx5.4 Other Similar Projects for Research
Establish your own projects for research, experts review, and beginners learn. Thank you for watching.
– End –
Kanxue ID: TkBinary
https://bbs.pediy.com/user-home-723188.htm
* This article is original by Kanxue Forum TkBinary, please indicate the source from Kanxue Community when reprinting.
Limited quantity of 25% discount tickets, first come first served!
Recommended Articles++++
* Things to Learn about Minifilter
* A New Upload of KimSuky Old Sample Analysis
* Three Ways to Write the Character “Hui” in Angr Symbolic Execution to Find Flag
* Introduction to stdin in IO-FILE
* Restoration of Disassembled Code for Power-of-Two Divisors
Official WeChat ID: ikanxueOfficial Weibo: Kanxue SecurityBusiness Cooperation: [email protected]
Please Share
Please Like
Please Read
Click “Read the Original Text” to recharge together!