Random signals cannot be represented by deterministic mathematical relationships and cannot predict their future instantaneous values. Any observation only represents one of the possible outcomes within its range of variation, and its value changes according to statistical laws. It is not a deterministic function of time, and there is no definite function value at any moment within its domain.Matlab provides various functions based on random signal processing, and this article introduces the rand() function.The rand() function is used to generate pseudo-random numbers uniformly distributed in the interval [0,1).
Generating a single random number
r = rand(); % Generate a random number between 0 and 1When no input parameters are provided, it returns a single double-precision floating-point random number.
Generating matrices or higher-dimensional arrays
Specify dimensions: By inputting parameters such as the number of rows (m) and columns (n), you can generate multi-dimensional arrays:
A = rand(3,4); % Generate a 3×4 random matrixB = rand(2,3,2); % Generate a 2×3×2 three-dimensional random array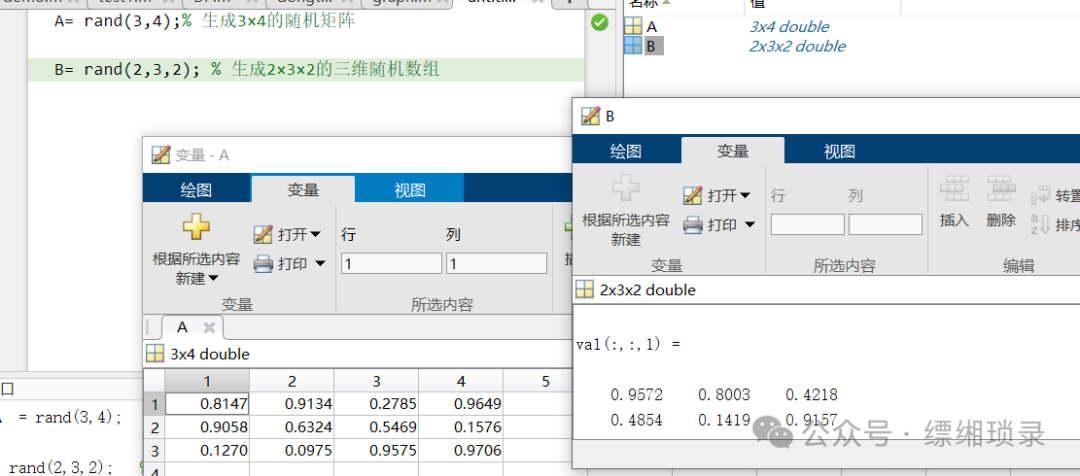
Matching existing matrix dimensions
Use rand(size(X)) to generate a random array with the same dimensions as matrix X.
Generating specific types of random numbers
Specify the data type using the CLASSNAME parameter, for example, to generate single-precision floating-point numbers:
C = rand(3, 'single'); % Generate a 3×3 single-precision random matrix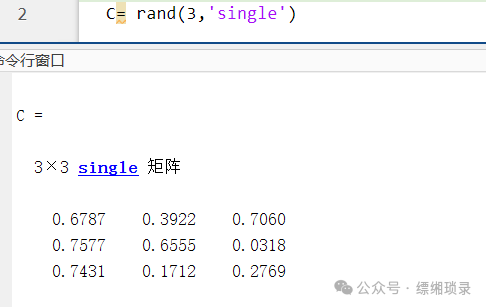
Setting the random number seed
To ensure reproducibility of experiments, the initial state of the random number generator must be fixed. In older versions, the seed can be set using rand(‘state’, s) (where s is an integer), but in newer versions, it is recommended to use rng(s).
rng(42); % Set the seed to 42D = rand(2,2); % Generate the same random matrix each time
Dynamically adjusting dimensions
Input parameters can be scalars or vectors, for example:
E = rand([3,4]); % Equivalent to rand(3,4)Application tips
Generating random numbers within a specific range
Adjust the range of random numbers through linear transformation:
Generating numbers in the interval [a, b)
a + (b - a) * rand();Generating integer combinations
Using floor or round functions, for example, generating integers from 1 to 10:
num = floor(1 + 10 * rand()); % Generate an integer from 1 to 10 by flooringNotes
rand() generates pseudo-random numbers based on a deterministic algorithm. If the seed is not set, it defaults to initializing based on the system time, which may lead to inconsistent results across different runs.
When generating high-dimensional arrays, it is preferable to use vector parameters (e.g., rand([m,n,p])) rather than continuous inputs (e.g., rand(m,n,p)) to reduce memory overhead.
rand(n) generates an n×n matrix, not n random numbers.
Parameters must be integers; otherwise, an error will occur.
Example code
Generating a random matrix from 10 to 20
random_matrix = 10 + 10 * rand(3); % 3×3 matrix, elements range [10,20)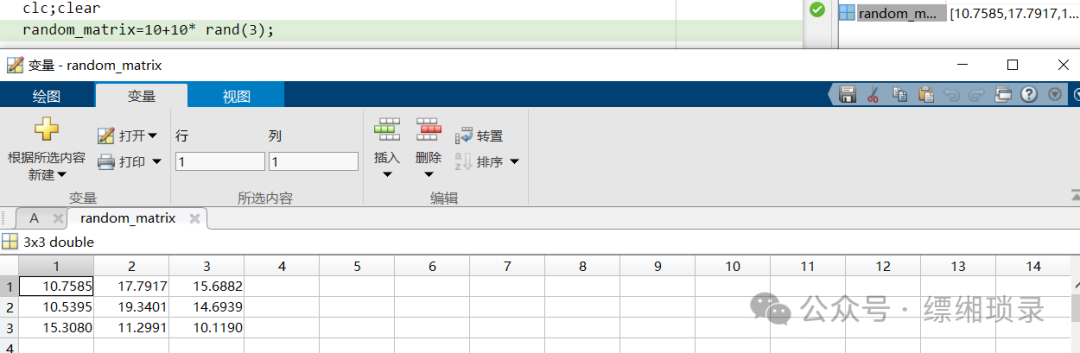
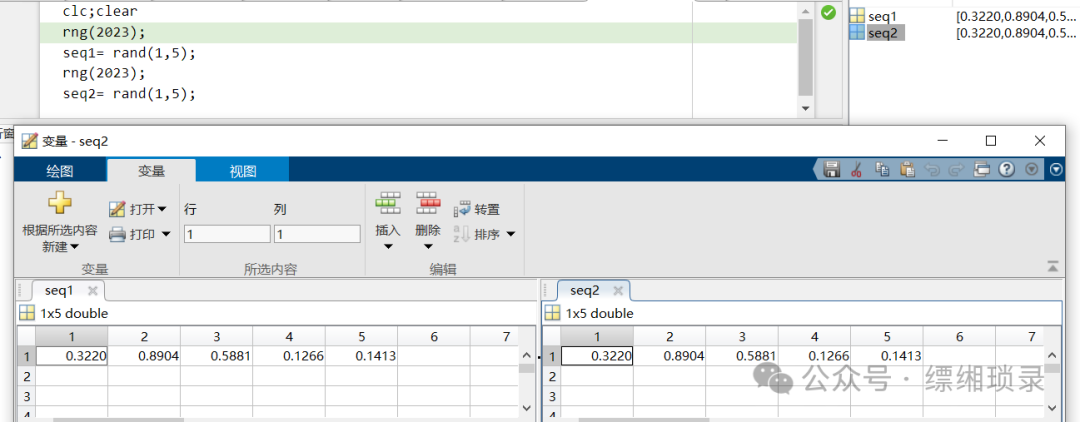
Reproducing random sequences
rng(2023); % Fix the seedseq1 = rand(1,5);rng(2023); % Reset the seedseq2 = rand(1,5); % seq1 and seq2 are identical