01 Program Structure Optimization
1. Program Writing Structure Although the writing format does not affect the quality of the generated code, certain writing rules should still be followed during actual programming. A clearly written program is beneficial for future maintenance. When writing programs, especially for statements like While, for, do…while, if…else, switch…case, and their nested combinations, a “structured” writing format should be adopted.
2. Identifiers User-defined identifiers in the program should not only follow naming conventions but also avoid using algebraic symbols (like a, b, x1, y1) as variable names. Instead, choose meaningful English words (or abbreviations) or Pinyin to enhance program readability, such as: count, number1, red, work, etc.3. Program Structure C language is a high-level programming language that provides a complete set of standardized control structures. Therefore, when designing microcontroller application system programs in C, it is essential to adopt a structured programming approach as much as possible. This makes the entire application system program structure clear and facilitates debugging and maintenance.
For a larger application program, the entire program is usually divided into several modules based on functionality, with different modules performing different functions. Each module can be written separately, and even by different programmers. Generally, the functionality of a single module is relatively simple, making design and debugging easier. In C language, a function can be considered a module.
Modular programming not only involves dividing the entire program into several functional modules but also emphasizes maintaining the relative independence of variables between modules, i.e., keeping modules independent and minimizing the use of global variables. Commonly used functional modules can also be encapsulated into an application library for direct invocation when needed. However, if modules are divided too finely, it may lead to reduced execution efficiency (the time taken to save and restore registers when entering and exiting a function).
4. Defining Constants During program design, for frequently used constants, if they are directly written into the program, any change in their values will require finding and modifying each instance in the program, which inevitably reduces maintainability. Therefore, it is advisable to define constants using preprocessor commands to avoid input errors.5. Reducing Conditional Statements Use conditional compilation (ifdef) wherever possible instead of if statements, which helps reduce the length of the generated code.6. Expressions For expressions where the order of operations is unclear or easily confused, parentheses should be used to explicitly specify their precedence. An expression should not be overly complex; if it is too complicated, it will be difficult to understand later, hindering future maintenance.7. Functions For functions in the program, the type of the function should be specified before use, ensuring it matches the originally defined function type. Functions with no parameters and no return type should be marked with “void”. If code length needs to be shortened, common code segments can be defined as functions. If execution time needs to be reduced, some functions can be replaced with macros after debugging is complete. Note that macros should only be defined after debugging, as most compilers report errors only after macro expansion, complicating error detection.8. Minimize Global Variables, Use Local Variables More Global variables are stored in data memory; defining a global variable reduces the available data memory space for the MCU. If too many global variables are defined, the compiler may not have enough memory to allocate. Local variables, on the other hand, are mostly located in the internal registers of the MCU. In most MCUs, using register operations is faster than using data memory, and the instructions are more flexible, leading to higher quality code generation. Additionally, the registers and data memory occupied by local variables can be reused across different modules.9. Set Appropriate Compiler Options Many compilers have different optimization options. Before use, one should understand the meaning of each optimization option and choose the most suitable one. Generally, once the highest level of optimization is selected, the compiler may excessively pursue code optimization, potentially affecting program correctness and causing runtime errors. Therefore, it is essential to be familiar with the compiler being used and know which parameters are affected by optimization and which are not. 02 Code Optimization
1. Choose Appropriate Algorithms and Data Structures Familiarity with algorithm languages is essential. Replace slower sequential search methods with faster binary search or unordered search methods, and replace insertion sort or bubble sort with quick sort, merge sort, or heap sort to significantly improve program execution efficiency.
Choosing an appropriate data structure is also crucial. For example, using a lot of insert and delete instructions in a randomly stored dataset is much faster than using a linked list. Arrays and pointers are closely related; generally, pointers are more flexible and concise, while arrays are more intuitive and easier to understand. For most compilers, using pointers generates shorter code and higher execution efficiency than using arrays.
However, in Keil, the opposite is true; using arrays generates shorter code than using pointers.
2. Use the Smallest Data Types Possible If a character type (char) variable can be used, do not use an integer (int) variable; if an integer variable can be used, do not use a long integer (long int); and if a floating-point (float) variable can be avoided, do not use it. Of course, after defining a variable, do not exceed its scope. If a value is assigned beyond the variable’s range, the C compiler will not report an error, but the program’s runtime result will be incorrect, and such errors are difficult to detect.
3. Use Increment and Decrement Instructions Typically, using increment and decrement instructions and compound assignment expressions (like a-=1 and a+=1) can generate high-quality program code. Compilers usually generate instructions like inc and dec, while using a=a+1 or a=a-1 often results in 2-3 bytes of instructions from many C compilers.
4. Reduce Computational Intensity Replace complex expressions with simpler expressions that perform the same function. For example:(1) Modulus Operation
a=a%8;
can be changed to: a=a&7;
Explanation: Bitwise operations can be completed in one instruction cycle, while most C compilers call a subroutine to perform the “%” operation, resulting in longer code and slower execution. Generally, for modulus of 2^n, bitwise operations can be used instead.
(2) Square Operationa=pow(a,2.0); can be changed to: a=a*a; Explanation: In microcontrollers with built-in hardware multipliers (like the 51 series), multiplication is much faster than calculating squares, as floating-point square calculations are implemented through subroutine calls. In AVR microcontrollers with built-in hardware multipliers, like ATMega163, multiplication can be completed in just 2 clock cycles. Even in AVR microcontrollers without built-in hardware multipliers, the subroutine for multiplication is shorter and faster than that for square calculations. If calculating cubes, for example:a=pow(a,3.0); can be changed to: a=a*a*a; the efficiency improvement is even more significant.(3) Use Shifts for Multiplication and Divisiona=a*4;b=b/4; can be changed to: a=a<<2;b=b>>2; Explanation: Generally, if multiplication or division by 2^n is needed, shifts can be used instead. In ICCAVR, multiplying by 2^n generates left shift code, while multiplying by other integers or dividing by any number calls multiplication/division subroutines. Using shifts results in more efficient code than calling multiplication/division subroutines. In fact, any multiplication or division by an integer can be achieved using shifts, such as:a=a*9 can be changed to: a=(a<<3)+a
5. Loops
(1) Loop Statements For tasks that do not require the loop variable to participate in calculations, they can be placed outside the loop. These tasks include expressions, function calls, pointer operations, array accesses, etc. All unnecessary operations should be grouped together and placed in an init initialization program.
(2) Delay Functions Commonly used delay functions typically use increment forms:
void delay (void){unsigned int i;for (i=0;i<1000;i++); }Change it to a decrement delay function: void delay (void){unsigned int i;for (i=1000;i>0;i–); } The delay effect of both functions is similar, but almost all C compilers generate 1-3 bytes less code for the latter function because almost all MCUs have instructions for zero transfer, and using the latter method can generate such instructions. The same applies when using while loops; using decrement instructions to control the loop generates 1-3 bytes less code than using increment instructions. However, when there are instructions in the loop that read and write arrays using the loop variable “i”, using pre-decrement loops may cause array out-of-bounds issues, which should be noted.(3) While Loops and Do…While Loops There are two forms of while loops:
unsigned int i;i=0;while (i<1000){i++; // User program} or: unsigned int i;i=1000;do{i--; // User program}while (i>0);In these two loops, the code generated by the do…while loop is shorter than that of the while loop after compilation.
6. Lookup Tables In programs, avoid performing very complex calculations, such as floating-point multiplication, division, and square roots, as well as complex mathematical model interpolation calculations. For these time-consuming and resource-consuming operations, it is advisable to use lookup tables and place the data tables in program storage. If generating the required table directly is difficult, it is better to calculate it at startup and then generate the required table in data memory, allowing direct lookup during program execution, thus reducing the workload of repeated calculations during execution.
7. Others
For example, using inline assembly and storing strings and constants in program memory are beneficial for optimization. 03 Multiplication and Division Optimization
Currently, the competition in the microcontroller market is fierce. Many applications choose to use small resource 8-bit MCU chips with smaller program storage space (like 1K, 2K) for cost-effectiveness. Generally, these MCUs do not have hardware multiplication and division instructions. When multiplication and division operations are necessary, relying solely on the compiler to call internal function libraries often results in large code size and low execution efficiency.
Shanghai Shengxi Microelectronics has launched the MC30 and MC32 series MCUs, which adopt RISC architecture and have a large user base and wide applications in the small resource 8-bit MCU field. This article uses the instruction sets of these two series of products from Shengxi Microelectronics as examples, combined with assembly and C compilation platforms, to introduce a time-saving and resource-saving multiplication and division algorithm.
1. Multiplication Section Multiplication in microcontrollers is binary multiplication, which involves multiplying each bit of the multiplier with the multiplicand and then summing them up. Since both the multiplier and multiplicand are binary, each multiplication step can be implemented using shifts.
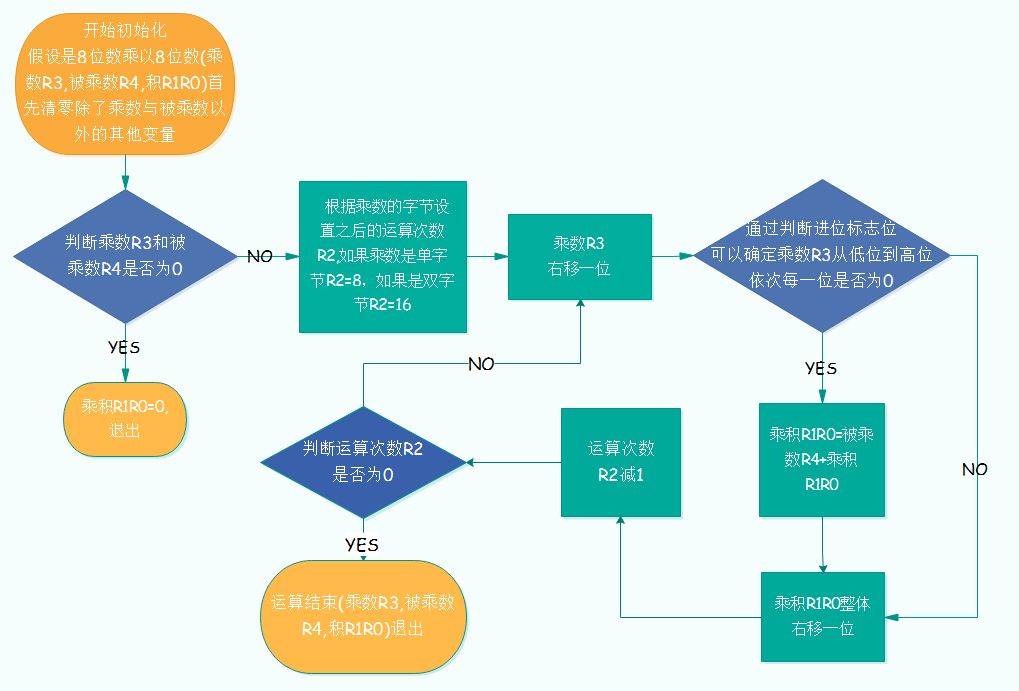
For example: Multiplier R3=01101101, multiplicand R4=11000101, product R1R0. The steps are as follows:
1. Clear the product R1R0;
2. The 0th bit of the multiplier is 1, so the multiplicand R4 needs to be multiplied by binary 1, which means left shifting by 0 bits and adding to R1R0;
3. The 1st bit of the multiplier is 0, ignore;
4. The 2nd bit of the multiplier is 1, so the multiplicand R4 needs to be multiplied by binary 100, which means left shifting by 2 bits and adding to R1R0;
5. The 3rd bit of the multiplier is 1, so the multiplicand R4 needs to be multiplied by binary 1000, which means left shifting by 3 bits and adding to R1R0;
6. The 4th bit of the multiplier is 0, ignore;
7. The 5th bit of the multiplier is 1, so the multiplicand R4 needs to be multiplied by binary 100000, which means left shifting by 5 bits and adding to R1R0;
8. The 6th bit of the multiplier is 1, so the multiplicand R4 needs to be multiplied by binary 1000000, which means left shifting by 6 bits and adding to R1R0;
9. The 7th bit of the multiplier is 0, ignore;
10. At this point, the value in R1R0 is the final product, and the algorithm is complete.
The result of the above example:
R1R0 = R3 * R4= (R4<<6)+(R4<<5)+(R4<<3)+(R4<<2)+R4 = 101001111100001
The actual operation flowchart is shown below:
In actual program design, program optimization has two goals: improving program execution efficiency and reducing code size. Let’s look at the efficiency and code size comparison between the assembly algorithm provided in this article and ordinary C programming.
Table 1.1 shows the comparison data for program execution efficiency (there may be slight deviations). It is evident that the execution time compiled from assembly is significantly less than that from C language.
|
|
|
|
|
|
|
|
|
|
|
|
Table 1.1 Multiplication Operation Clock Cycle Comparison Table Table 1.2 shows the comparison data for program code size (there may be slight deviations). Assembly occupies much less program space than C language.
|
|
|
|
|
|
|
|
|
|
|
|
Table 1.2 Multiplication Operation ROM Space Usage Comparison Table In summary, the multiplication algorithm introduced in this article performs significantly better than C compilation in all aspects. If you encounter issues where the existing program does not meet application requirements, such as insufficient program space or excessive runtime, you can optimize it using the methods outlined above. Assembly language is the closest to machine language. In assembly language, you can directly manipulate registers and adjust the execution order of instructions. Since assembly language directly interfaces with the hardware platform, and different hardware platforms have significant differences in instruction sets and cycles, this can cause some inconvenience in program portability and maintenance. Therefore, we have provided multiplication operation examples for the reduced instruction set to facilitate portability and understanding.
2. Division Section Division in microcontrollers is also binary division, similar to mathematical division in reality. It starts from the high bit of the dividend, performing bitwise division by the divisor and taking the remainder, which is then combined with the subsequent dividend for new division until it cannot be divided anymore. Since division in microcontrollers is binary, the quotient at each step can only be 1. For example: Dividend R3R4=1100110001101101, divisor R5=11000101, quotient R1R0, remainder R2. The steps are as follows:1. Clear the quotient R1R0 and remainder R2;2. Release the highest bit of the dividend, the 15th bit, which is 1. 1 is less than the divisor, so the quotient is 0, and the remainder R2 is 1;3. The previous remainder combined with the next highest bit of the dividend, the 14th bit, gives 11, which is still less than the divisor, so the quotient is 0, and the remainder R2 is 11;4. Until the 8th bit is released, giving 11001100, which is greater than the divisor, the quotient is 1, and the remainder R2 is 111;5. The previous remainder combined with the 7th bit of the dividend gives 1110, which is not greater than the divisor, so the quotient is 0, and the remainder R2 is 1110;6. The previous remainder combined with the 6th bit of the dividend gives 11101, which is not greater than the divisor, so the quotient is 0, and the remainder R2 is 11101;7. Following the above steps, until the 3rd bit of the dividend is released, giving 11101101, which is greater than the divisor, the quotient is 1, and the remainder R2 is 101000;8. The previous remainder combined with the 2nd bit of the dividend gives 1010001, which is not greater than the divisor, so the quotient is 0, and the remainder R2 is 1010001;9. The previous remainder combined with the 1st bit of the dividend gives 10100010, which is not greater than the divisor, so the quotient is 0, and the remainder R2 is 10100010;10. The previous remainder combined with the 0th bit of the dividend gives 101000101, which is greater than the divisor, so the quotient is 1, and the remainder R2 is 10000000;11. Finally, the quotients obtained from all the above steps are arranged from left to right to form the final quotient 100001001, with the remainder being the last calculated remainder 10000000. The result of the above example: R1R0 = R3R4 / R5 = 100001001; R2 = R3R4 % R5 = 10000000 The actual operation flowchart is shown below: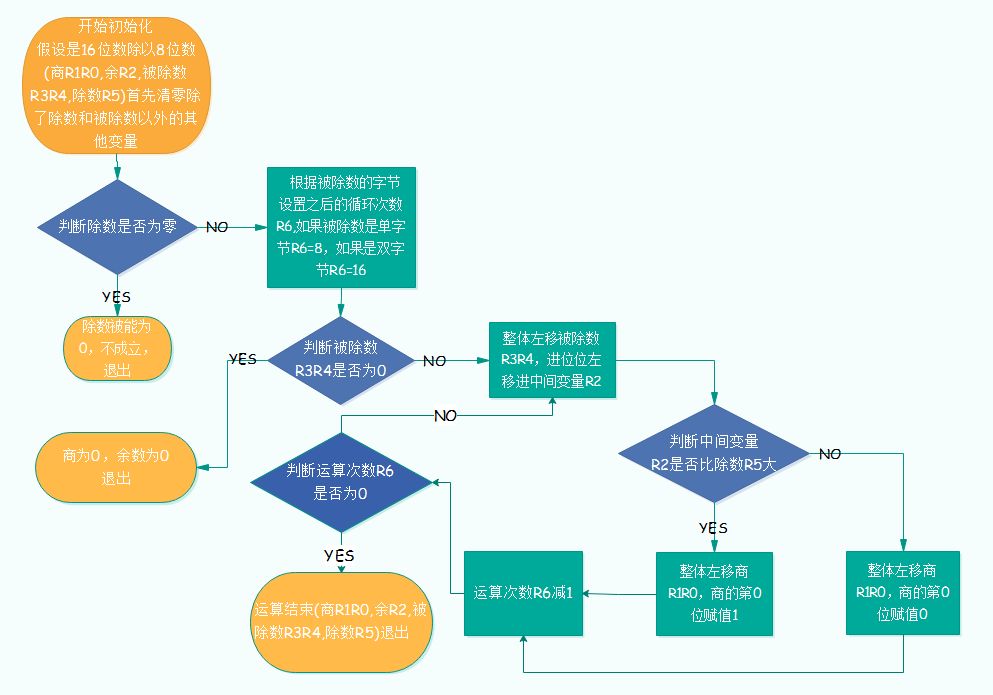
The efficiency and code size of division operations are shown in the following table. Table 2.1 shows the comparison data for program execution efficiency and code size (there may be slight deviations). It is evident that the assembly algorithm provided in this article is much more optimized.
|
|
|
|
|
|
|
|
|
Table 2.1 Division Operation Clock Cycle Comparison Table Therefore, the method provided in this article for division operations is also relatively optimal. Below is an example of division operations for the reduced instruction set, specifically for 16/8 bit, to facilitate portability and understanding.
Recommended Reading
Click the image to read
Can the feedback resistors of the DCDC divider be chosen arbitrarily?
Which PCB design do you like from the electronic genius’s creative designs?
Stop buying development boards! Check out this hardware microcontroller simulator.