Detailed Explanation of AES Encryption Algorithm Principles

Source: https://www.biaodianfu.com/aes.html

The Data Encryption Standard (DES) has a key length of 56 bits, resulting in a theoretical security strength of 256. However, the late 20th century was a period of rapid development in computing, and advancements in component manufacturing technology led to increasing computational power, making DES insufficiently secure. On January 2, 1997, the National Institute of Standards and Technology (NIST) in the United States announced a call for the Advanced Encryption Standard (AES) to replace DES. The requirements for AES were:

• NIST proposed several hard requirements during the algorithm solicitation:

• Block cipher algorithm: supports a block size of 128 bits and key lengths of 128/192/256 bits

• Security not lower than 3DES, but implementation and execution must be more efficient than 3DES

• Optimized ANSI C implementation code

• KAT (Known-Answer Tests) and MCT (Monte Carlo Tests) for testing and validation

• Convenience for both software and hardware implementation

• Resistance to known attacks

AES received responses from many cryptographers worldwide, and many individuals submitted their designed algorithms. In the first round, a total of 15 algorithms were shortlisted, with 5 algorithms reaching the finals: Rijndael, Serpent, Twofish, RC6, and MARS. After three years of validation, evaluation, and public discussion, the Rijndael algorithm was ultimately selected. Rijndael is a family of block cipher algorithms proposed by Belgian scholars Joan Daemen and Vincent Rijmen, with the algorithm’s name derived from the combination of the two authors’ names. Its block lengths include 128 bits, 160 bits, 192 bits, 224 bits, and 256 bits, and key lengths also include these five lengths, but ultimately AES selected three versions with a block length of 128 bits and key lengths of 128 bits, 192 bits, and 256 bits.

The advantages of Rijndael lie in its integration of security, performance, efficiency, implementability, and flexibility. The design philosophy of Rijndael includes:

• Security: The algorithm is sufficiently strong to resist attacks

• Efficiency: The algorithm has high computational efficiency

• Key Agility: Minimal loss when changing keys, i.e., a minimally consuming key expansion algorithm

• Versatility: Suitable for implementation on different CPU architectures, software, or hardware platforms

• Simplicity: The design of the round function is streamlined, consisting of multiple iterations

Algorithm Principles of AES

General design principles of encryption algorithms

• Confusion: Maximize the complexity of the relationship between ciphertext, plaintext, and keys, typically achieved through nonlinear transformation algorithms for maximum confusion.

• Diffusion: Each change in the plaintext or key should maximally affect the bits in the ciphertext, usually achieved through linear transformation algorithms for maximum diffusion.

For the Rijndael algorithm, the decryption process is the reverse of the encryption process. The diagram below illustrates the AES encryption and decryption process, showing that: 1) Each step of the decryption algorithm corresponds to the inverse operation of the encryption algorithm, and 2) The order of all operations in encryption and decryption is precisely reversed. These points, along with the inverse operations of each step of the encryption and decryption algorithms, ensure the correctness of the algorithm.

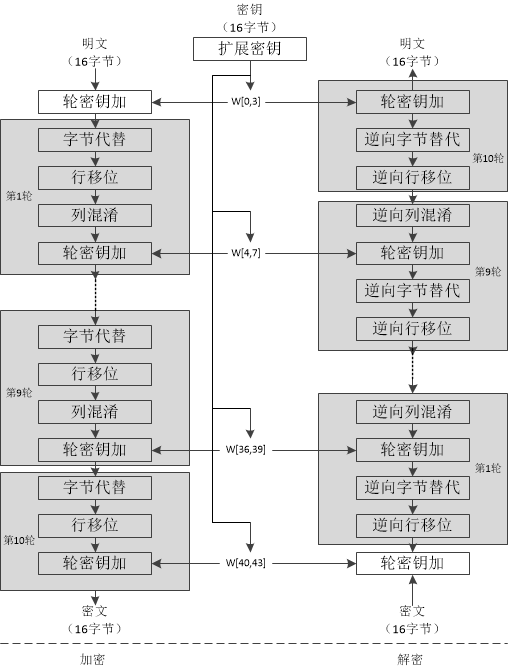
The Rijndael algorithm is an iterative algorithm based on a substitution-permutation network (SPN). Plaintext data is transformed through multiple rounds to generate ciphertext, with each round’s transformation defined by the round function.

• The left side of the diagram shows the process of the round function, which mainly includes four primary operations: SubByte, ShiftRow, MixColumn, and AddRoundKey.

• The right side of the diagram shows the key schedule scheme, known as the key expansion algorithm in Rijndael.

Round Function

We have established that the round function primarily consists of four operations, but the specific operations performed by different rounds are not the same. The main distinction is between the initial round (Round: 0) and the final round (Round: Nr), while all intermediate rounds perform the same operations in sequence, namely:

• SubByte

• ShiftRow

• MixColumn

• AddRoundKey

The Rijndael algorithm supports plaintext blocks larger than 128 bits, requiring a matrix with more columns to describe. The operations of the Rijndael round function are performed over a specially defined finite field GF(256). A finite field, also known as a Galois field, is simply a set that satisfies specific rules, where the elements can perform addition, subtraction, multiplication, and division, and the results also belong to this set. According to the definition of Rijndael, the number of encryption rounds will vary based on different block sizes and key lengths:

The AES standard only supports a block size of 128 bits (Nb = 4). The AES standard algorithm generates a 4×4 matrix from the 128-bit plaintext, in a specific order (each element is one byte, 8 bits), known as the initial state, which, after undergoing iterative transformations through the round function, will serve as input for the next round until the iterations conclude.

Round Function Breakdown: Substitute Bytes

The Substitute Bytes operation (SubBytes) replaces each independent element in the state matrix by looking it up in the substitution box (S-box). This operation is a reversible nonlinear transformation and the only nonlinear transformation in the AES operation group. The inverse operation of Substitute Bytes is also completed through reverse lookups and replacements in the S-box, primarily mapping one byte to another.

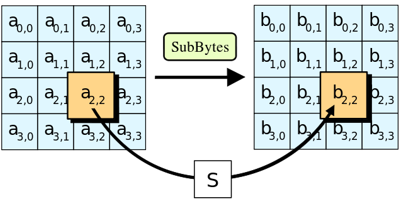
The S-box is constructed from the multiplication inverse in the finite field GF(256) followed by a linear affine transformation; it is not a simple lookup table constructed arbitrarily. Due to the complexity of the S-box operation, many AES software and hardware implementations directly use lookup tables (LUT, Look-up table), but this method may not be suitable for all scenarios. For specific hardware designs minimizing area, optimized combinational logic is used to achieve equivalent S-box replacements. The S-box is a pre-designed 16×16 lookup table, containing 256 elements. The S-box provides confusion in the cryptographic algorithm. The detailed construction method of the S-box can be referenced in the literature. Here, we directly present the constructed results, where figure (a) is the S-box, and figure (b) is S-1 (the inverse of the S-box). S and S-1 are both 16×16 matrices that complete a mapping from 8-bit input to 8-bit output, where the high 4 bits of the input correspond to the row index, and the low 4 bits correspond to the column index.

Round Function Breakdown: Shift Rows

The purpose of Shift Rows is to achieve diffusion of bytes within each row, which is a linear transformation. Shift Rows is a permutation of the bytes within a 4×4 matrix that provides diffusion for the algorithm.

1) Forward Shift Rows

Forward Shift Rows is used during encryption, as shown in the diagram below. In this case, the first row remains unchanged, the second row is cyclically left shifted by 8 bits, the third row by 16 bits, and the fourth row by 24 bits. Assuming the matrix is named state, it can be expressed by the formula: state’[i][j] = state[i][(j+i)%4]; where i, j belong to [0,3].

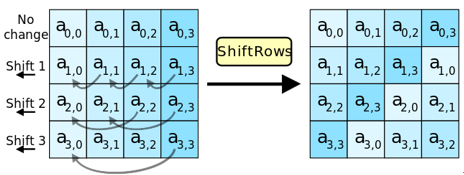
2) Inverse Shift Rows

Inverse Shift Rows is the reverse operation, where the first row remains unchanged, the second row is cyclically right shifted by 8 bits, the third row by 16 bits, and the fourth row by 24 bits. This can be expressed by the formula: state’[i][j] = state[i][(4+j-i)%4]; where i, j belong to [0,3].

Round Function Breakdown: Mix Columns

Mix Columns achieves diffusion in the columns by multiplying the state matrix with a constant matrix C, which is a substitution transformation. Mix Columns is the most complex step in the Rijndael algorithm, essentially involving polynomial multiplication in the finite field GF(256).

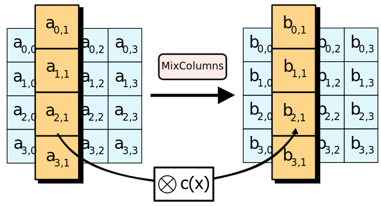
1) Forward Mix Columns

The diagram for Forward Mix Columns is shown below:

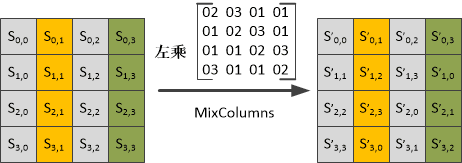
According to matrix multiplication, during the column mixing process, each byte’s corresponding value only relates to the four values in that column. Note the following points regarding multiplication and addition defined over GF(28):

• Multiplying a byte’s corresponding value by 2 results in left-shifting the binary value by one position; if the original value’s highest bit is 1, the result after shifting must be XORed with 00011011;

• Multiplication distributes over addition, e.g., 07·S0,0=(01⊕02⊕04)·S0,0= S0,0⊕(02·S0,0)(04·S0,0)

• The matrix multiplication here differs from general matrix multiplication, as the values are combined using modulo 28 addition (XOR operation).

Below is an example, assuming the values of a certain column are shown in the diagram, with the computation process illustrated:

When calculating the product of 02 and C9, since C9’s leftmost bit is 1, the value obtained by left-shifting C9 must be XORed with (0001 1011). The same calculation can be performed for the other values.

2) Inverse Mix Columns

The diagram for Inverse Mix Columns is shown below:

Since:

This indicates that the two matrices are inverses of each other, and after one inverse column mixing, the original text can be restored.

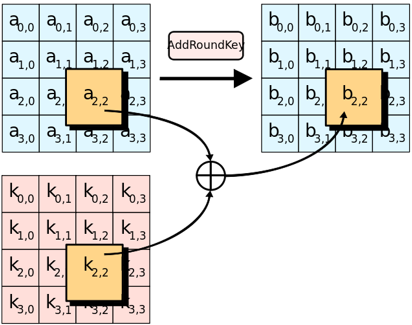
Round Function Breakdown: Add Round Key

Add Round Key is a simple operation where the round key is XORed bit by bit with the state. This operation is relatively straightforward, based on the principle that “any number XORed with itself results in 0.” During the encryption process, the input of each round is XORed with the round key; therefore, during decryption, XORing again with the same round key restores the original.

Key Expansion Algorithm

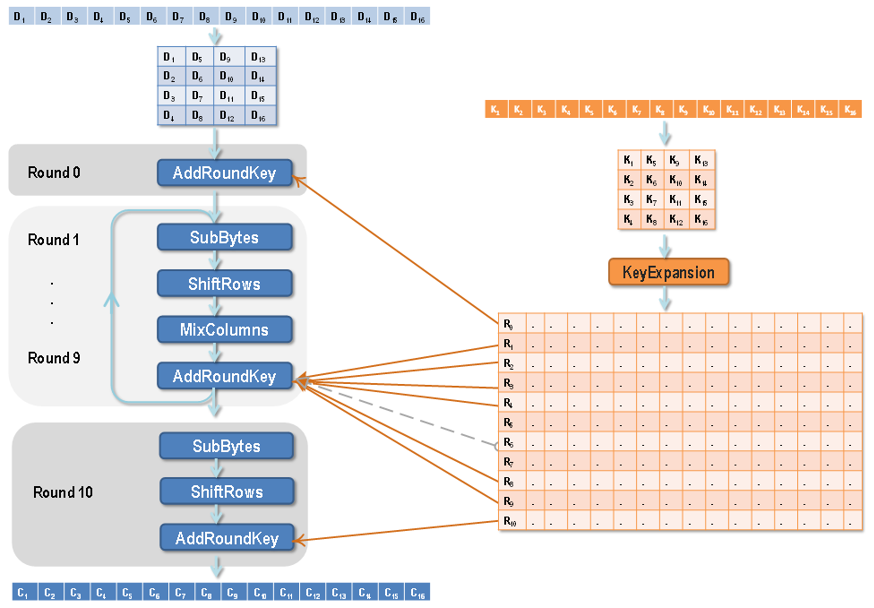
In AES encryption and decryption, the keys for each round are derived from the seed key through the key expansion algorithm. The 16-byte plaintext, ciphertext, and round keys are all represented as a 4×4 matrix.

The key expansion algorithm is the implementation algorithm for Rijndael’s key schedule, aimed at generating multiple round keys from the seed key (user key). The round keys consist of multiple 128-bit keys, corresponding to different key lengths of 11, 13, and 15 groups.

The diagram for the key expansion process is shown below:

Key expansion process explanation:

1) Arrange the seed key according to the format in diagram (a), where k0, k1, …, k15 represent each byte of the seed key; after arrangement, use four 32-bit words, denoted as w[0], w[1], w[2], w[3];

2) Solve w[j] in sequence, where j is an integer belonging to [4,43];

3) If j%4=0, then w[j]=w[j-4]⊕g(w[j-1]), otherwise w[j]=w[j-4]⊕w[j-1];

The process of function g is explained as follows:

1. a) Left rotate w by 8 bits;

2. b) Perform S-box substitution on each byte;

3. c) XOR with a 32-bit constant (RC[j/4],0,0,0); RC is a one-dimensional array with the following values. (Only 10 values of RC are needed, but here 11 are used; in fact, RC[0] is not used in the computation, and adding RC[0] is for convenience in representing it in an array. Since the minimum value of j is 4, the minimum value of j/4 is 1, so there will be no errors.)

RC = {0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36}

Animation demonstrating the encryption process:

• Enrique Zabala created an animation demonstrating the AES-128 encryption algorithm, clearly and intuitively introducing the execution process of the round function.

• Howard Straubing from Boston University created an animation to showcase the AES encryption algorithm.