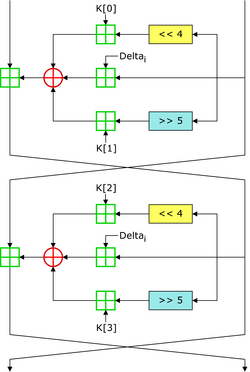
Implementation and Reverse Analysis of Tiny Encryption Algorithm

Implementation and Reverse Analysis of Tiny Encryption Algorithm
This article is a featured post from the KX forum.
KX forum Author ID: 丿feng
This article mainly provides a simple analysis of the TEA series algorithms, originally written by myself. If there are any infringements regarding the images and some code quoted in the text, please contact me.
>>>>

1. About TEA Series Algorithms

The Tiny Encryption Algorithm (TEA) is a block cipher that is easy to describe and implement, requiring very little code. Its designers are David Wheeler and Roger Needham.
TEA has a block length of 64 bits and a key length of 128 bits, using a Feistel network, and it is recommended to perform 32 rounds of encryption, which amounts to 64 rounds.
XTEA is an extension of TEA, also a 64-bit block Feistel cipher, using a 128-bit key, and it is recommended to perform 64 rounds.
XXTEA is an unbalanced Feistel network block cipher that operates on variable-length blocks, which are multiples of 32 bits (minimum 64 bits), using a 128-bit key.
The characteristic feature of the TEA series algorithms is the use of the key scheduling constant 0x9e3779b9.
>>>>

2. Implementation of Encryption and Decryption

1. TEA Encryption and Decryption Implementation

Implementation and Reverse Analysis of Tiny Encryption Algorithm
#include <stdio.h>
void encrypt(unsigned int* v, unsigned int* key) {
 unsigned int l = v[0], r = v[1], sum = 0, delta = 0x9e3779b9;
 for (size_t i = 0; i < 32; i++) {
 sum += delta;
 l += ((r << 4) + key[0]) ^ (r + sum) ^ ((r >> 5) + key[1]);
 r += ((l << 4) + key[2]) ^ (l + sum) ^ ((l >> 5) + key[3]);
 }
 v[0] = l;
 v[1] = r;
}
 
void decrypt(unsigned int* v, unsigned int* key) {
 unsigned int l = v[0], r = v[1], sum = 0, delta = 0x9e3779b9;
 sum = delta *32;
 for (size_t i = 0; i < 32; i++) {
 r -= ((l << 4) + key[2]) ^ (l + sum) ^ ((l >> 5) + key[3]);
 l -= ((r << 4) + key[0]) ^ (r + sum) ^ ((r >> 5) + key[1]);
 sum -= delta;
 }
 v[0] = l;
 v[1] = r;
}
 
int main(int argc, char const *argv[])
{
 //test
 unsigned int v[2]={1,2},key[4]={1,2,3,4};
 printf("%u,%u\n",v[0],v[1]);
 encrypt(v,key);
 printf("%u,%u\n",v[0],v[1]);
 decrypt(v,key);
 printf("%u,%u\n",v[0],v[1]);
 return 0;
}

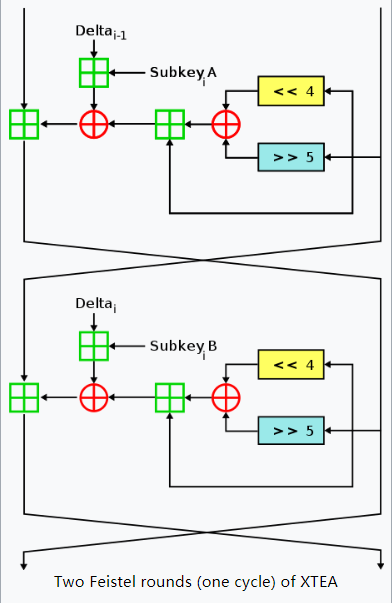
2. XTEA Encryption and Decryption Implementation

Implementation and Reverse Analysis of Tiny Encryption Algorithm
#include <stdio.h>
void encrypt(unsigned int* v, unsigned int* key) {
 unsigned int l = v[0], r = v[1], sum = 0, delta = 0x9e3779b9;
 for (size_t i = 0; i < 32; i++) {
 l += (((r << 4) ^ (r >> 5)) + r) ^ (sum + key[sum &amp; 3]);
 sum += delta;
 r += (((l << 4) ^ (l >> 5)) + l) ^ (sum + key[(sum >> 11) &amp; 3]);
 }
 v[0] = l;
 v[1] = r;
}
 
void decrypt(unsigned int* v, unsigned int* key) {
 unsigned int l = v[0], r = v[1], sum = 0, delta = 0x9e3779b9;
 sum = delta * 32;
 for (size_t i = 0; i < 32; i++) {
 r -= (((l << 4) ^ (l >> 5)) + l) ^ (sum + key[(sum >> 11) &amp; 3]);
 sum -= delta;
 l -= (((r << 4) ^ (r >> 5)) + r) ^ (sum + key[sum &amp; 3]);
 }
 v[0] = l;
 v[1] = r;
}
 
int main(int argc, char const *argv[])
{
 //test
 unsigned int v[2]={1,2},key[4]={1,2,3,4};
 printf("%u,%u\n",v[0],v[1]);
 encrypt(v,key);
 printf("%u,%u\n",v[0],v[1]);
 decrypt(v,key);
 printf("%u,%u\n",v[0],v[1]);
 return 0;
}

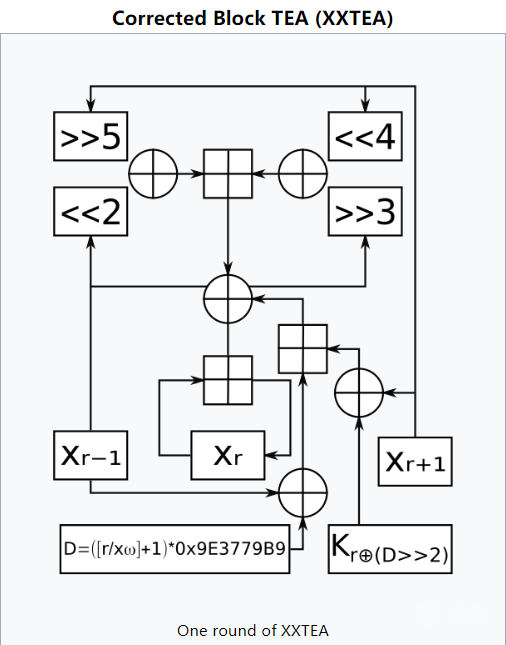
3. XXTEA Encryption and Decryption Implementation

Implementation and Reverse Analysis of Tiny Encryption Algorithm
#include <stdbool.h>
#include <stdio.h>
#define MX \
 ((z >> 5 ^ y << 2) + (y >> 3 ^ z << 4) ^ (sum ^ y) + (k[p &amp; 3 ^ e] ^ z))
bool btea(unsigned int* v, int n, unsigned int* k) {
 unsigned int z = v[n - 1], y = v[0], sum = 0, e, DELTA = 0x9e3779b9;
 unsigned int p, q;
 if (n > 1) { /* Coding Part */
 q = 6 + 52 / n;
 while (q-- > 0) {
 sum += DELTA;
 e = (sum >> 2) &amp; 3;
 for (p = 0; p < n - 1; p++)
 y = v[p + 1], z = v[p] += MX;
 y = v[0];
 z = v[n - 1] += MX;
 }
 return 0;
 } else if (n < -1) { /* Decoding Part */
 n = -n;
 q = 6 + 52 / n;
 sum = q * DELTA;
 while (sum != 0) {
 e = (sum >> 2) &amp; 3;
 for (p = n - 1; p > 0; p--)
 z = v[p - 1], y = v[p] -= MX;
 z = v[n - 1];
 y = v[0] -= MX;
 sum -= DELTA;
 }
 return 0;
 }
 return 1;
}
 
int main(int argc, char const* argv[]) {
 // test
 unsigned int v[2] = {1, 2}, key[4] = {1, 2, 3, 4};
 printf("%u,%u\n", v[0], v[1]);
 btea(v, 2, key);
 printf("%u,%u\n", v[0], v[1]);
 btea(v, -2, key);
 printf("%u,%u\n", v[0], v[1]);
 return 0;
}
>>>>

3. XXTEA Reverse Analysis

File Source: 2019 RCTF babyre
The task is to input a 16-character string, undergo multiple transformations, and finally output Bingo! Due to the nature of the problem, multiple solutions may exist, hence it must also satisfy md5(rctf{flag})==5f8243a662cf71bf31d2b2602638dc1d.
No further explanations will be provided here, as the main focus is on the reverse analysis of XXTEA. We will look at the most critical encryption function sub_55A0DF892CE0.
signed __int64 __fastcall sub_55A0DF892CE0(int *a1, signed int a2, __int64 a3)
{
 v3 = a3;
 v4 = a2;
 v5 = *a1;
 v43 = a2;
 if ( a2 > 1 )
 {
 v6 = a2 - 1;
 v7 = &a1[a2 - 1];
 v8 = 0;
 v9 = *v7;
 v10 = ((a2 - 4) & 0xFFFFFFFE) + 2;
 v45 = 0x9E3779B9 * (52 / a2) - 0x4AB325AA;
 do
 {
 v8 -= 0x61C88647;
 v11 = v8 >> 2;
 if ( v43 <= 3 )
 {
 v14 = 0;
 }
 else
 {
 v12 = *a1;
 v13 = a1;
 v14 = 0;
 do
 {
 v15 = v13[1];
 v13 += 2;
 v16 = (v9 ^ *(_DWORD *)(v3 + 4LL * (((unsigned __int8)v14 ^ (unsigned __int8)v11) & 3))) + (v15 ^ v8);
 v17 = v14 + 1;
 v14 += 2;
 v18 = v12 + ((((v9 >> 5) ^ 4 * v15) + ((v15 >> 3) ^ 16 * v9)) ^ v16);
 v12 = *v13;
 *(v13 - 2) = v18;
 v9 = v15 + (((4 * v12 ^ (v18 >> 5)) + (16 * v18 ^ (v12 >> 3))) ^ ((v12 ^ v8) + (v18 ^ *(_DWORD *)(v3 + 4LL * (((unsigned __int8)v11 ^ v17) & 3)))));
 *(v13 - 1) = v9;
 }
 while ( v10 != v14 );
 }
 v19 = &a1[v14];
 do
 {
 v20 = v19[1];
 v21 = v11 ^ v14++;
 ++v19;
 v22 = *(v19 - 1) + (((v9 ^ *(_DWORD *)(v3 + 4LL * (v21 & 3))) + (v20 ^ v8)) ^ ((16 * v9 ^ (v20 >> 3)) + ((v9 >> 5) ^ 4 * v20)));
 *(v19 - 1) = v22;
 v9 = v22;
 }
 while ( v6 > v14 );
 v9 = *v7 + (((v22 ^ *(_DWORD *)(v3 + 4LL * (((unsigned __int8)v6 ^ (unsigned __int8)v11) & 3))) + (*a1 ^ v8)) ^ ((4 * *a1 ^ (v22 >> 5)) + (16 * v22 ^ ((unsigned int)*a1 >> 3))));
 *v7 = v9;
 }
 while ( v8 != v45 );
 return 0LL;
 }
 result = 1LL;
 if ( a2 < -1 )
 {
 v24 = -a2;
 v25 = 0x9E3779B9 * (52 / v24 + 6);
 if ( v25 )
 {
 v26 = &a1[v24 - 1];
 v27 = ~v4;
 v44 = &a1[~v4];
 v28 = ~v4 - 2 - ((~v4 - 3) & 0xFFFFFFFE);
 do
 {
 v29 = v25 >> 2;
 if ( v27 <= 2 )
 {
 v31 = v27;
 }
 else
 {
 v30 = v44;
 v31 = v27;
 v32 = *v44;
 do
 {
 v33 = *(v30 - 1);
 v30 -= 2;
 v34 = v32;
 v32 = *v30;
 v35 = ((v5 ^ v25) + (v33 ^ *(_DWORD *)(v3 + 4LL * (((unsigned __int8)v31 ^ (unsigned __int8)v29) & 3)))) ^ ((4 * v5 ^ (v33 >> 5)) + ((v5 >> 3) ^ 16 * v33));
 v36 = v31 - 1;
 v31 -= 2;
 v37 = v34 - v35;
 v38 = *v30;
 v30[2] = v37;
 v5 = v33 - (((16 * v38 ^ (v37 >> 3)) + ((v32 >> 5) ^ 4 * v37)) ^ ((v32 ^ *(_DWORD *)(v3 + 4LL * (((unsigned __int8)v29 ^ v36) & 3))) + (v25 ^ v37)));
 v30[1] = v5;
 }
 while ( v28 != v31 );
 }
 v39 = &a1[v31];
 do
 {
 v40 = *(v39 - 1);
 --v39;
 v5 = v39[1] - (((v5 ^ v25) + (v40 ^ *(_DWORD *)(v3 + 4LL * (((unsigned __int8)v29 ^ (unsigned __int8)v31) & 3)))) ^ (((v5 >> 3) ^ 16 * v40) + ((v40 >> 5) ^ 4 * v5)));
 v39[1] = v5;
 --v31;
 }
 while ( v31 );
 v41 = *a1 - (((((unsigned int)*v26 >> 5) ^ 4 * v5) + (16 * *v26 ^ (v5 >> 3))) ^ ((*(_DWORD *)(v3 + 4LL * (v29 &amp; 3)) ^ *v26) + (v25 ^ v5)));
 v42 = v25 == 0x9E3779B9;
 v25 += 0x61C88647;
 v5 = v41;
 *a1 = v41;
 }
 while ( !v42 );
 }
 return 0LL;
 }
 return result;
}
We can see that the decompiled pseudo-code is also very clear. Throughout the entire function, the process revolves around the magic number 0x9E3779B9. Many may find this familiar; indeed! This function is structurally similar to the XXTEA encryption and decryption implementation discussed above.
sub_55A0DF892CE0(v, -(v10 >> 2), key); // stea(v,-2,key)
Combining other relevant information, it can be easily seen that the function parameters v are two 32-bit unsigned numbers, -(v10 >> 2) evaluates to -2, and key is a 128-bit key consisting of 0xE0C7E0C7, 0xC6F1D3D7, 0xC6D3C6D3, 0xC4D0D2CE. This calls the XXTEAdecode function to decrypt the two 32-bit unsigned numbers, and the decryption result is compared after being XORed with a constant.
The core algorithm of the entire task is XXTEA. As long as the algorithm is identified, reverse engineering becomes very simple. The logic is simply to input a hexadecimal string, then hexencode, resulting in a 64-bit unsigned number (i.e., two 32-bit unsigned numbers), and then use xxteadecrypt to get a new 64-bit unsigned number.
Here, the last byte’s value must be less than 0x4, and the value of the byte at position (8 – last byte’s value + 1) should be set to 00. After this, it undergoes some bitwise operations to verify whether the result equals 0x69e2. This step does not alter the original value and can be ignored. Finally, the verification checks if the byte XORed with 0x17 results in Bingo!
Combining the above, it is guessed that the value of the 7th byte is 00, the last byte’s value is 0x02, and md5(rctf{flag})==5f8243a662cf71bf31d2b2602638dc1d. This allows us to determine that the final decrypted value of the 64-bit unsigned number is 0x02XX367870797e55 (little-endian). A script can be written to brute-force the next highest 8 bits, which will yield the flag for this problem:
#include <openssl/md5.h>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <string>
using namespace std;
// -lcrypto
string MD5(const string&amp; src) {
 MD5_CTX ctx;
 
 string md5_string;
 unsigned char md[16] = {0};
 char tmp[33] = {0};
 
 MD5_Init(&amp;ctx);
 MD5_Update(&amp;ctx, src.c_str(), src.size());
 MD5_Final(md, &amp;ctx);
 
 for (int i = 0; i < 16; ++i) {
 memset(tmp, 0x00, sizeof(tmp));
 sprintf(tmp, "%02X", md[i]);
 md5_string += tmp;
 }
 return md5_string;
}
 
string aaa(unsigned int* v) {
 string str;
 for (size_t i = 0; i < 2; i++) {
 for (size_t j = 0; j < 8; j += 2) {
 unsigned char cur = v[i] &amp; 0xff;
 str += ((cur &amp; 0xf0) >> 4) < 10 ? (((cur &amp; 0xf0) >> 4) + 0x30)
 : (((cur &amp; 0xf0) >> 4) + 0x57);
 str += (cur &amp; 0x0f) < 10 ? ((cur &amp; 0x0f) + 0x30) : ((cur &amp; 0x0f) + 0x57);
 v[i] >>= 8;
 }
 }
 return str;
}
 
#define MX \
 ((z >> 5 ^ y << 2) + (y >> 3 ^ z << 4) ^ (sum ^ y) + (k[p &amp; 3 ^ e] ^ z))
bool btea(unsigned int* v, int n, unsigned int* k) {
 unsigned int z = v[n - 1], y = v[0], sum = 0, e, DELTA = 0x9e3779b9;
 unsigned int p, q;
 if (n > 1) { /* Coding Part */
 q = 6 + 52 / n;
 while (q-- > 0) {
 sum += DELTA;
 e = (sum >> 2) &amp; 3;
 for (p = 0; p < n - 1; p++)
 y = v[p + 1], z = v[p] += MX;
 y = v[0];
 z = v[n - 1] += MX;
 }
 return 0;
 } else if (n < -1) { /* Decoding Part */
 n = -n;
 q = 6 + 52 / n;
 sum = q * DELTA;
 while (sum != 0) {
 e = (sum >> 2) &amp; 3;
 for (p = n - 1; p > 0; p--)
 z = v[p - 1], y = v[p] -= MX;
 z = v[n - 1];
 y = v[0] -= MX;
 sum -= DELTA;
 }
 return 0;
 }
 return 1;
}
 
int main() {
 // 55 7e 79 70 78 36 xx 02
 unsigned int t[2] = {0x70797e55, 0x02003678};
 unsigned int v[2] = {0, 0};
 unsigned int key[4] = {0xE0C7E0C7, 0xC6F1D3D7, 0xC6D3C6D3, 0xC4D0D2CE};
 string flagmd5 = "5F8243A662CF71BF31D2B2602638DC1D";
 
 for (unsigned long long i = 0x0; i <= 0xff; i += 0x1) {
 v[0] = t[0];
 v[1] = t[1] | (i << 16);
 string flag = "";
 flag += "rctf{";
 btea(v, 2, key);
 flag += aaa(v);
 flag += "}";
 cout << flag << endl;
 if (MD5(flag) == flagmd5) {
 cout << "success!" << endl;
 cout << flag << endl;
 return 0;
 }
 }
 return 0;
}
>>>>

4. TX TEA Modified Algorithm

TX modified the TEA algorithm to 16 rounds (the minimum requirement for TEA security) and is widely used.
For related content, see here: Tencent TEA encryption algorithm
The main change is to modify the encryption rounds to 16 and implement an improved CBC mode of encryption.
>>>>

Summary

To identify the TEA series algorithms, one only needs to refer to the constant 0x9e3779b9 and its related encryption structure, which can easily determine whether it is TEA, XTEA, or XXTEA. After that, simply locate the ciphertext and encryption key, along with the above encryption and decryption implementation code, to quickly decrypt. The TEA algorithm in reverse analysis is generally quite clear after IDA decompilation. As long as one has a certain understanding, it can be easily recognized, and then dynamic debugging can verify. As for the findcrypto3 plugin recognition, it is also based on constant recognition, so knowing this feature is sufficient.
>>>>

6. Attachments

  • Source code for TEA series algorithms

  • 2019 RCTF babyre

>>>>

7. References

  • Tiny Encryption Algorithm
  • XTEA
  • XXTEA
  • TEA, XTEA, XXTEA encryption and decryption algorithms
  • Encryption and Decryption, 4th Edition – TEA Algorithm

Implementation and Reverse Analysis of Tiny Encryption Algorithm

– End –

Implementation and Reverse Analysis of Tiny Encryption Algorithm

KX ID:丿feng

https://bbs.pediy.com/user-809191.htm

* This article is original by KX forum 丿feng, please indicate the source from KX community when reprinting

Recommended articles++++

Implementation and Reverse Analysis of Tiny Encryption Algorithm

* Build your own PE interpreter

* Simple analysis of HW action rdpscan backdoor

* Personal analysis of CVE-2018-0802

* Representation of basic data types in C++

* Linux Kernel Exploit: Learning Kernel Vulnerabilities (3) – Bypass-Smep

﹀

﹀

﹀

Advanced Security Circle, a must-read bookImplementation and Reverse Analysis of Tiny Encryption Algorithm

﹀

﹀

﹀

Implementation and Reverse Analysis of Tiny Encryption Algorithm

Implementation and Reverse Analysis of Tiny Encryption Algorithm
Click “Read the original text” to recharge together!

Related posts

  1. Configuration Tutorial for Liuli on Raspberry Pi
  2. Research on Data Compliance Business Encryption Algorithms (Part 1)
  3. Three Powerful Encryption Algorithms
  4. Comprehensive STM32 Microcontroller Self-Learning Guide
  5. Tor Adds New Layer of Encryption with Selfrando
  6. What Are Encryption Algorithms?
  7. Malware Unpacking Methods (Part 2): Weak Encryption Algorithms
  8. The Evolution of Encryption Algorithms
  9. Analysis and Summary of Common Ransomware Encryption Algorithms
  10. Tor’s New Encryption Algorithm Enhances Anonymity
  11. Exploring Poco Util Net SSL Cipher Factory Manager in C++
  12. Exploring the Lightest Micro Robots: A Review of Innovations
  13. Comprehensive Learning Experience of STM32 Circuit Knowledge
  14. Hands-On Tutorial for STM32 Embedded Machine Learning (TinyML) – Part 1
  15. Implementing File System Interfaces in C#
  16. Kubernetes Learning Path for 2025
  17. Toshiba Launches Arm Cortex-M4 Microcontroller for Motor Control
  18. PRGdb: Plant R Gene Database Overview
  19. Human Anatomy: Adrenal Glands

Leave a Comment