
Analysis of Multimodal Multi-Objective Optimization
Multimodal multi-objective optimization via multi-operator adaptation and clustering-based environmental selection

1

Research Background
The characteristics of Multimodal Multi-Objective Optimization Problems (MMOPs) are the existence of multiple global or local Pareto optimal solution sets (PS) in the decision space. Although many evolutionary algorithms (MMOEAs) have been designed to address these problems, most algorithms rely on fixed operators to generate offspring, which can lead to an imbalance between convergence and diversity when facing complex and diverse optimization problems. To address this limitation, this paper proposes a Multi-Operator Adaptation Strategy that dynamically adjusts the proportion of each operator based on its success rate and combines it with a clustering-based environmental selection strategy to more effectively explore the solution space and maintain population diversity, thereby improving the algorithm’s performance and robustness in handling complex multimodal multi-objective optimization problems. This method not only leverages the advantages of multiple operators but also enhances adaptability to different optimization stages through hierarchical clustering techniques.

2

Current Research Status
Current research on multimodal multi-objective optimization (MMOPs) mainly focuses on finding multiple Pareto optimal solution sets through evolutionary algorithms and maintaining population diversity to ensure a wide distribution of solutions. However, most existing algorithms rely on a fixed single operator, which can lead to an imbalance between convergence and diversity when facing complex and diverse problems, while lacking adaptability to different optimization stages. To address these issues, some recent studies have proposed various improvement strategies, including adaptive operator adjustment and clustering-based selection methods, but these methods still face challenges of high computational complexity and insufficient diversity maintenance. The proposed MMOAOC algorithm dynamically adjusts the proportion of multiple operators and combines it with a clustering-based environmental selection mechanism to more effectively explore the solution space, improve algorithm performance and robustness, thereby overcoming the limitations of existing methods.

3

Research Method
This paper proposes a new algorithm, MMOAOC, which aims to more effectively explore the solution space and improve algorithm performance and robustness by dynamically adjusting operator proportions and combining it with a clustering-based environmental selection mechanism, thereby overcoming the limitations of existing methods.
3.1 Adaptive Multi-Operator Strategy
The Adaptive Multi-Operator Strategy is a core method proposed in this paper, aimed at improving the performance of multimodal multi-objective optimization algorithms by dynamically adjusting the proportions of different operators. The key to this strategy is to flexibly adjust the usage frequency of each operator based on its performance during the evolutionary process, thereby better balancing exploration and exploitation and enhancing the algorithm’s adaptability to different types of problems. Traditional evolutionary algorithms typically use only one operator (e.g., Genetic Algorithm GA or Differential Evolution DE). However, different operators have their own advantages when dealing with complex optimization problems. For example, GA excels at global search, while DE performs well in local search. The proposed Adaptive Multi-Operator Strategy simultaneously uses both GA and DE operators and dynamically adjusts their proportions based on their performance. The success rate (Success Rate, SR) of each operator is used to measure its ability to generate high-quality offspring. Specifically, successful individuals are those that can enter the next generation population.Based on the success rate, the proportion of each operator generating offspring is dynamically adjusted. If an operator has a high success rate, the number of offspring it generates is increased; conversely, it is decreased.The specific adjustment method is shown in Algorithm 1.

3.2 Clustering-Based Selection Mechanism
The clustering-based selection mechanism is an environmental selection strategy aimed at maintaining diversity in the population in both decision space and objective space. This mechanism first clusters the population in the decision space into several clusters and records the number of individuals in each cluster. It then prioritizes selecting those clusters that contain only a single individual, directly adding them to a temporary set to ensure that unique solutions are not lost. Next, the remaining clusters are sorted in ascending order based on the number of individuals, and for each individual in the cluster, its crowding distance relative to the individuals already in the temporary set in the objective space is calculated, selecting the individual with the maximum crowding distance to add to the temporary set, ensuring that the selected individuals are not only diverse but also represent different regions. Finally, the most representative and diverse individuals are selected to form the next generation population, effectively enhancing the algorithm’s exploration capability and global search performance in complex multimodal multi-objective optimization problems, ensuring a wide distribution of solutions and high-quality optimization results. This strategy combines clustering techniques and crowding distance calculations to dynamically balance convergence and diversity, thereby enhancing the overall robustness and adaptability of the algorithm. The specific algorithm is shown in Algorithm 2.

Figure 1 further illustrates this method: the initial population is divided into multiple clusters. For example, in the figure, the initial population is divided into four clusters, represented by different colors (blue, orange, yellow, and green). If a cluster contains only a single individual (e.g., p1 in the blue cluster), it is directly added to the temporary set R. This is because these unique solutions should not be lost. For clusters containing multiple individuals, they are sorted in ascending order based on the number of individuals. Then, within each cluster, the individual with the maximum crowding distance relative to the individuals in set R is selected to join R. This step aims to maintain diversity in the objective space. For the orange, yellow, and green clusters, the same process is repeated until all clusters have been processed. Ultimately, set R contains the most representative and diverse individuals selected from each cluster. These individuals are part of the next generation population, ensuring diversity in both decision space and objective space.
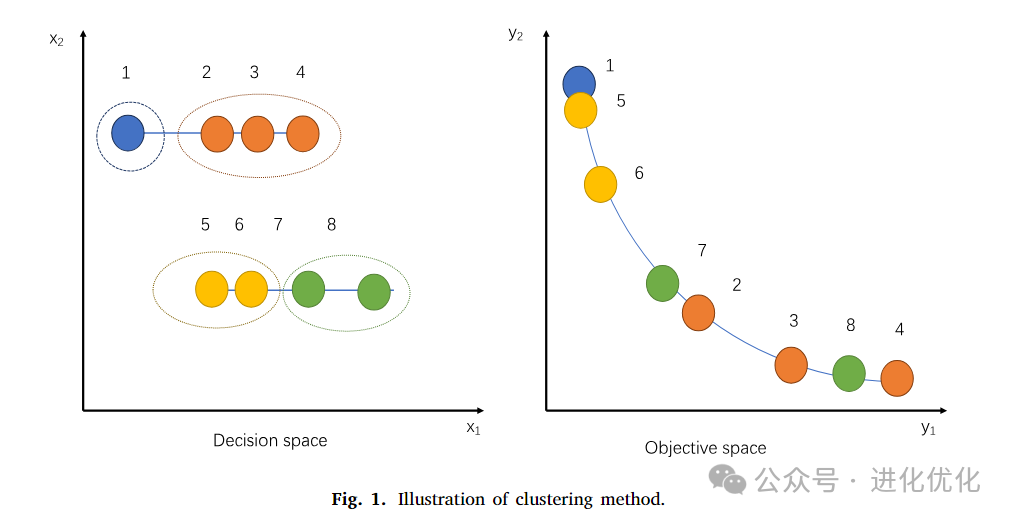
3.3 Environmental Selection
This environmental selection method first merges the initial population and offspring, performs non-dominated sorting on the merged population, obtaining the front number (FNo) and maximum front number (MaxFNo) for each individual, and adopts corresponding strategies based on different situations: when exactly N individuals satisfy FNo less than or equal to MaxFNo, these individuals are directly selected for the next generation; when there are multiple front layers (MaxFNo > 1), individuals from lower front layers are prioritized, and crowding distance is used to further filter individuals from higher front layers; when all individuals are in the same front layer (MaxFNo = 1), a clustering-based selection mechanism is employed, grouping individuals through clustering and selecting the most representative individuals from each cluster based on crowding distance for the next generation. This method combines non-dominated sorting, crowding distance calculation, and clustering techniques to ensure that the algorithm maintains good diversity and uniform distribution in both decision space and objective space, thereby improving overall optimization performance and robustness. Ultimately, by dynamically adjusting the proportions of operators, the algorithm’s adaptability to different optimization stages is further enhanced. The specific algorithm is shown in Algorithm 3.

3.4 Overall Framework of MMOAOC
The overall framework of MMOAOC includes four main steps: first, randomly initializing the population and setting the initial operator proportions; then, in each iteration, generating offspring using Genetic Algorithm (GA) and Differential Evolution (DE) based on the current proportions, and selecting parent individuals through tournament selection; next, applying an environmental selection mechanism based on non-dominated sorting, crowding distance calculation, and clustering techniques to select the most representative and diverse individuals from the merged population and offspring to form the next generation population; finally, dynamically adjusting the proportions of each operator based on their success rates to balance exploration and exploitation capabilities, ensuring the algorithm’s adaptability and robustness in different optimization stages. This comprehensive strategy effectively improves the algorithm’s performance in complex multimodal multi-objective optimization problems. The overall algorithm framework is shown in Algorithm 4.


4

Experimental Results
This study conducted five experiments to verify the effectiveness of the proposed method, including comparative experiments on the MMF test suite, comparative experiments on the MMMOP test suite, effectiveness analysis experiments of the proposed strategy, parameter sensitivity analysis experiments, and comparative experiments on real MMOPs with representative algorithms.
4.1 Comparative Experiments on the MMF Test Suite
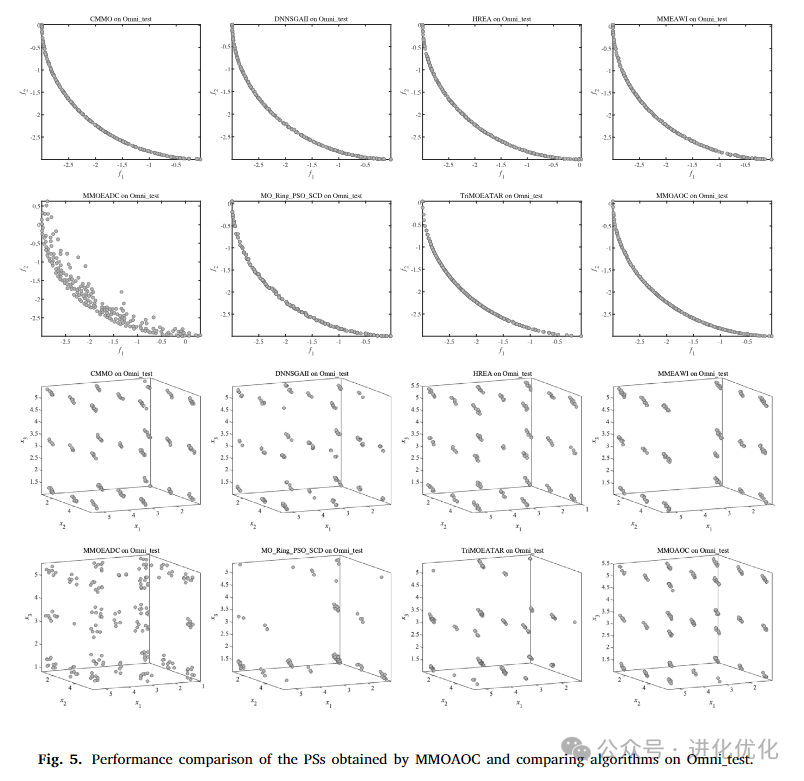
The purpose of this experiment is to evaluate the performance of the MMOAOC algorithm on the MMF benchmark suite, which is one of the fundamental benchmarks for evaluating MMOEAs. The MMF series test problems are characterized by their variety of PS and PF shapes, allowing for a comprehensive assessment of algorithm performance.Figures 2 to 5 compare the PFs and PS sets obtained by the comparative algorithms and the MMOAOC algorithm on the MMF2, MMF4, MMF8, and OMNI test problems. These figures indicate that the proposed MMOAOC significantly outperforms other comparative algorithms in terms of PF quality in the objective space. Additionally, MMOAOC generates well-distributed solution sets and successfully identifies all PSs for each problem. In summary, compared to the comparative MMOP algorithms, MMOAOC provides a superior solution set.
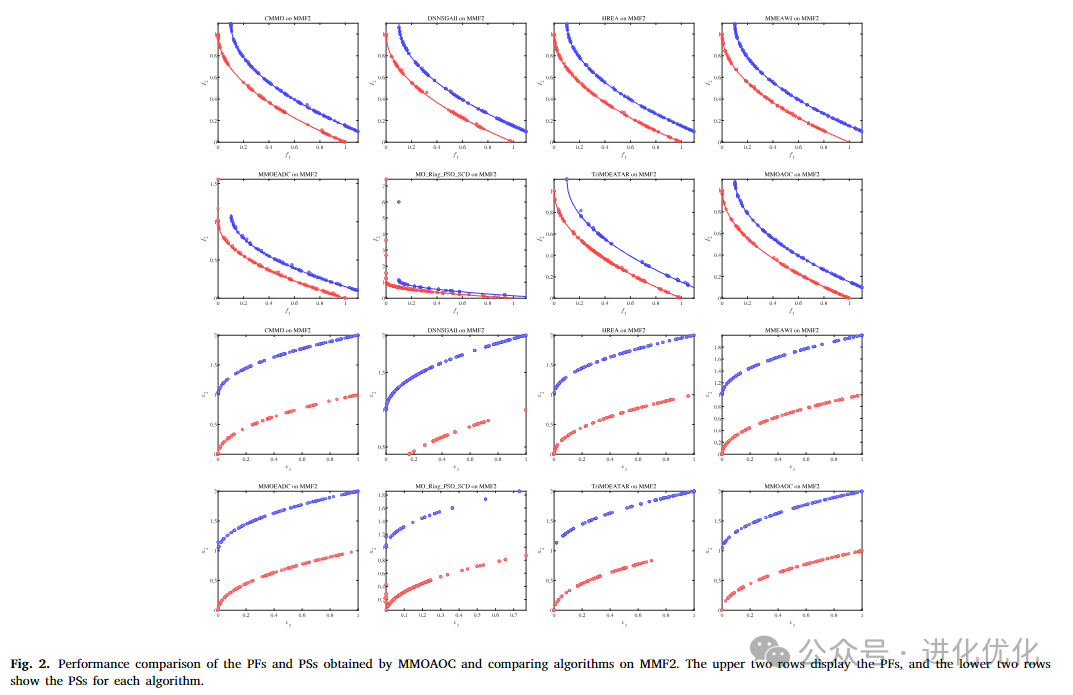
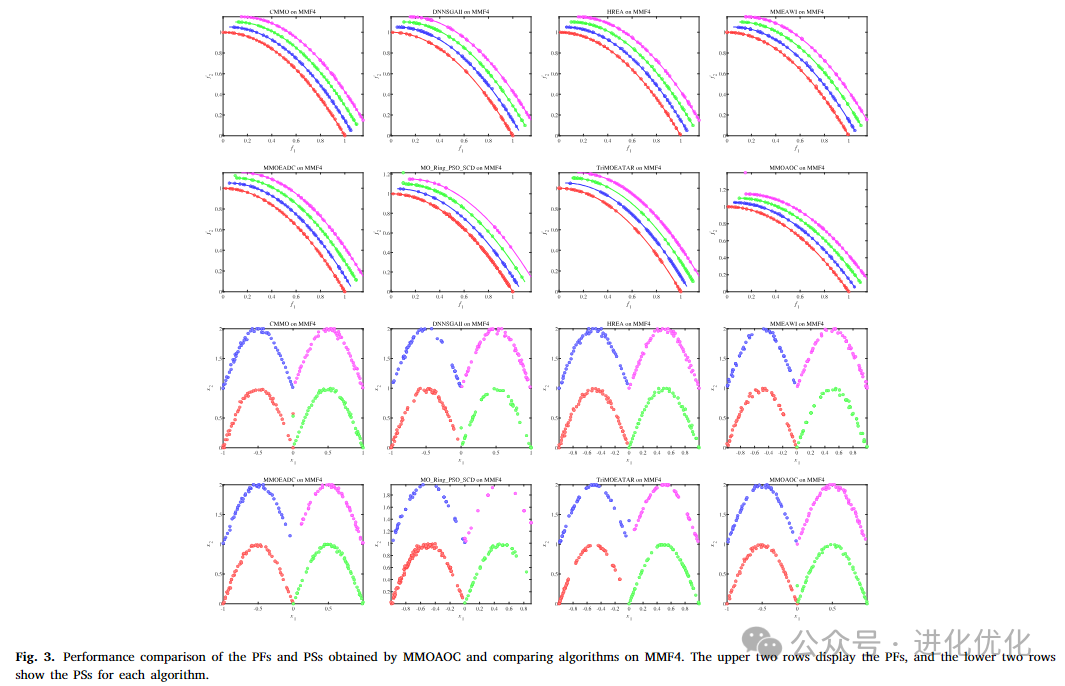
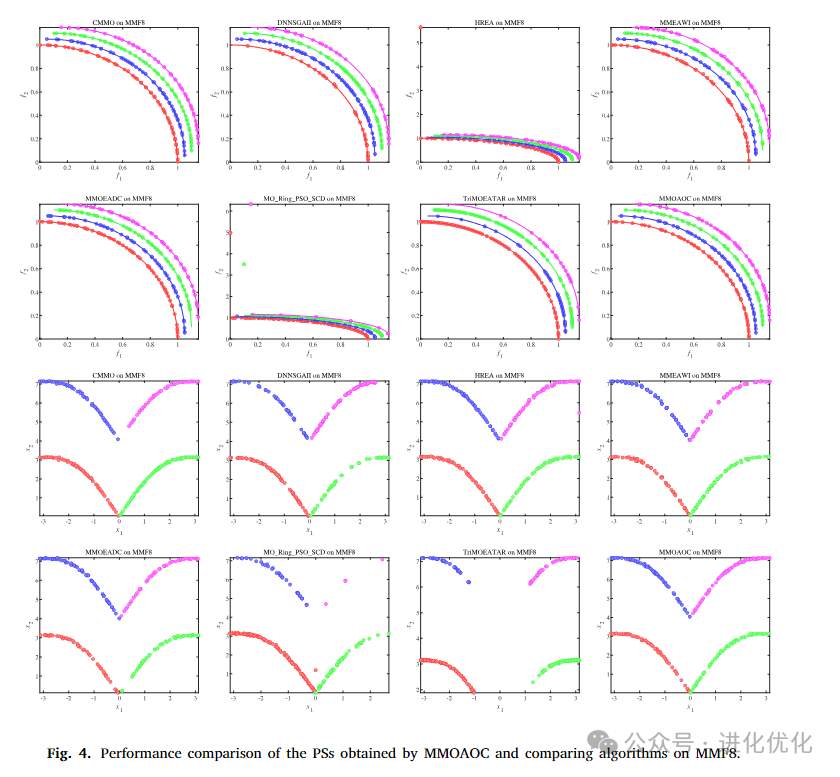
4.2 Comparative Experiments on the MMMOP Test Suite
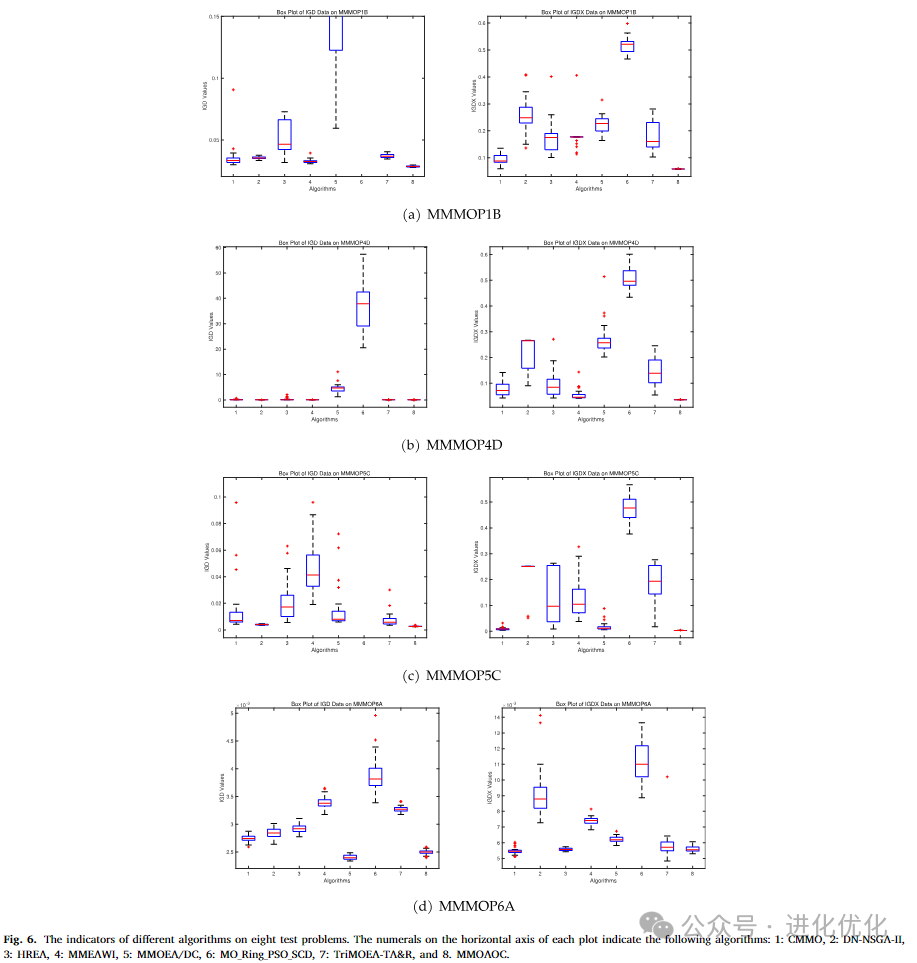
MMMOP test suite is highly scalable, including 20 problems with varying numbers of PSs and higher-dimensional objectives and decision spaces with mixed interactions. The complex nature of MMMOP poses challenges for MMOEA in maintaining diversity and robustness of the solution set. Figure 6 presents box plot analyses of four MMMOPs from 31 independent runs. Two metrics, IGD and IGDX, are used to evaluate the representative function values. On the horizontal axis, CMMO, DN-NSGA-IIHREA, MMEAWI, MMOEA/DC, MO_RING_PSO_SCD, TRIMOEA-TA&R, and MMOAOC are numbered from 1 to 8. The red line indicates the median metric value for each problem. From these figures, it is evident that our algorithm has a relatively low median value compared to competitive algorithms, indicating that it finds solutions closer to the true Pareto front in most cases. The blue rectangles represent the interquartile range of the middle 50% of the data, i.e., the distance from the first quartile to the third quartile. From the figures, it can be seen that the box for MMOAOC is narrower, indicating that its performance is more stable across multiple runs, with less fluctuation in results. Therefore, MMOAOC overall performs best across various test problems, with the lowest median, narrowest box, and fewest outliers, demonstrating its superiority and stability under various testing conditions.
4.3 Effectiveness Analysis of the Strategy
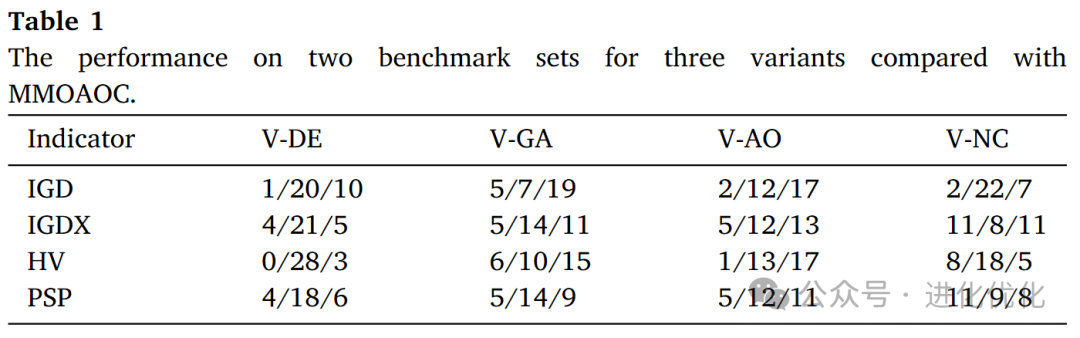
This section studies the impact of dynamically combining multiple operators to generate individuals on the algorithm’s results. Table 1 presents a performance comparison of four variant algorithms (V-DE, V-GA, V-AO, and V-NC) with MMOAOC on two benchmark test sets, measured by four standard evaluation metrics (IGD, IGDX, HV, and PSP). Specifically, V-DE uses only the Differential Evolution (DE) operator, V-GA uses only the Genetic Algorithm (GA) operator, while V-AO adopts a fixed proportion of operators (50% DE and 50% GA) without dynamic adjustment. V-NC uses the crowding distance calculation method from SPEA2, calculating crowding distances between individuals in decision space and objective space, and assigning a comprehensive crowding distance value to each individual. This value is obtained by a weighted average of crowding distances in both spaces, typically with a weight of 0.5 each.
The values of each metric represent the relative performance of different algorithms over 31 independent runs, recording the best, second-best, and worst cases for each algorithm on the test problems. Overall, the data in Table 1 indicates that although V-DE, V-GA, and V-AO each perform well in certain specific cases, their performance is inferior to MMOAOC in most test problems. V-NC performs well on certain metrics, particularly the IGDX metric in decision space, but its overall performance and stability still do not match MMOAOC. In summary, MMOAOC achieves better overall performance across multiple metrics through its adaptive multi-operator strategy and clustering-based selection mechanism, demonstrating higher robustness and consistency. This highlights the importance of dynamically adjusting operator proportions and combining various selection mechanisms, effectively improving the algorithm’s performance in complex multimodal multi-objective optimization problems.
4.4 Parameter Sensitivity Analysis Experiment
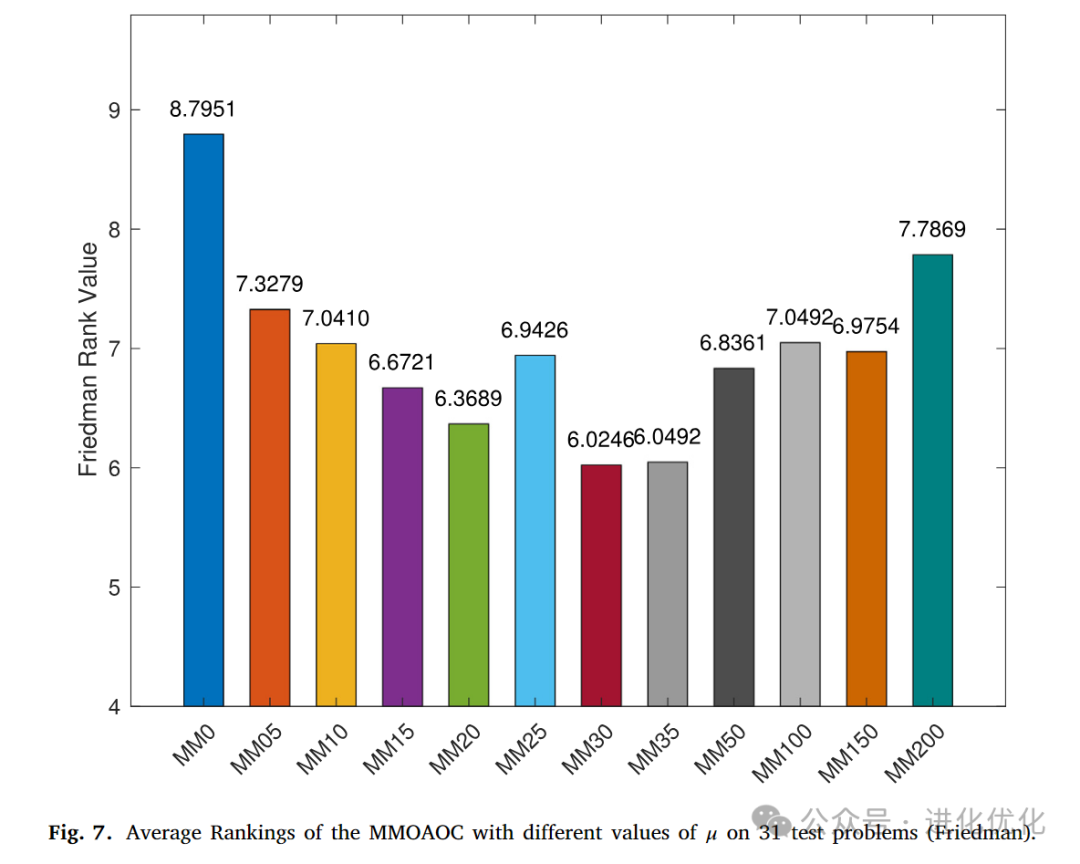
This paper introduces a predefined parameter 𝜇, which controls the rate of adjustment of the operator ratios in the MMOAOC algorithm. The choice of 𝜇 is crucial for balancing the algorithm’s adaptability and stability. The reason is that a larger 𝜇 leads to rapid adjustments of the ratios, resulting in frequent changes in operator proportions. Although this can accelerate adaptation, it may also reduce the algorithm’s stability. Conversely, a very small value of 𝜇 leads to slow adjustments, which may hinder the algorithm’s ability to adapt effectively to the problem, resulting in unnecessary computations. To study the impact of different 𝜇 settings, we define the range of 𝜇 values for the algorithm from 0 to 0.2. For each variant, the 𝜇 value is set to 0.001 * 𝑛𝑢𝑚, where 𝑛𝑢𝑚 is the suffix of the variant’s name MM𝑛𝑢𝑚.
Figure 7 shows the average ranking of the MMOAOC algorithm under different 𝜇 value settings across 31 test problems, using the Friedman test method. Specifically, this figure evaluates the impact of changing the parameter 𝜇 on the performance of the MMOAOC algorithm. The results show that when 𝜇 is set to 0.003, the algorithm performs best, achieving the highest average ranking across all test problems. As the value of 𝜇 gradually increases from 0 to 0.003, the performance of the algorithm improves step by step, indicating that an appropriate value of 𝜇 can significantly enhance the algorithm’s adaptability and stability. However, when the value of 𝜇 exceeds 0.003, the performance of the algorithm begins to decline, as excessively high values of 𝜇 lead to frequent changes in operator proportions, affecting the algorithm’s stability and exploration capability. Therefore, Figure 7 emphasizes the importance of selecting an appropriate value of 𝜇 to balance the algorithm’s exploration and exploitation capabilities, confirming that 𝜇=0.003 is the optimal choice for optimizing the MMOAOC algorithm.
4.5 Comparative Experiments on Real MMOPs and Representative Algorithms
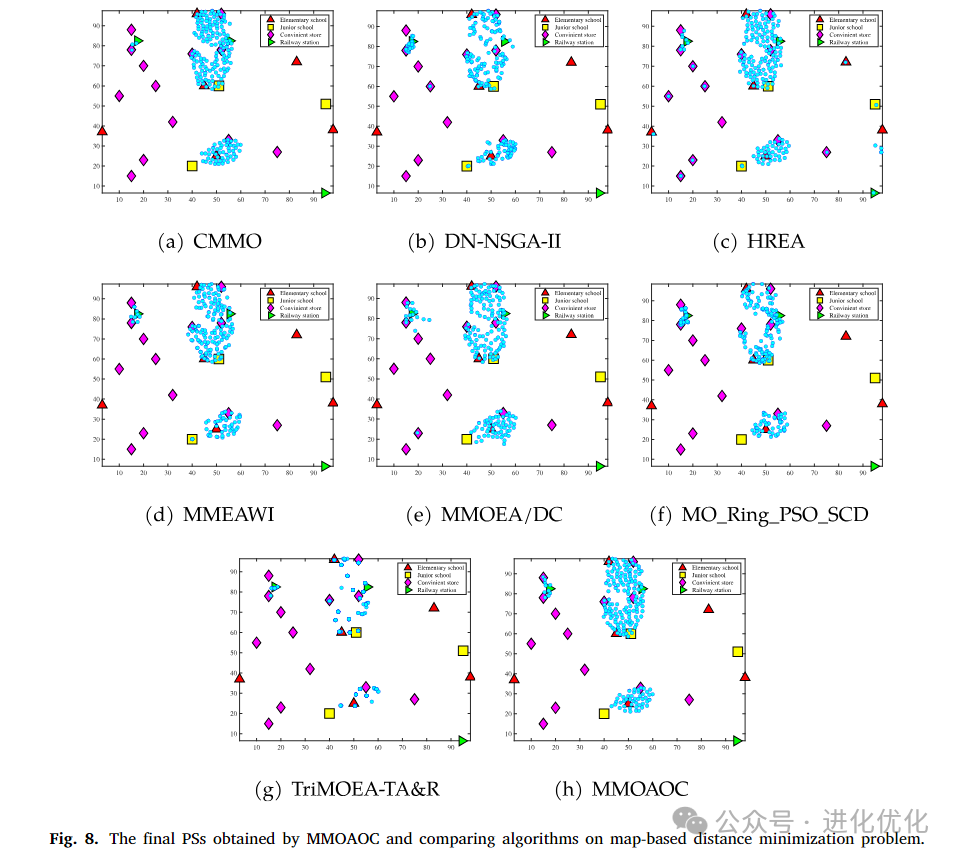
The test problem for this experiment is a simplified distance minimization problem. Table 2 presents the IGD values of different algorithms on multimodal multi-objective problems, used to evaluate the distance between the Pareto front found by each algorithm and the true Pareto front. Specifically, the table lists the IGD values of eight algorithms on specific test problems and their relative performance. Lower IGD values indicate that the solutions found by the algorithm are closer to the true Pareto front. The results show that the MMOAOC algorithm achieves the lowest or near-lowest IGD values on most test problems, indicating its high performance and robustness in multimodal multi-objective optimization problems, effectively finding high-quality and evenly distributed solutions. This demonstrates the advantages of MMOAOC in handling complex multi-objective optimization problems. Table 3 provides a detailed comparison of the performance of eight algorithms on multimodal multi-objective location problems using the IGDX metric. The results show that the MMOAOC algorithm achieves lower IGDX values on most test problems, indicating that the solutions found in decision space are closer to the true Pareto front and more evenly distributed. Figure 8 visually demonstrates the performance of MMOAOC and other comparative algorithms on this problem. The results show that MMOAOC not only finds high-quality solutions across multiple objectives but also maintains diversity and uniform distribution of solutions, thereby exhibiting significant advantages in complex multimodal multi-objective optimization problems. This result further validates the effectiveness of the adaptive operator strategy and clustering-based selection mechanism of MMOAOC, proving its superior performance in practical applications.
Table 4 provides a detailed comparison of the performance of seven algorithms on multi-objective neural architecture search problems using the HV metric. The results show that the MMOAOC algorithm achieves higher HV values in most cases, indicating that the Pareto front it finds is not only of high quality but also has a wide coverage. Although in some problems, the performance of MMOAOC is comparable to CMMO, overall, MMOAOC demonstrates superior performance and robustness across multiple problems, confirming the effectiveness of its adaptive operator strategy and clustering-based selection mechanism. This result further validates the advantages of MMOAOC in complex multimodal multi-objective optimization problems and highlights its potential in practical applications.




5

Conclusion and Outlook
5.1 Conclusion
This paper proposes an innovative multimodal multi-objective optimization algorithm (MMOAOC), which effectively addresses the challenges of balancing diversity and convergence in complex optimization problems through an adaptive multi-operator strategy and a clustering-based selection mechanism. Experimental results show that MMOAOC significantly outperforms existing algorithms in performance metrics such as IGD, IGDX, and HV across multiple benchmark test sets and practical application problems, demonstrating its exceptional optimization capability and robustness. Particularly in multimodal multi-objective distance minimization problems and neural architecture search problems, MMOAOC not only finds solutions closer to the true Pareto front but also maintains a uniform distribution of these solutions in both decision space and objective space.
5.2 Outlook
Future research can further explore the application potential and technical improvement directions of the MMOAOC algorithm. On one hand, it can be extended to larger-scale and more complex practical problems, such as large-scale neural network architecture search or multi-objective path planning, to verify its applicability and efficiency in different fields; on the other hand, by introducing more types of operators (such as Particle Swarm Optimization PSO, Ant Colony Optimization ACO) and intelligent parameter tuning methods (such as Bayesian optimization, reinforcement learning), the algorithm’s exploration and exploitation capabilities can be further enhanced. Additionally, research can investigate how to combine MMOAOC with other advanced technologies (such as machine learning, deep learning) to develop a more intelligent and efficient optimization framework to tackle increasingly complex real-world challenges. These studies will further advance the progress and development of the multimodal multi-objective optimization field.



Authors: Wu X, Ming F, Gong W, et al. Multimodal multi-objective optimization via multi-operator adaptation and clustering-based environmental selection [J]. Swarm and Evolutionary Computation, 2025, 96: 101962–101962.



Editor: Wei Xinping
Illustration: Wei Xinping
Click the blue text to follow us