
Analysis of the Paper
Multi-Strategy Multi-Objective Differential Evolutionary Algorithm with Reinforcement Learning

1

Research Background
Multi-objective optimization problems (MOPs) are very common and important in practical applications. Due to the inherent conflicts between different objectives, MOPs usually do not have a single optimal solution but rather a set of optimal solutions known as the Pareto optimal solution set. To find these solutions, multi-objective evolutionary algorithms (MOEAs) have been widely studied and applied, demonstrating their ability to solve complex MOPs. However, despite significant progress in MOEAs, effectively balancing exploration and exploitation during the search process remains a challenge, especially when dealing with problems that have irregular Pareto fronts, where traditional fixed-reference-point-based MOEAs perform poorly. To address these issues, this paper proposes a Reinforcement Learning-based Multi-Strategy Multi-Objective Differential Evolution Algorithm (RLMMDE).

2

Current Research Status
In multi-objective optimization problems, current research presents a multidimensional characteristic. In terms of multi-strategy and multi-crossover evolution, numerous algorithms have been proposed for both single-objective and multi-objective evolutionary algorithms. Different mutation strategies and crossover operators are combined to balance the exploration and exploitation capabilities of the algorithm, enhancing its performance. In the field of reinforcement learning-based evolutionary algorithms, reinforcement learning has been widely applied to parameter adaptation and strategy selection in evolutionary algorithms, but its application in multi-objective algorithms is relatively scarce, and related research needs further expansion. For reference point adaptive methods, there is insufficient balance between exploration (finding new potential solution spaces) and exploitation (deepening known promising areas), and the fixed reference point set struggles to adapt to dynamically changing optimization needs. Therefore, this paper proposes RLMMDE, aiming to improve algorithm performance by adaptively selecting different mutation and crossover strategies. Additionally, the algorithm employs reinforcement learning techniques to dynamically adjust parameter settings to further enhance efficiency and effectiveness.

3

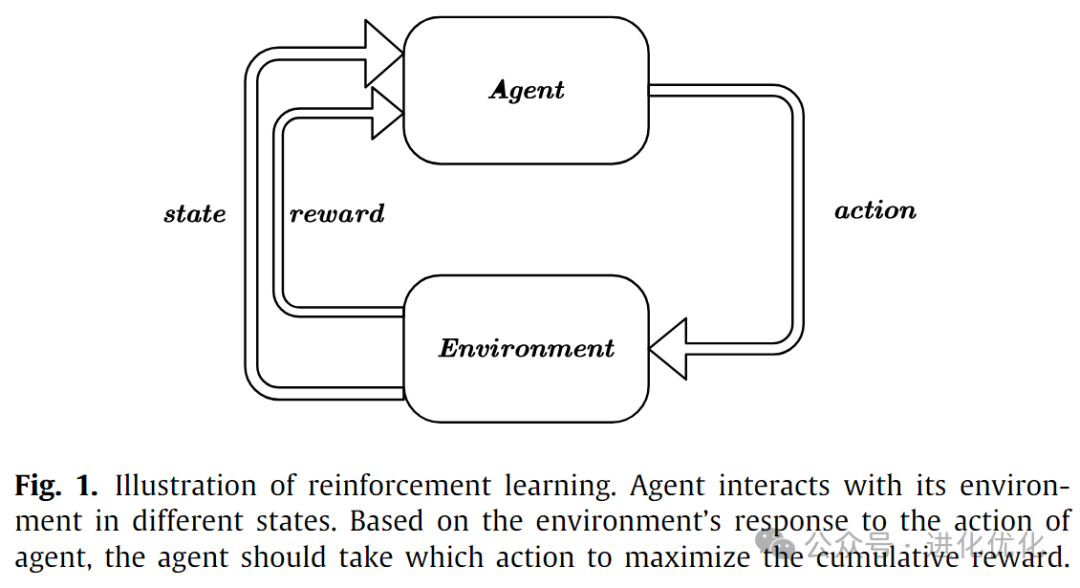
This article proposes a Reinforcement Learning-based Multi-Strategy Multi-Objective Differential Evolution Algorithm (RLMMDE), introducing an adaptive reference point activation mechanism and reference point adaptation method, aiming to better balance exploration and exploitation and ensure that the solution set is evenly distributed along the actual Pareto front. Reinforcement learning (RL) is a field of machine learning and a branch of artificial intelligence. As shown in Figure 1, reinforcement learning focuses on how artificial intelligence interacts with its environment in different states. Based on the environment’s response to previous interactions, the AI agent takes actions to maximize cumulative rewards. Due to this characteristic of reinforcement learning, it has been widely applied in evolutionary algorithms (EAs). In various RL-based EAs, it is mainly used for adaptive adjustment of control parameters and adaptive selection of strategies or operators.
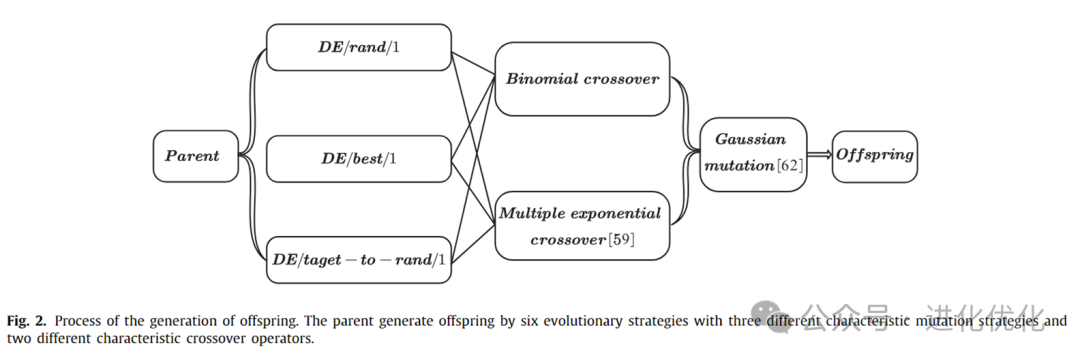
3.1 Multi-Strategy Multi-Crossover DE Optimizer
This paper uses a DE optimizer with multiple strategies and crossover operators. As shown in Figure 2, this optimizer employs six evolutionary strategies composed of three mutation strategies with different characteristics and two crossover operators to generate offspring. Additionally, the roulette wheel selection method is used to select the currently most suitable evolutionary strategy for each individual. However, these evolutionary strategies were initially designed for single-objective optimization problems and are not suitable for multi-objective optimization problems in certain aspects. Therefore, some significant modifications were made to the original method.In the multi-strategy and multi-crossover DE optimizer, three strategies with different characteristics are used: DE/rand/1, DE/best/1, and DE/target-to-rand/1. For the selection of crossover operators, classical binomial crossover with better problem universality and multi-exponential recombination with better handling of dependent variables are used.
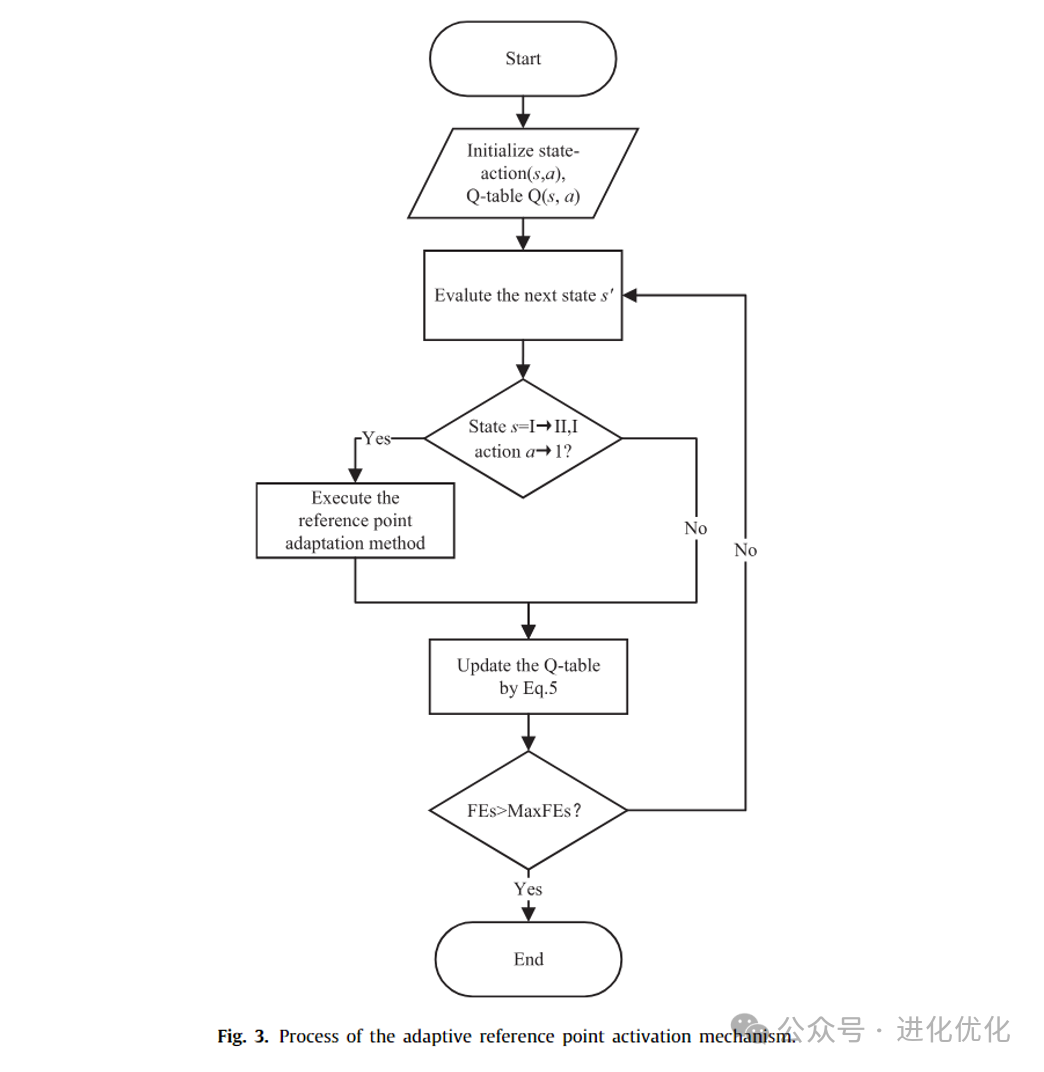
3.2 Reinforcement Learning-based Adaptive Reference Point Activation Mechanism
The reinforcement learning-based adaptive reference point activation mechanism dynamically decides whether to adjust reference points based on the current population state and reference point utilization rate using the Q-learning method in reinforcement learning, guiding the algorithm to explore the solution space more effectively during the multi-objective optimization process. This mechanism first initializes state-action pairs and their Q-table, and evaluates the number of unassociated individuals in each generation to determine whether reference point adjustment is necessary. If the number of unassociated individuals exceeds a set threshold, the reference point adjustment process is triggered, and the corresponding values in the Q-table are updated to reflect the quality of the action taken, optimizing guidance for future decisions. This method effectively overcomes the limitations of fixed reference points when dealing with complex or irregular Pareto front problems, enhancing the algorithm’s adaptability to diverse problems and the quality of solutions. The process of the adaptive reference point activation mechanism is shown in Figure 3, where states I and II are determined based on the association between reference points and individuals. For each individual and each reference point, the distance between them is calculated. The vertical distance from the individual’s objective function value to the ideal line (or hyperplane) defined by the reference points is computed. Based on the calculated distances, each individual is assigned to the nearest reference point. This means that each individual will be assigned to a specific reference point, indicating an association between them.
3.3 A Reference Point Adaptive Method
It is known that reference point-based MOEAs use a predetermined set of reference points to guide the entire evolutionary phase. Such a set plays an important role in ensuring that the obtained candidate solutions are as evenly distributed along the Pareto front as possible. Maintaining fixed reference points throughout the evolutionary process may lead to poor algorithm performance on certain MOPs. To improve the performance of the proposed algorithm, a reference point adaptive method is introduced. It is worth noting that overly frequent changes in reference points may negatively impact the algorithm’s convergence. To mitigate this issue, the reference point adaptive method is not employed during the initial stages of evolution. In this study, reference point adjustments only begin after 0.8 * MaxFE. The reference point adaptive method includes the following steps:Remove useless reference points: Remove reference points that have no associated individuals, simplifying the reference point set.Calculate the number of new reference points to be added: Based on the association between the current population and reference points, calculate the number of new reference points needed to be added. For example, if it is found that the number of individuals under certain reference points far exceeds that of others, several new reference points may need to be added to balance this unevenness.Select individuals farthest from the current reference points: Calculate the distance from each individual to the nearest reference point and select several individuals with the maximum distance as candidates for new reference points.Randomly select new reference points: Randomly select several individuals from the selected candidates as new reference points and add them to the reference point set.

4

Experiments in this Paper
This study conducted four experiments to verify the effectiveness of the proposed method, including comparisons of RLMMDE with traditional MOEAs, comparisons with MOEAs using different optimizers, comparisons with MOEAs using reference point adaptation, and performance comparisons with other test instances.
4.1 Comparison Experiment with Traditional MOEAs
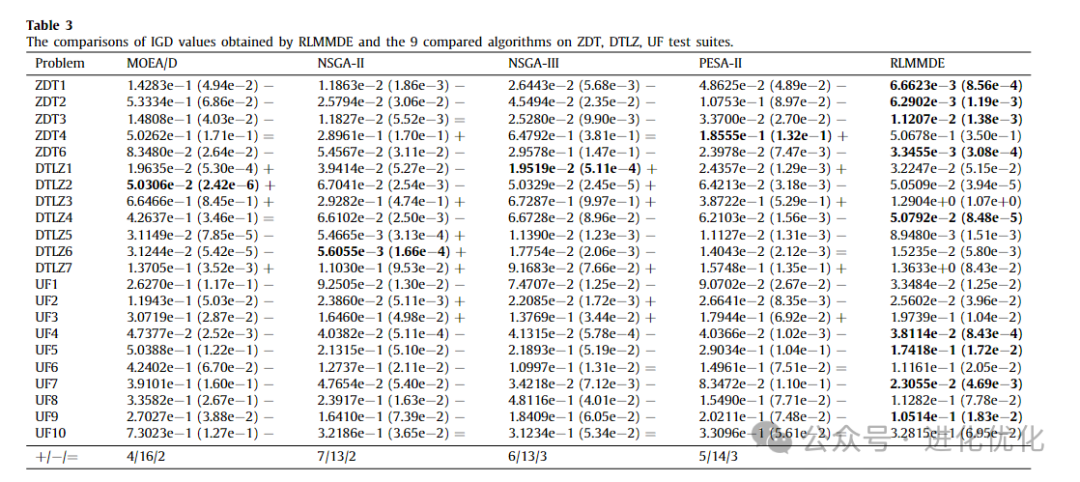
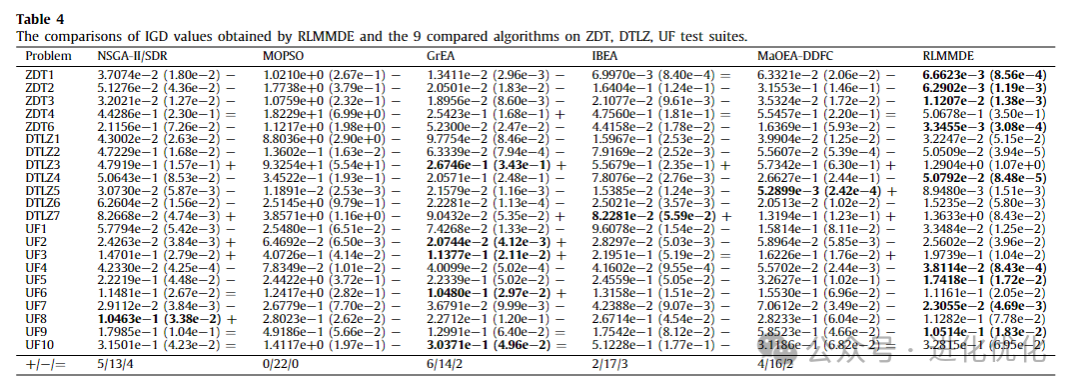
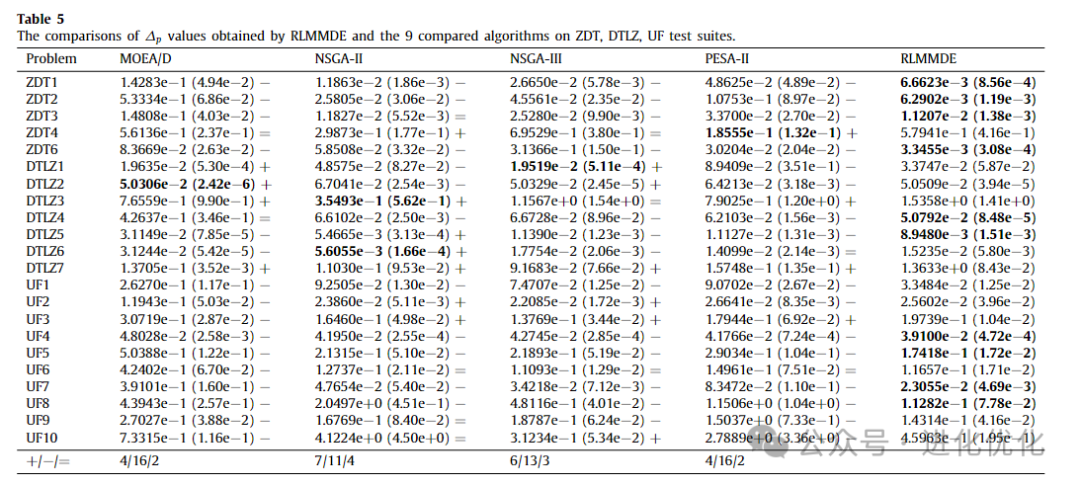
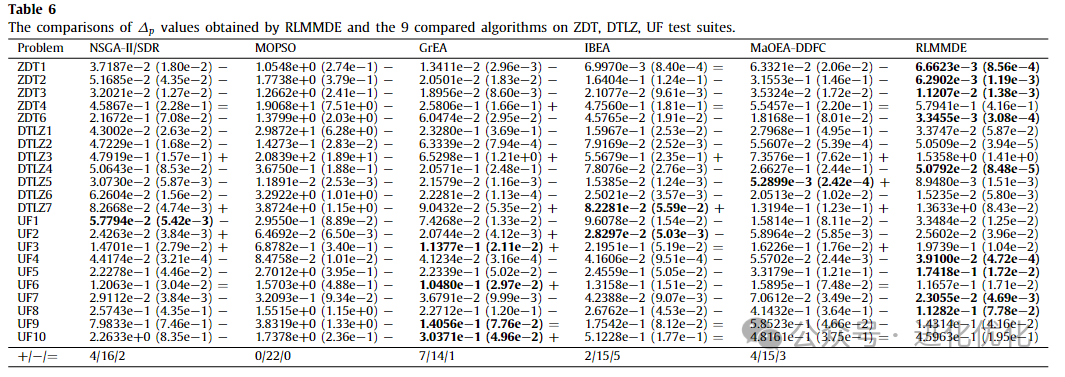
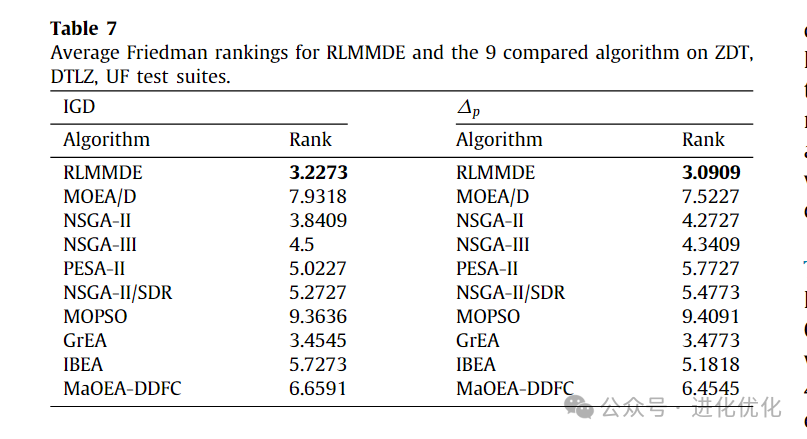
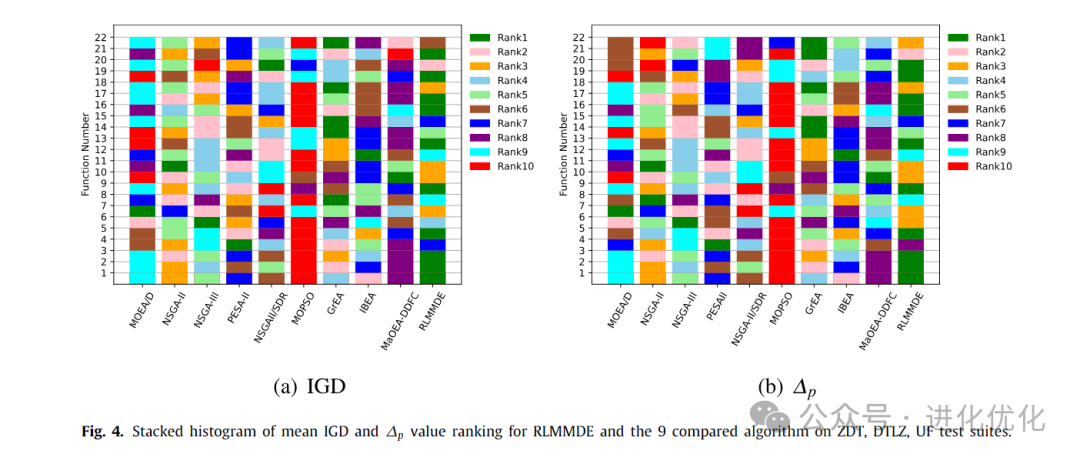
To verify the performance of the proposed algorithm, we compared RLMMDE with traditional MOEAs, with detailed test results shown in Tables 3-6. In these tables, the IGD and ∆p values obtained by solving these test suites using RLMMDE and traditional MOEAs are presented. As shown in Tables 3 and 4, in the experimental results of the IGD metric, the performance of RLMMDE significantly outperforms the other 9 comparison algorithms. On these 22 test problems from 3 different test suites, RLMMDE obtained 10 optimal solutions. Since RLMMDE used an environmental selection strategy in NSGA-III, it may be thought that this is the effect of that strategy. However, the results show that, under the same parameter settings, the proposed algorithm achieved better results than NSGA-III. Furthermore, RLMMDE obtained 9 better results compared to NSGA-III. This may be because the proposed multi-strategy and multi-crossover DE optimizer plays a good role in balancing the convergence and diversity of these problems. Additionally, the proposed reference point adaptive method further enhances RLMMDE’s performance in handling irregular Pareto front problems. Since NSGA-III uses a single operator and fixed reference points, this may be a reason affecting its performance. From Tables 5 and 6, it can be seen that in the experimental results of the ∆p metric, RLMMDE obtained 9 optimal solutions. From the last row of the table, it can be seen that RLMMDE has at least 11 better results than other comparison algorithms. It is noteworthy that the IGD and ∆p metrics obtained very similar results on certain test problems. This may be because the ∆p metric is composed of GD and IGD metrics, which have similar properties to the IGD metric. Furthermore, to further demonstrate the experimental results of RLMMDE and the 9 algorithms compared on the 22 test problems, Table 7 and Figure 4 show the average rankings after the Friedman test and the stacked histogram of average IGD and ∆p value rankings. From Table 7, it can be seen that RLMMDE achieved the best ranking in both IGD and ∆p values. From Figure 4, it can be seen that RLMMDE occupies the majority in the green blocks, indicating that it achieved the best results and has the best performance, followed by GrEA. Finally, in terms of average ranking, average IGD, and ∆p value rankings, the proposed RLMMDE is more competitive among the comparison algorithms.
4.2 Comparison Experiment with MOEAs Using Different Optimizers
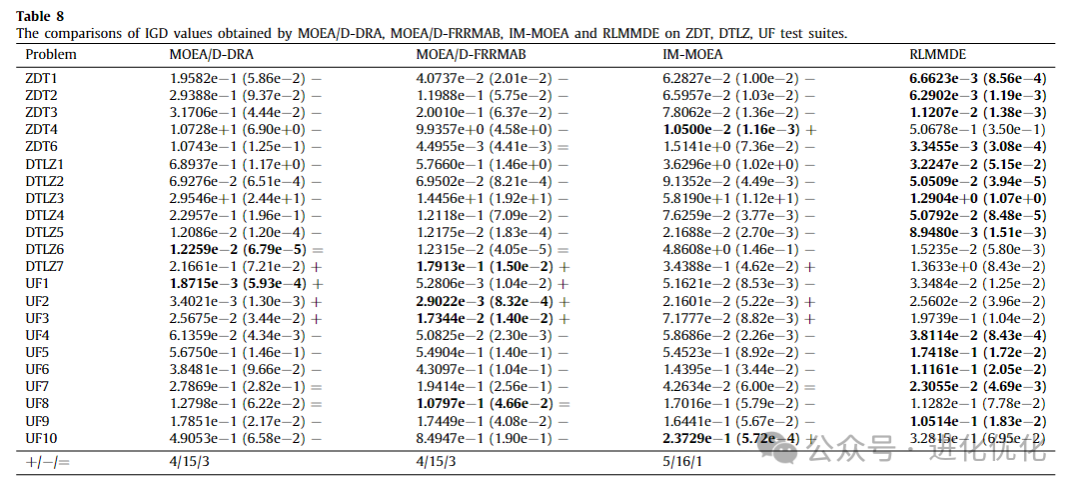
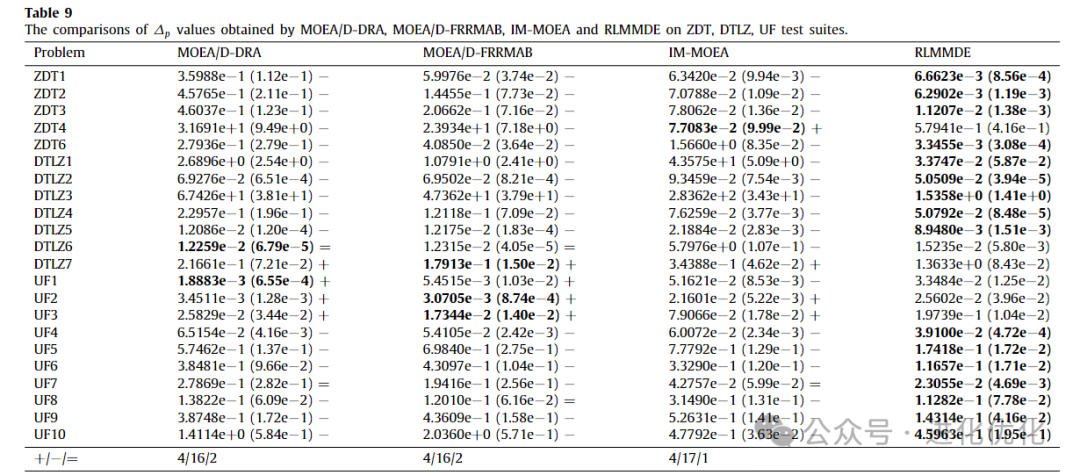
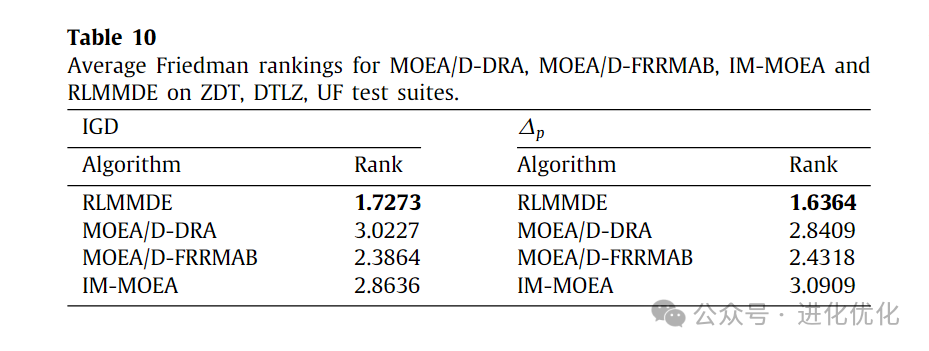
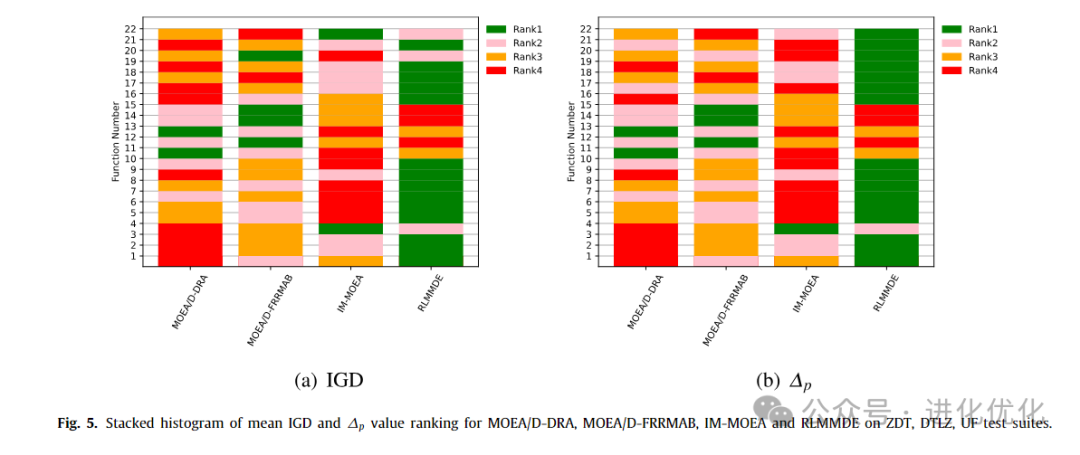
To compare the performance of RLMMDE with MOEAs using different types of optimizers, RLMMDE was compared with second-class algorithms (i.e., MOEA/DD-DRA, MOEA/D-FRMAB, and IM-MOEA), with detailed test results shown in Tables 8 and 9. In these two tables, the IGD and ∆P values obtained by RLMMDE and different types of optimizers are presented. The experimental results of the IGD metric are shown in Table 8, where RLMMDE significantly outperforms the other 3 comparison algorithms. On 22 test problems, RLMMDE obtained 14 optimal solutions. From Table 9, it can be seen that for the experimental results of the ∆p metric, RLMMDE obtained 16 optimal solutions on these 22 test problems. Additionally, to further analyze the experimental results of RLMMDE and the three comparison algorithms on the 22 test problems, the average rankings after the Friedman test are shown in Table 10, and the stacked histogram of average IGD and ∆p value rankings is shown in Figure 5. From Table 10, it can be seen that RLMMDE ranks first in both IGD and ∆p values, followed by MOEA/D-FRMAB. As shown in Figure 5, RLMMDE occupies the most green blocks, indicating that it achieved the best results and has the best performance. Finally, in terms of average ranking, average IGD, and ∆p value rankings, the proposed RLMMDE is more competitive among the comparison algorithms.
4.3 Comparison Experiment with MOEAs Using Reference Point Adaptation
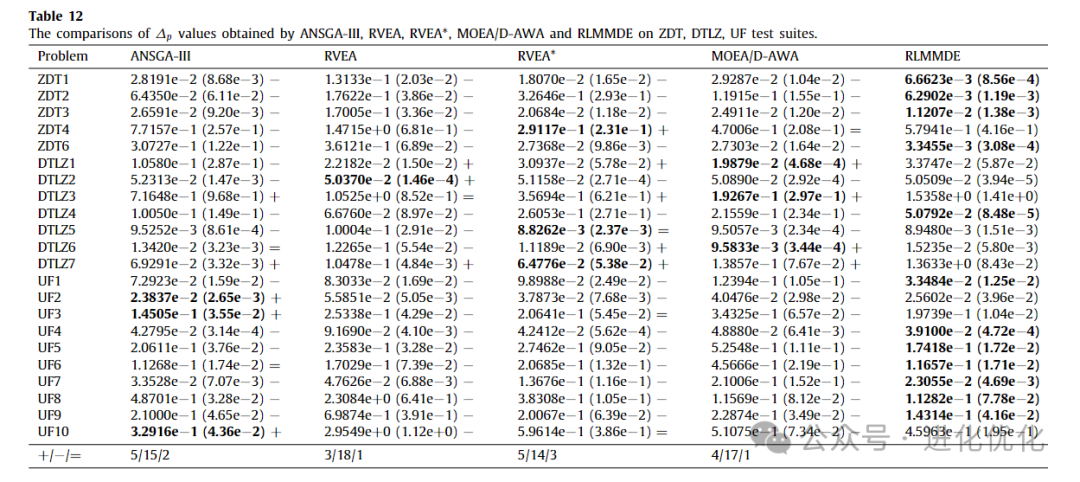
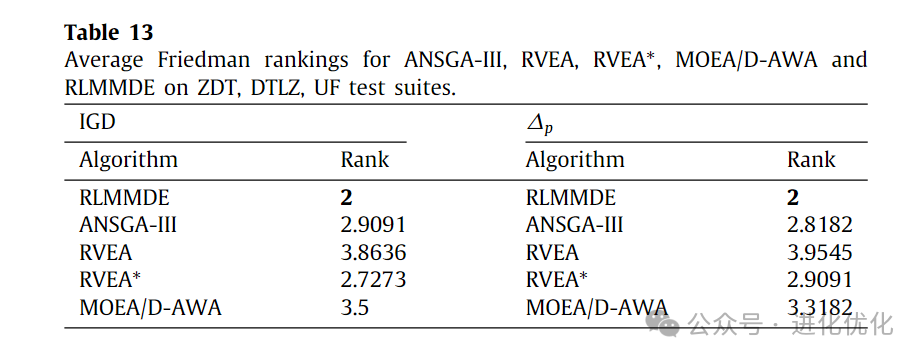
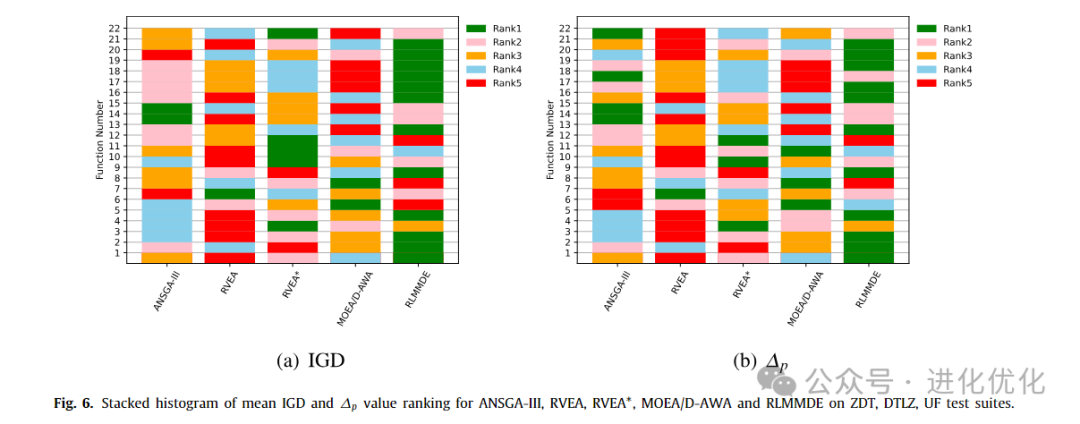
In this section, three MOEAs with reference point adaptation methods, namely ANSGA-III, RVEA, RVEA*, and MOEA/D-AWA, were compared with the proposed algorithm across three different types of test suites. Tables 11 and 12 provide detailed test results. As shown in Table 11, the performance of RLMMDE significantly outperforms the other 4 comparison algorithms. On these 22 test problems, RLMMDE obtained 12 optimal solutions, while the other algorithms obtained 1, 1, 5, and 2 optimal solutions, respectively. As shown in Table 12, for the experimental results of the ∆p metric, RLMMDE obtained 12 optimal solutions, while the other algorithms (from left to right in the table) obtained 3, 1, 3, and 3 optimal solutions on these 22 test problems. From the last row of the table, it can be seen that RLMMDE has at least 14 better results than other comparison algorithms. Additionally, to further demonstrate the experimental results of RLMMDE and the four comparison algorithms on the 22 test problems, Table 13 and Figure 6 show the average rankings after the Friedman test and the stacked histogram of IGD and ∆p rankings. From Table 13, it can be seen that RLMMDE achieved the best ranking in both IGD and ∆p values. From Figure 6, it can be seen that RLMMDE has the most green blocks, indicating that it achieved the best results and has the best performance. Finally, in terms of average ranking, average IGD, and ∆p value rankings, the proposed RLMMDE is more competitive among the comparison algorithms.
4.4 Performance Comparison with Other Test Instances
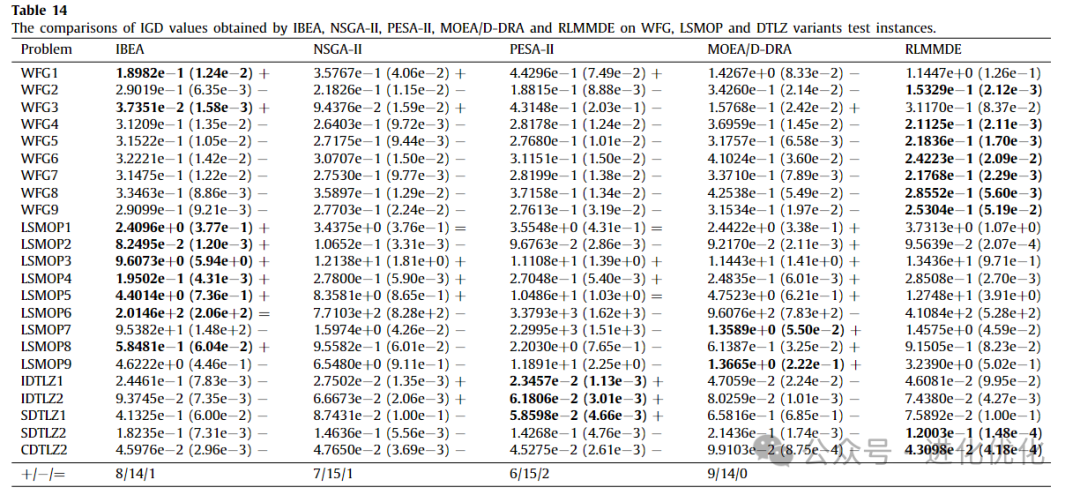
To further evaluate the performance of RLMMDE, comparisons were made with four classic MOEAs, namely NSGA-II, PESA-II, IBEA, and MOEA/DDRA, across the WFG, LSMOP, SDTLZ1, SDTLZ2, CDTLZ2, IDTLZ1, and IDTLZ2 test instances. Table 14 provides detailed test results. The table presents the IGD values obtained by RLMMDE and these comparison algorithms. As shown in Table 14, in the experimental results of the IGD metric, RLMMDE’s performance significantly outperforms the other four comparison algorithms. On these 23 test problems, RLMMDE obtained 9 optimal solutions, while the other algorithms obtained 9, 0, 3, and 2 optimal solutions, respectively. It is noteworthy that the proposed algorithm performs better on the WFG test suite but relatively poorly on the LSMOP test suite.

5

Summary and Outlook
5.1 Summary
This paper proposes a Reinforcement Learning-based Multi-Strategy Multi-Objective Differential Evolution Algorithm (RLMMDE). In RLMMDE, a multi-strategy multi-crossover DE optimizer is proposed to better balance exploration and exploitation, improving the algorithm’s performance in solving MOPs. To control the frequency of the reference point adaptive method, a reinforcement learning-based activation mechanism is proposed. Additionally, a reference point adaptive method is introduced to further enhance the algorithm’s performance in solving irregular Pareto front problems. In the experimental study, three different types of test suites were used to test the performance of RLMMDE. Compared to 9 traditional MOEAs, 3 MOEAs with different optimizers, and 4 MOEAs with reference point adaptation methods, the proposed algorithm demonstrates significant competitiveness. However, the feedback from the activation mechanism is sometimes not timely. The performance may degrade when processing certain issues after executing the reference point adaptive method. In the future, we will focus more on monitoring the state of the adjusted reference points and propose a reference point adaptive method with better problem universality.



Authors: Han Y, Peng H, Mei C, et al. Multi-strategy multi-objective differential evolutionary algorithm with reinforcement learning[J]. Knowledge-Based Systems, 2023, 277: 110801.



Editor: Wei Xinping
Illustration: Wei Xinping
Click the blue text to follow us