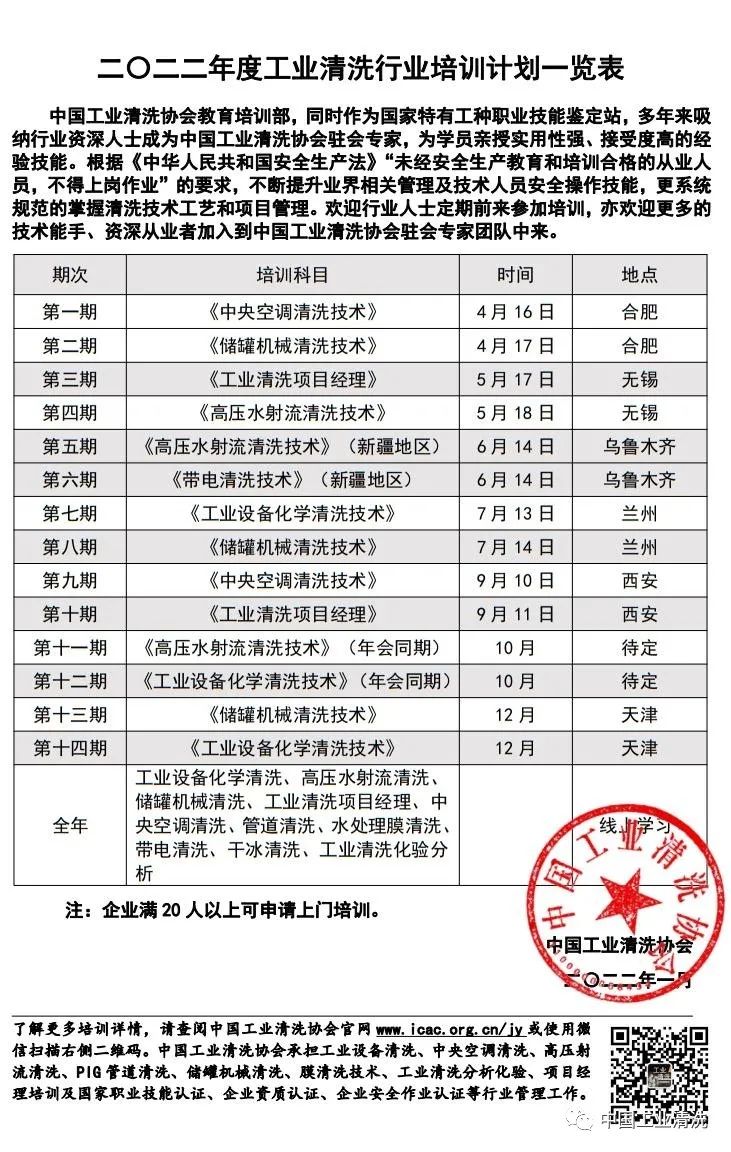
Part One
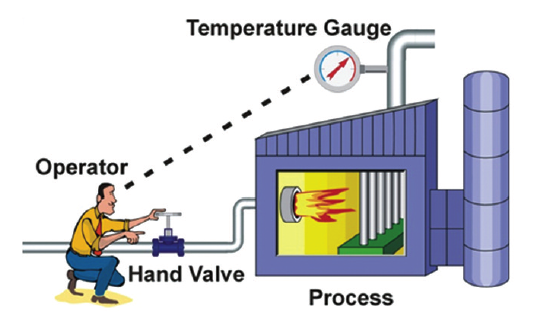
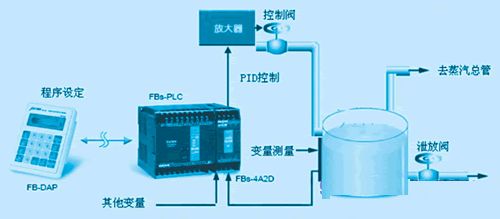
 .
. .
.
-
It can bring the physical quantity that needs to be controlled close to the target.
-
It can “anticipate” the trend of this quantity’s change.
-
It can also eliminate static errors caused by heat dissipation, resistance, and other factors.
-
….
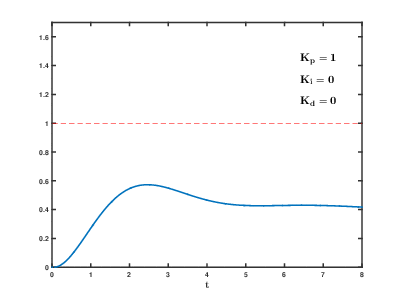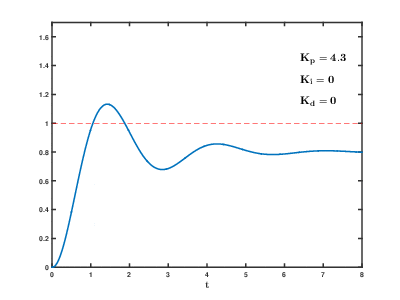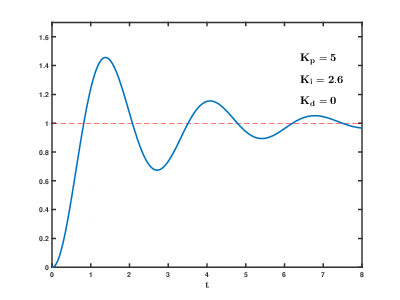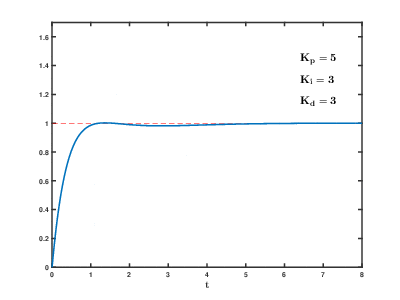
-
When the two values are not far apart, let the heater “gently heat a bit.
-
If, for some reason, the temperature drops significantly, let the heater “apply a little more force to heat.
-
If the current temperature is much lower than the target temperature, let the heater “run at full power to quickly bring the water temperature close to the target.

 .
.-
P thinks: I am very close to the target, I just need to heat gently.
-
D thinks: The heating and heat dissipation are equal, the temperature is stable, I seem to not need to adjust anything.

Part Two
Xiao Ming received a task: there is a water tank that is leaking (and the leak rate may not be constant), requiring the water level to be maintained at a certain position. Once the water level is found to be below the required position, water must be added to the tank. After receiving the task, Xiao Ming kept watch by the tank. After a long time, he found it boring, so he went to the room to read a novel, checking the water level every 30 minutes. The water leaked too fast; every time Xiao Ming came to check, the water was almost gone, far from the required height. Xiao Ming changed to checking every 3 minutes, but the water hardly leaked each time he came, so he didn’t need to add water. Coming too frequently resulted in wasted effort. After several trials, he determined to check every 10 minutes. This checking time is called the sampling period. At first, Xiao Ming used a ladle to add water, but the faucet was over ten meters away from the tank, requiring several trips to add enough water. Then Xiao Ming changed to using a bucket, adding a full bucket each time, reducing the number of trips and speeding up the filling process. However, he overflowed the tank several times, accidentally wetting his shoes. Xiao Ming then thought, instead of using a ladle or bucket, he would use a basin. After a few tries, he found it just right; he didn’t need to run too many times and wouldn’t let the water overflow. The size of this water-adding tool is called the proportional coefficient. Xiao Ming also found that while the water wouldn’t overflow, sometimes it would exceed the required height significantly, still risking wetting his shoes. He thought of a solution: installing a funnel on the tank, so that when adding water, it wouldn’t go directly into the tank but into the funnel to let it add slowly. This solved the overflow problem, but the water-adding speed became slow, sometimes failing to keep up with the leak rate. So he tried changing different sizes of funnels to control the water-adding speed, and finally found a satisfactory funnel. The time of the funnel is called the integral time. Xiao Ming finally took a breath, but the task’s requirements suddenly tightened. The timeliness of water level control was greatly increased; once the water level dropped too low, the water must be immediately added to the required position without exceeding it too much, or he wouldn’t get paid. Xiao Ming was in trouble again! He finally thought of a solution: keeping a basin of spare water nearby, and once he noticed the water level was low, he would add a basin of water directly without going through the funnel, ensuring timeliness, but the water level sometimes exceeded the required amount. He then drilled a hole just above the required water level and connected a pipe to a lower spare bucket, allowing the excess water to leak out from the hole above. The speed of this water leaking out is called the derivative time.
Seeing several posts about sampling periods, I suddenly thought of this story. The analogy of differentiation might be a bit forced, but as long as it helps with understanding, that’s fine. Hehe, it’s entry-level; if it can help beginners understand PID, that would be sufficient. In the story, Xiao Ming’s experiments were done step by step independently, but in reality, the water-adding tools, funnel diameters, and overflow hole sizes all impact the water-adding speed and the size of the water level overshoot. After conducting the later experiments, he often had to revise the results of the earlier experiments. Two, control model: a person uses PID control to pour half a cup of water from a kettle into a cup marked with a scale and then stops; the set value is the half-cup scale of the cup; the actual value is the actual water volume in the cup; the output value is the amount poured from the kettle and the amount scooped out from the cup; the measurement sensor is the person’s eyes; the executing object is the person; the action being executed is pouring water; the reverse action is scooping water. 1. P Proportional control means that when the person sees that the water volume in the cup has not reached the half-cup scale, they pour a certain amount of water from the kettle into the cup, or if the water volume exceeds the scale, they scoop a certain amount out of the cup. This action may result in not reaching half a cup or exceeding half a cup, and then stopping. Explanation: P proportional control is the simplest control method. The output of its controller is proportional to the input error signal. When only proportional control is used, the system output has a steady-state error (Steady-state error). 2. PI Integral control means pouring a certain amount of water into the cup, and if the water volume does not reach the scale, keep pouring. Later, if the water volume exceeds half a cup, scoop some out, and repeatedly not enough, pour more, too much, scoop out until the water volume reaches the scale. Explanation: In integral I control, the output of the controller is proportional to the integral of the input error signal. For an automatic control system, if there is a steady-state error after reaching steady state, this control system is said to have a steady-state error or is referred to as a system with steady-state error (System with Steady-state Error). To eliminate steady-state errors, an “integral term” must be introduced into the controller. The integral term depends on the integral of the error over time, which increases as time goes on. Thus, even if the error is small, the integral term will increase over time, pushing the controller’s output to further reduce the steady-state error until it equals zero. Therefore, the proportional + integral (PI) controller can eliminate steady-state errors after entering the steady state. 3. PID Differential control means that a person looks at the distance between the water volume in the cup and the scale. When the difference is significant, they pour a large amount of water from the kettle. When they see the water volume approaching the scale, they reduce the amount poured, slowly approaching the scale until stopping at the cup’s scale. If they can accurately stop at the scale position, it is zero static error control; if they stop near the scale, it is static error control. Explanation: In differential control D, the output of the controller is proportional to the derivative of the input error signal (i.e., the rate of change of the error). In practical engineering, the most widely used control law for regulators is proportional, integral, and differential control, referred to as PID control, also known as PID regulation. The PID controller has been in existence for nearly 70 years, and it has become one of the main technologies in industrial control due to its simple structure, good stability, reliable operation, and ease of adjustment. When the structure and parameters of the controlled object cannot be fully mastered or precise mathematical models cannot be obtained, and when other control theory techniques are difficult to apply, the structure and parameters of the system controller must be determined based on experience and on-site debugging. In this case, PID control technology is the most convenient. That is, when we do not fully understand a system and the controlled object, or cannot obtain system parameters through effective measurement methods, PID control technology is the most suitable. PID control, in practice, also includes PI and PD control. The PID controller calculates the control quantity based on the system’s error, utilizing proportional, integral, and differential calculations for control.
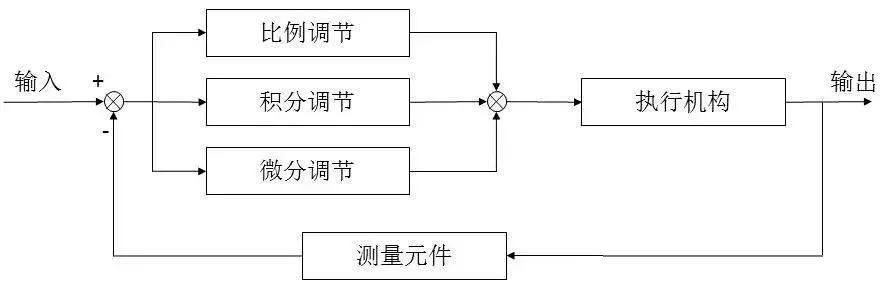
1. Proportional (P) Control
Proportional control is the simplest control method. Its controller output is proportional to the input error signal. When only proportional control is used, the system output has a steady-state error (Steady-state error).
2. Integral (I) Control
In integral control, the controller output is proportional to the integral of the input error signal. For an automatic control system, if there is a steady-state error after reaching steady state, this control system is said to have a steady-state error or is referred to as a system with steady-state error (System with Steady-state Error). To eliminate steady-state errors, an “integral term” must be introduced into the controller. The integral term depends on the integral of the error over time, which increases as time goes on. Thus, even if the error is small, the integral term will increase over time, pushing the controller’s output to further reduce the steady-state error until it equals zero. Therefore, the proportional + integral (PI) controller can eliminate steady-state errors after entering the steady state.
3. Differential (D) Control
In differential control, the controller output is proportional to the derivative of the input error signal (i.e., the rate of change of the error). Automatic control systems may experience oscillations or instability during the error correction process. This is due to the presence of large inertia components (links) or delay components that suppress the error, causing changes to lag behind the error changes. The solution is to make the change in the error suppression action “lead”; that is, when the error approaches zero, the error suppression action should also be zero. This means that simply introducing the “proportional” term into the controller is often not enough. The role of the proportional term is merely to amplify the magnitude of the error, while the current need is to add the “differential” term, which can predict the trend of error changes. Thus, a controller with proportional + differential can make the error suppression control action equal to zero in advance, or even negative, thereby avoiding severe overshoot of the controlled quantity. Therefore, for controlled objects with significant inertia or delays, a proportional + differential (PD) controller can improve the dynamic characteristics during the adjustment process.
When tuning PID parameters, it is ideal to have theoretical methods to determine PID parameters; however, in practical applications, it is more common to determine PID parameters through trial and error.
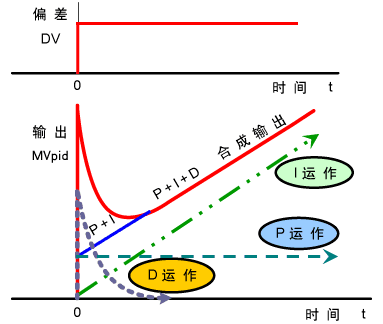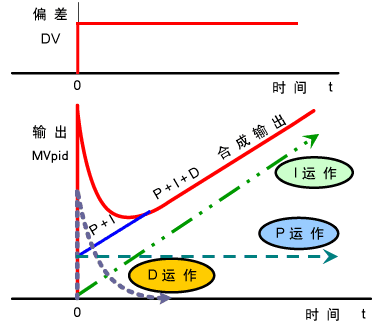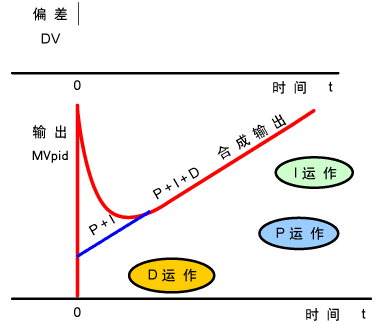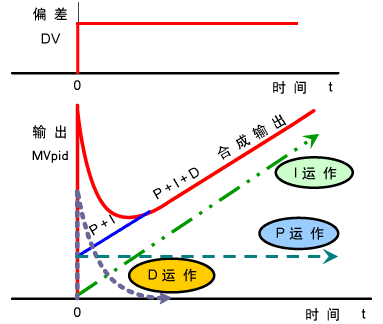
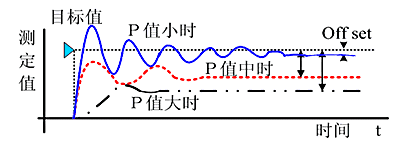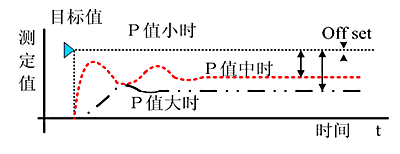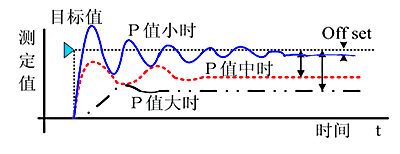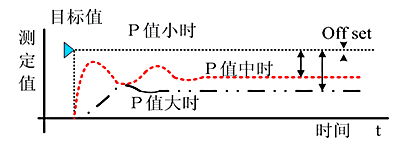
Increasing the proportional coefficient P generally speeds up the system’s response and is beneficial in reducing static errors in cases of steady-state error. However, too large a proportional coefficient can lead to significant overshoot and oscillations, degrading stability.
Increasing the integral time I helps reduce overshoot and oscillations, thus increasing the system’s stability, but it prolongs the time to eliminate static errors.
Increasing the differential time D is beneficial in accelerating the system’s response speed, reducing the overshoot, and enhancing stability, but it weakens the system’s ability to suppress disturbances.
During trial and error, one can refer to the above parameters’ trends on the system control process and adjust the parameters in the order of first proportional, then integral, and finally differential.
The tuning of PID controller parameters is the core content of control system design. It determines the sizes of the proportional coefficient, integral time, and differential time based on the characteristics of the controlled process. There are many methods for tuning PID controller parameters, which can be broadly categorized into two types:
1. Theoretical Calculation Tuning Method
This method primarily relies on the mathematical model of the system, determining controller parameters through theoretical calculations. The calculated data obtained from this method may not be directly usable and must be adjusted and modified through engineering practice.
2. Engineering Tuning Method
This method primarily relies on engineering experience, directly conducting experiments in the control system, and is widely adopted in engineering practice due to its simplicity and ease of mastery. The engineering tuning methods for PID controller parameters mainly include the critical ratio method, reaction curve method, and decay method. Each method has its characteristics, and their commonality is that they all rely on experiments and then adjust controller parameters according to engineering experience formulas. However, regardless of which method is used to obtain controller parameters, final adjustments and improvements must be made during actual operation.
Currently, the critical ratio method is generally employed. The steps for tuning PID controller parameters using this method are as follows:
(1) First, pre-select a sufficiently short sampling period for the system to operate;
(2) Only add the proportional control element until the system exhibits critical oscillation in response to the input step, recording the proportional gain and the critical oscillation period at that time;
(3) Calculate the PID controller parameters using formulas under certain control levels.
The setting of PID parameters relies on experience and familiarity with the process, referring to the measurement values tracking the set value curve to adjust the sizes of P, I, and D.
Common Mnemonics:
Finding the best parameters for tuning, checking in order from small to large;
First is proportional, then integral, and finally add differential;
If the curve oscillates frequently, enlarge the proportional dial;
If the curve drifts around a large bay, reduce the proportional dial;
If the curve deviates slowly, reduce the integral time;
If the curve oscillates with a long period, increase the integral time;
Step one: Tuning Proportional Control
Gradually increase the proportional control effect, observing each response until a quick reaction with small overshoot is obtained.
Step two: Tuning the Integral Element
If the steady-state error cannot meet the requirements under proportional control, integral control must be added. First, reduce the proportional coefficient selected in the previous step to 50-80% of its original value, and set the integral time to a larger value, observing the response curve. Then, reduce the integral time, increase the integral effect, and adjust the proportional coefficient accordingly, repeating this process until a satisfactory response is achieved, confirming the parameters for proportional and integral.
Step three: Tuning the Differential Element
If after the above steps, PI control can only eliminate steady-state errors but the dynamic process is unsatisfactory, differential control should be added to form PID control. Start with the differential time TD=0, gradually increase TD while adjusting the proportional coefficient and integral time accordingly, repeating this process until satisfactory control effects and PID control parameters are obtained.
Without the right tools, one cannot undertake delicate tasks. To master and apply PID, it is essential to learn the basic concepts to arm ourselves; some concepts will be accompanied by commonly used representations in practical engineering, starting with “Actual:”.
1. Controlled Quantity: The value reflecting the actual fluctuations of the controlled object. The controlled quantity changes frequently.
Actual: Common detection feedback values, such as yout(t).
2. Set Value: The set value of the PID regulator is the value that people expect the controlled quantity to reach. The set value can be fixed or variable.
Actual: Manually set, often represented as rin(t).
3. Control Output: The output of the PID regulator, which is the instruction sent to the external execution structure to act according to its requirements based on the changes in the controlled quantity. Note the distinction from the controlled quantity yout(t); these two concepts are entirely different and are often confused.
Actual: The formula you often see, “u(t)=kp[e(t)+1/TI∫e(t)dt+TD*de(t)/dt]”, where u(t) is represented.
4. Input Deviation: The difference between the controlled quantity and the set value.
Actual: error(t)=rin(t)-yout(t).
5. P (Proportional): P is the proportional action, simply put, it is the input deviation multiplied by a coefficient.
Actual: For example, kp, KP are the same.
6. I (Integral): I is the integral, simply put, it is the integral operation of the input deviation.
Actual: For example, ki.
7. D (Derivative): D is the derivative, simply put, it is the derivative operation of the input deviation.
Actual: For example, kd.
8. Basic PID Formula: The tuning process of the PID regulator can be simply stated as first adjusting the system to pure proportional action, gradually strengthening the proportional action to produce equal amplitude oscillations, recording the proportional action and oscillation period, then multiplying this proportional action by 0.6, and appropriately extending the integral action.
KP= 0.6*Km
KD= KP*π/4ω or KD= KP*tu/8
KI= KP*ω/π or KI= 2KP/tu
KP: Proportional control parameter;
KD: Integral control parameter;
KI: Derivative control parameter;
Km: The proportional value at which the system begins to oscillate, usually referred to as the critical proportional value;
ω: The frequency during equal amplitude oscillation, where tu is the oscillation period. Here tuω =2π, not tuω=1. Those who have studied Fourier and Laplace transforms should understand why this is the case; we will not delve into it here.
9. Single Loop: A single loop is a PID control system with only one PID.
10. Cascade: When one PID is not enough, cascade means connecting two PID controllers together to form a cascade control system, also called a double-loop control system. In a cascade control system, the PID regulator has a main control and a sub-control distinction.
In a cascade control system, the PID that regulates the controlled quantity is called the main control, and the PID that directly commands the actuator is called the sub-control. The control output of the main control enters the sub-control as the set value. The main control uses a single-loop PID regulator, while the sub-control uses an externally given regulator.
11. Positive Action
For the PID regulator, the control output increases as the controlled quantity increases and decreases as the controlled quantity decreases, which is called positive action.
12. Negative Action
For the PID regulator, the control output decreases as the controlled quantity increases and increases as the controlled quantity decreases, which is called negative action.
13. Dynamic Deviation
During the adjustment process, the deviation between the controlled quantity and the set value changes at any time; the deviation between the two at any moment is called dynamic deviation.
14. Static Deviation
After the adjustment stabilizes, the deviation between the controlled quantity and the set value that still exists is called static deviation. Eliminating static deviation is achieved through the integral action of the PID regulator.
15. Callback
The adjustment action shows that the controlled quantity begins to change from rising to falling or from falling to rising, which is called callback.
Disclaimer: The content is sourced from the internet, WeChat public accounts, and other public channels. We maintain neutrality regarding the viewpoints expressed herein and provide it for reference and communication purposes. The copyright of the reprinted manuscripts belongs to the original authors and institutions. If there is any infringement, please contact us for deletion.
|
|


For training registration and more content, please scan the above QR code.
Visit the official website of the China Industrial Cleaning Association.