
In 1993, game development company id Software released the first-person shooter game DOOM, which quickly became a sensation. Today, DOOM is considered one of the most influential games of all time.
Ten years after the release of DOOM (in 2003), journalist David Kushner published a book about id Software titled Masters of Doom, which has since been regarded as a definitive account of the game’s creation history. I read this book a few years ago, and while my memory of its contents is somewhat hazy now, there is one story about id Software’s chief programmer John Carmack that stands out vividly. I will provide a brief description of the story here (for more details, please read on). In fact, early in the development of DOOM, Carmack found that the 3D renderer he was writing for the game was as slow as molasses when rendering certain levels. For a fast-paced shooting game like DOOM, which has high demands for dynamism and speed, this was a serious issue. Realizing the gravity of the situation, Carmack needed a more efficient rendering algorithm, so he began reading relevant papers. Ultimately, he implemented a technique called binary space partitioning (BSP), which greatly improved the performance of the DOOM game engine, and this technique had never been used in video games before.
I have always found this story to be particularly striking. Carmack applied cutting-edge academic research to video games, and I believe this is a significant reason why he became a legendary figure. From any angle, Carmack should be recognized as a quintessential genius programmer in the video game industry, and this story is one of the first reasons that come to my mind.
Clearly, the term “binary space partitioning” sounds like a highly complex topic, and being able to read papers on it and put it into practice is no small feat, which is why this story left a deep impression on me. I have always thought that Carmack’s approach was highly innovative, but since I neither understand what binary space partitioning is nor know how revolutionary this technology was at the time, I am not certain whether my opinion is correct. If we were to rank geniuses from Homer Simpson (the father from The Simpsons) to Albert Einstein, where would Carmack’s application of binary space partitioning in DOOM fit in?
At the same time, I am curious about where the concept of binary space partitioning originated and how it caught Carmack’s attention. Therefore, this article will not only recount the story of John Carmack and DOOM, but also explore the historical development of the binary space partitioning tree (BSP tree) data structure. Interestingly, like many other technologies in computer science, the BSP tree initially originated from military research.
Indeed, the first level of DOOM, E1M1, was inspired by the United States Air Force.
VSD Problem
The BSP tree is one of the solutions to the most challenging problems in computer graphics. For example, in order to render a 3D scene, the renderer must be able to distinguish between visible and invisible objects from a specific viewpoint. If there is ample rendering time, this requirement isn’t a big problem; however, ideally, a real-time game engine needs to complete at least 30 such distinction tasks per second.
This problem is sometimes referred to as the visible surface determination (VSD) problem. Later, programmer Michael Abrash, who collaborated with Carmack on the development of Quake (the game developed by id Software after DOOM), wrote in his book Graphics Programming Black Book:
I want to discuss what I consider to be one of the most difficult problems in 3D: the visible surface determination problem (drawing the appropriate surface at each pixel) and the closely related hidden surface elimination problem (quickly removing invisible polygons to speed up visible surface detection). For brevity, I will use the abbreviation VSD to refer to visible surface determination and hidden surface elimination.
Why do I consider VSD to be the most challenging problem in 3D? Although rasterization problems like texture mapping are more interesting and important, they are relatively limited tasks. With the advent of 3D accelerators, they have gradually been offloaded to hardware. Additionally, they only increase with the screen resolution, and the increase in resolution is relatively moderate.
In contrast, VSD is like a bottomless pit, and there are many solutions available. However, when using simple methods to handle VSD, performance is directly affected by the complexity of the scene, which typically increases quadratically or cubically. Therefore, during rendering, VSD quickly becomes a limiting factor.[1]
Abrash wrote about the difficulties of the VSD problem in the late 1990s, several years after DOOM, which proved that ordinary people longed to play graphically intensive games on their own computers. In the early 1990s, id Software released several games after its establishment. Although computers at the time were primarily used for text and spreadsheet processing or other tasks, no one had considered running games on them. Id Software had to program the games they released to run smoothly on computers. To achieve this leap, especially to ensure that the few 3D games released by id Software before DOOM could run on computers, id Software had to innovate. In these games, all levels were designed with certain limitations to make it easier to solve the VSD problem.
For example, before DOOM, id Software released Wolfenstein 3D, where every level was composed of walls aligned with the coordinate axes. In other words, in the graphics of Wolfenstein 3D, you only saw walls oriented north-south or east-west. In the game, there were fixed gaps between walls, and all corridors were either one square or two squares wide, but never 2.5 squares. As a result, although the id Software team could only design levels that looked very similar, it made Carmack’s task of writing a renderer for Wolfenstein 3D much easier.
By casting rays on the screen into the virtual game world, the renderer of Wolfenstein 3D solved the VSD problem. Generally, a renderer that uses rays is called a “ray casting” renderer. This type of renderer is usually slow because solving the internal VSD problem involves finding the first intersection point between rays and objects in the game, which often requires a lot of computation. However, in Wolfenstein 3D, since all walls were aligned with the grid, the intersection points of rays with walls could only occur at grid lines. Thus, the renderer only needed to check these intersection points one by one. If the renderer started checking from the intersection point closest to the player’s viewpoint and continued to the next closest point, stopping when it encountered the first wall, the VSD problem would be easily solved. Rays would be cast from each pixel forward, stopping when they intersected with objects on the screen; this method was feasible. From a CPU resource perspective, the casting cost was low. In fact, since all walls were of the same height, a single ray only needed to be cast for pixels in the same column.
Despite the absence of specialized graphics cards at the time, Wolfenstein 3D managed to run smoothly on low-spec personal computers due to this clever approach. However, this method was not suitable for DOOM. Because id Software added many new elements to this new game—slanted walls, stairs, and varying ceiling heights—ray casting was no longer applicable, so Carmack wrote a new renderer. The renderer for Wolfenstein 3D focused on images, casting rays onto the columns represented by screen pixels, while the renderer for DOOM focused on objects. In other words, the DOOM renderer would record all objects in the game scene and then project them onto the screen, rather than recording the pixels on the screen and determining the color of each pixel.
For an object-focused renderer, using a Z-buffer to solve the VSD problem was relatively straightforward. Each time an object was projected onto the screen, the renderer needed to check each pixel being drawn. If the part of the object you wanted to draw was closer to the player than the object already drawn on the target pixel, it would overwrite it. Otherwise, the pixel would remain unchanged. Although this method is simple, the Z-buffer requires a lot of memory, and the renderer may still spend substantial CPU resources projecting geometries that the player will never see.
In the 1990s, the Z-buffer method also had other drawbacks: IBM-compatible PCs were equipped with a display adapter system called VGA, which made writing images to the frame buffer very costly. Therefore, spending time drawing pixels that would only be overwritten later slowed down the renderer’s performance.
Given the high cost of writing images to the frame buffer, an ideal renderer would need to draw the closest objects to the player first, followed by the next closest, and so on, until every pixel on the screen was filled with information. At this point, the renderer would stop, significantly reducing the rendering time for objects that were not visible in the distance. This method of sorting objects from nearest to farthest could also solve the VSD problem. The question then arises: what can the player see?
Initially, Carmack intended to rely on the level layout of DOOM to solve the VSD problem. First, the renderer would draw the walls of the room the player was currently in, and then when the player rushed into the adjacent room, it would draw the walls of that room. Since each room did not occlude each other, this method could also solve the VSD problem. Rooms that occluded each other could be divided into several non-occluding “regions”. In a video on YouTube, Bisqwit demonstrated a renderer he created using the same algorithm. You can see the rendering process if you run it at a super slow speed. This algorithm was also applied in Duke Nukem 3D, which was released three years after DOOM, when CPU performance had also improved significantly. In 1993, although hardware was already capable of running games, the renderer of DOOM still struggled with complex hierarchical structures, especially when parts of rooms were nested within each other. Unfortunately, this type of hierarchical structure was the only way to construct spiral staircases and similar objects. Walking down a spiral staircase until entering an already rendered area involved multiple cycles of descending movement, which significantly slowed down the game’s engine performance.
When the id Software team realized that the speed of the DOOM game engine might be too slow, the company faced another task: porting Wolfenstein 3D to the Super Nintendo Entertainment System (SNES). At that time, the SNES’s performance was worse than that of IBM-compatible PCs. The results showed that although the ray casting renderer was very simple, it was impossible to run it quickly on the SNES. Thus, Carmack began researching more efficient algorithms. In fact, it was to successfully port Wolfenstein 3D to the SNES that Carmack first studied the binary space partitioning technique and applied it. Since the walls of Wolfenstein 3D were aligned with the coordinate axes, applying the binary space partitioning technique was straightforward; however, DOOM was more complex. Nevertheless, Carmack discovered that the binary space partitioning tree could also be used to solve the speed issues of DOOM.
Binary Space Partitioning
Binary space partitioning (BSP) divides the 3D scene into several parts in advance, making the VSD problem easier to solve. At this point, you need to understand why partitioning the scene can be effective: if you draw a line on the scene (corresponding to a plane in three-dimensional space), you can indicate which side of the line the player or camera’s viewpoint is on; objects on the other side of the line cannot occlude objects on the side where the player is located. If you repeat this operation multiple times, the three-dimensional scene will eventually be divided into multiple regions; this is not an improvement to the original scene, but now you know more about how different parts of the scene will occlude each other.
The concept of partitioning a three-dimensional scene was first articulated by researchers from the United States Air Force, who attempted to prove to the Air Force that computer graphics had advanced enough to be applied to flight simulators. In 1969, they published their findings in a report titled “A Study for Applying Computer-Generated Images to Visual Simulation”. The summary section of the report noted that computer graphics could be used to train pilots, but also warned that practical applications might be limited by the VSD problem:
A key issue that real-time image processing needs to solve is the priority problem, or hidden line problem. When we observe the outside world with our eyes, nature easily solves this problem for us: a point on an opaque object occludes all other objects that are farther away in the same visual direction. However, this task is very difficult in computers. The priority problem that image processing needs to solve increases exponentially with the complexity of the environment, quickly exceeding the computational load required to draw the perspective of the objects.[2]
They proposed a solution based on constructing an “occlusion matrix,” which was reportedly used in earlier NASA projects. The researchers pointed out that a plane could divide the scene into two, which could be used to resolve any priority issues between objects on either side of the plane. Typically, these planes would need to be explicitly added to the scene, but for certain geometries, you could simply use the surfaces of the geometries you already had. They provided an example: p1, p2, and p3 are three different planes, and if the camera’s viewpoint is in front of one of the planes, i.e., the “front” side, the value of pi equals 1. This matrix illustrates the relationships between three objects based on three different planes and the camera’s viewpoint position—if object ai occludes object aj, then aij in this matrix equals 1.
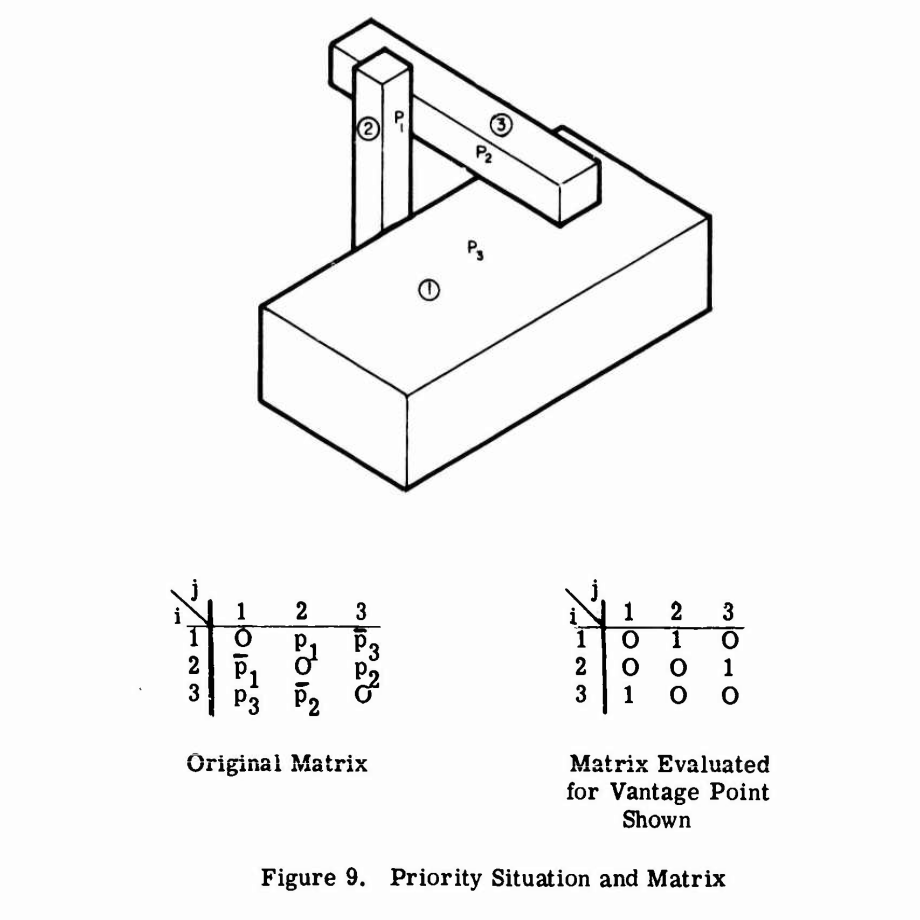
The researchers noted that this matrix could be applied to hardware and re-evaluated for each frame. The matrix essentially serves as a large switch or a preset Z-buffer. When drawing a given object, if the value in the column of the object is 1 and the row is already being drawn, the occluded parts of the object will not be rendered.
However, the main drawback of the matrix method is that to represent n objects in the scene, you need a matrix of size n2. Thus, the researchers continued to delve deeper, exploring the feasibility of representing the occlusion matrix as a “priority list,” which has a size of n and can determine the order in which objects are drawn. They soon discovered that scenes like the one shown above could not determine an order (due to cyclic blocking). Therefore, they spent considerable time clarifying the mathematical distinctions between “suitable” and “unsuitable” scenes. Ultimately, they concluded that at least for “suitable” scenes, a priority list could be created; and for scene designers, avoiding the design of “unsuitable” scenes is not particularly difficult. However, they did not specify how to generate this list. It can be said that the primary contribution of this 1969 study was the assertion that at least, in theory, the method of plane partitioning could be used to sort objects for rendering in the scene.
By 1980, a paper titled “Visible Surface Generation by A Priori Tree Structures” proposed specific algorithms to solve this problem. In this paper, authors Henry Fuchs, Zvi Kedem, and Bruce Naylor introduced the BSP tree. They pointed out that this new data structure “can replace a solution that was first used ten years ago but did not gain widespread development due to various issues” (i.e., the solution from the 1969 Air Force-related study mentioned earlier).[3] Once a BSP tree is generated, it can be used to determine the order of priority for objects in the scene.
The three authors provided a fairly readable explanation of how the BSP tree works in their paper. However, in this article, I will attempt to explain it in simpler terms.
First, select a polygon in the scene and use the plane of that polygon as the splitting plane. This polygon acts as the root node of the tree. The remaining polygons in the scene will be distributed on either side of the splitting plane. Polygons that are “in front of” the splitting surface or intersect with it and are in the “front” half will fall into the left subtree of the root node; those that are “behind” the splitting surface or intersect with it and are in the “back” half will fall into the right subtree. Then, this process is recursively repeated: a polygon is selected in both the left and right subtrees as the new splitting plane, further subdividing the space and creating new subtrees. Once all polygons are selected, the binary space partitioning process is complete.
Suppose you want to render the geometries in the scene from back to front (this is known as the “painter’s algorithm”). As you draw, polygons that are farther from the camera will be covered by those that are closer to the camera, thus correctly performing the rendering task. To implement this algorithm, you must traverse the BSP tree in order, with the rendering order of the left and right subtrees determined by the relationship between the camera’s viewpoint and the position of the node’s splitting plane. Therefore, for each node on the tree, first render all polygons on the side of the splitting plane that is “farther away,” then the polygons on the plane itself, and finally the polygons on the side that is “closer”—”farther” and “closer” relative to the camera’s viewpoint. As explained earlier, polygons on the side that is farther from the splitting plane cannot occlude objects on the nearer side, so this method can solve the VSD problem.
The following image illustrates the construction and traversal process of a BSP tree for a simple two-dimensional scene. In two dimensions, the splitting plane becomes a splitting line, but conceptually, it is no different from complex three-dimensional scenes.
Step 1: The root splitting line falls on wall D, dividing the remaining geometries into two groups.
Step 2: Continue to split the spaces on either side of wall D. Wall C is the only wall on one side, so no further splitting is needed. On the other side, wall B forms a new splitting plane. Since wall A intersects with the new splitting plane, it must be split into two walls.
Step 3: Referencing the upper right perspective, sort the walls from back to front, which is helpful for executing the painter’s algorithm. This is the order traversal process of the tree.
Fuchs, Kedem, and Naylor emphasized the advantages of the BSP tree: it only needs to be constructed once. It may be hard to believe, but in reality, regardless of where the camera’s viewpoint is, the same BSP tree can be used to render a scene. As long as the polygons in the scene do not move, the BSP tree remains valid. Therefore, the BSP tree is very practical for real-time rendering tasks— all the arduous tasks of constructing the tree can be completed before rendering begins.
At the same time, the three also mentioned a question that requires further research: how can we construct a “high-quality” BSP tree? The quality of a BSP tree depends on the choice of polygons used as splitting planes. I skipped this question earlier, but if the polygon used as the splitting plane intersects with other polygons, then to make the BSP algorithm work, the intersecting polygon must be split in two, so that the two parts can be placed in different spaces. However, if this phenomenon occurs repeatedly, the construction of the BSP tree will significantly increase the number of polygons in the scene.
Naylor later mentioned this issue in his 1993 paper “Constructing High-Quality Split Trees.” Carmack’s colleague and co-founder of id Software John Romero pointed out that this paper was one of the ones Carmack read when introducing BSP trees in DOOM.[4]
BSP Trees in DOOM
Don’t forget that when Carmack first designed the renderer for DOOM, he tried to establish a rendering order for the level geometry by having the renderer render the adjacent rooms outside the player’s current room. The BSP tree was an excellent choice for this, as it could prevent the renderer from doing redundant work when the player entered previous rooms (regions), thus saving CPU resources.
In fact, “introducing the BSP tree into DOOM” meant incorporating the BSP tree generator into the level editor of DOOM. When completing the production of a DOOM level, the BSP tree would be generated based on the level geometry. According to programmer Fabien Sanglard, it took 8 seconds to generate the BSP tree for one level in the original DOOM, and a total of 11 minutes for all levels [5]. The reason for the long generation time was partly due to the BSP generation algorithm used by Carmack, which attempted to use various heuristic methods to find a “high-quality” BSP tree. An 8-second delay at runtime may be unacceptable; however, offline, 8 seconds is not long, especially considering that the BSP tree improved the renderer’s performance. The BSP tree generated for each level would be loaded as level data when the game started.
Carmack modified the BSP tree algorithm proposed in the 1980 paper because, when DOOM starts running, the BSP tree for the current level is read into memory, and the renderer draws objects from front to back using the BSP tree, rather than back to front. The three authors demonstrated that the BSP tree could be used to execute the back-to-front painter’s algorithm, but the painter’s algorithm would cause many redundant drawing tasks, which would be burdensome for IBM-compatible PCs. Therefore, the renderer for DOOM reversed the order, first drawing the geometries closest to the player, and then those farther away. This reverse sorting could be easily implemented using the BSP tree because you could traverse each node of the tree in reverse order. To prevent the far-away geometries from occluding the nearer ones, the renderer of DOOM used an implicit Z-buffer, which not only had the advantages of a regular Z-buffer but also required less memory. This Z-buffer had two arrays, one recording horizontal occlusion relationships and two others recording vertical occlusion relationships from the top and bottom of the screen. The renderer of DOOM could function without using an actual Z-buffer because, technically speaking, it wasn’t a true 3D game. The cost of the BSP tree data structure was low, but it could still work because DOOM did not encounter the following issues: the horizontal occlusion array worked because there were no slanted walls in the game; the vertical occlusion array worked because there were no walls with two windows at different heights.
The remaining tricky problem was how to incorporate moving characters in DOOM into the static level geometry rendered using the BSP tree. The enemies in the game could not be included in the BSP tree because they moved, while the BSP tree only worked for static geometries. Therefore, the renderer first drew the static level geometries while collaborating with another data structure that used memory more efficiently to record the areas on the screen designated for rendering. Then, the renderer drew the enemies in a back-to-front order and eliminated those that were occluded by the areas on the screen. This process was slightly less effective than rendering using the BSP tree. However, since the number of enemies visible in the level was less than the number of geometries, speed was not a significant issue.
Applying the BSP tree in DOOM was undoubtedly a great success. It was undoubtedly brilliant of Carmack to think of the BSP tree as the best solution to the VSD problem. But can this be called a genius move?
Sanglard cites Romero in his book about the DOOM game engine: Naylor’s paper on “Constructing High-Quality Split Trees” primarily discusses using BSP trees to eliminate the backs of 3D models.[6] According to Romero, Carmack believed that this algorithm was still effective for DOOM, so he gave it a try and applied the BSP technique to the game. However, this statement seems somewhat flattering—it implies that Carmack discovered that while others were still using BSP trees to render static scenes, he found that the technology could be applied to real-time gaming. There are also stories in Masters of Doom that praise Carmack. The author, Kushner, believes that after reading Naylor’s paper, Carmack asked himself, “What if we used BSP technology to create an entire virtual world, rather than just a 3D image?” [7].
These “one-sided remarks” overlook the historical development of the BSP tree. When researchers from the U.S. Air Force began to realize that scene partitioning could speed up rendering tasks, they were interested in improving real-time rendering speed, as they were trying to create a flight simulator. In 1980, the same case appeared again in Fuchs et al.’s paper, where they explored how BSP trees could be applied in flight simulators to help pilots train: pilots used it to repeatedly practice landing at the same airport. Since the terrain of the airport does not change, the BSP tree only needs to be generated once, making it a one-time effort. It is clear that they were considering real-time simulation. In the introduction of the paper, Fuchs et al. also discussed that real-time graphics systems must generate an image within at least 1/30 of a second, which motivated their research.
Thus, Carmack was not the first to think of applying BSP trees in real-time graphics simulation. Indeed, envisioning and putting ideas into practice are two different things. However, even during the implementation process, Carmack received far more help and guidance than people might imagine. As of the time of writing this article, the BSP tree Wikipedia page indicates that Carmack referenced a paper by Chen and Gordon from 1991, as well as a textbook titled Computer Graphics: Principles and Practice from 1990. Although the page does not provide citation information, its credibility is unquestionable. Chen and Gordon’s paper introduced a front-to-back rendering method using BSP trees, which is essentially consistent with the method used in DOOM, and also included what I refer to as the “implicit Z-buffer” data structure, which can prevent distant graphics from occluding nearer graphics during rendering. Computer Graphics: Principles and Practice thoroughly discusses BSP trees and provides pseudocode for constructing and displaying BSP trees (thanks to my university library for allowing me to view the 1990 edition of this textbook). Since this book is a classic in computer graphics, it is highly likely that Carmack had a copy.
However, Carmack found himself facing a new problem: how to make a first-person shooter game run on a computer that couldn’t even perform floating-point operations? Through investigation, he proved that the data structure of BSP trees is very suitable for real-time video game rendering. Although BSP trees had been proposed long ago and the relevant theories were well-developed by Carmack’s time, I still believe that what Carmack did was an astonishing feat. Perhaps what deserves praise is the entire DOOM game engine, which is indeed very sophisticated. I mentioned this earlier, but Sanglard’s Game Engine Black Book: DOOM explains the extraordinary nature of this game engine and how these advantages fit together. It is important to understand that the VSD problem was just one of many issues Carmack had to solve while writing the DOOM game engine. I must say that Carmack’s ability to consult relevant literature and put it into practice, facing complex data structures that are unknown to most programmers, speaks volumes about his technical prowess and unique craftsmanship.
If you liked this article, feel free to follow us on Twitter @TwoBitHistory, and you can subscribe via RSS feed for the latest articles (updated every four weeks).
via: https://twobithistory.org/2019/11/06/doom-bsp.html
Author: Two-Bit History | Editor: lujun9972 | Translator: aREversez | Proofreader: wxy
This article is an original translation by LCTT, honorably presented by Linux China.
|