The MSR algorithm is based on the Retinex theory and introduces the concept of multi-scale decomposition. Early Retinex (SSR) algorithms faced some issues in practical applications. For instance, they are sensitive to the brightness range of input images and may exhibit unstable performance under different lighting conditions and object types. Therefore, to further improve the performance and effectiveness of the Retinex algorithm, researchers proposed the Multi-Scale Retinex (MSR) algorithm.The core idea of the MSR algorithm is to process the image at different scales, which allows for better capture and handling of object details and lighting information. Through multi-scale decomposition and reconstruction, the MSR algorithm can enhance the contrast and details of the image while maintaining the true colors of the objects, and better adapt to different lighting conditions and object types.The operations in MSR are similar to those in SSR. Before reading this article, it is recommended to review the previous article on SSR, which introduces the principles and computational processes of SSR.After reviewing SSR, we understand that the core idea of the Retinex algorithm is to eliminate the influence of incident light to obtain the true colors and texture information of objects under different lighting conditions.The specific process in MSR is shown in the following equation:
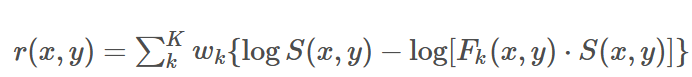
Where k is the number of Gaussian kernels. When k=1, MSR degenerates to SSR. Generally, to ensure that the advantages of SSR at high, medium, and low scales are considered, k is typically set to 3, with w1=w2=w3=1/3, and convolution kernel sizes of 15, 80, and 200 can yield good results.For MSR, to integrate the advantages of multiple scales, three different scales of Gaussian kernels are chosen for convolution operations, resulting in three different scale image components. The coarser scale component captures lower frequency lighting information, while the finer scale component captures higher frequency details. This allows for better image processing at different scales and integrates the advantages of different scale components. The weights of the three convolutions are evenly distributed among the different scale incident images, and during the addition process, the different scale image components are actually combined with weighted synthesis. This weighted synthesis considers the contributions of different scale components without giving excessive weight to any single scale. Through this method, a better balance of the influences of different scale components can be achieved, resulting in more accurate image enhancement outcomes. We believe that the weighted results can more closely approximate the incident effects on the image.
The final result r(x, y) is converted from the logarithmic domain to the real number domain, yielding the output image R(x, y).


Editor / Garvey
Reviewer / Wang Manzhen
Recheck / Sun Tianming
Click below
Follow us