LoRA-Dash: A More Efficient Method for Task-Specific Fine-Tuning

Article Link:

https://arxiv.org/abs/2409.01035

Code Link:

https://github.com/Chongjie-Si/Subspace-Tuning

Project Homepage:

https://chongjiesi.site/project/2024-lora-dash.html

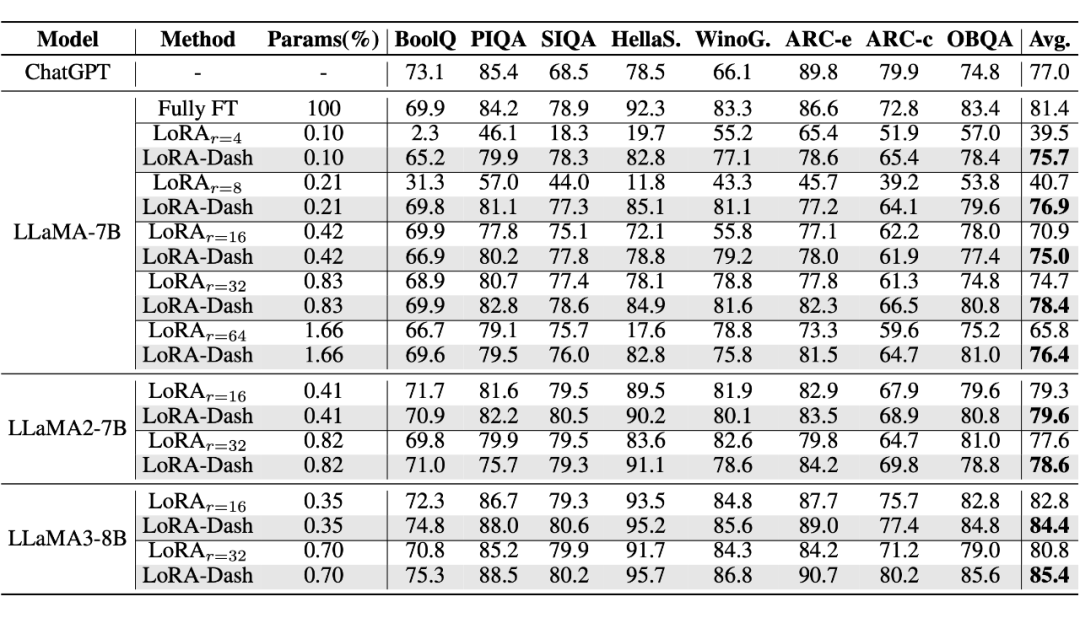
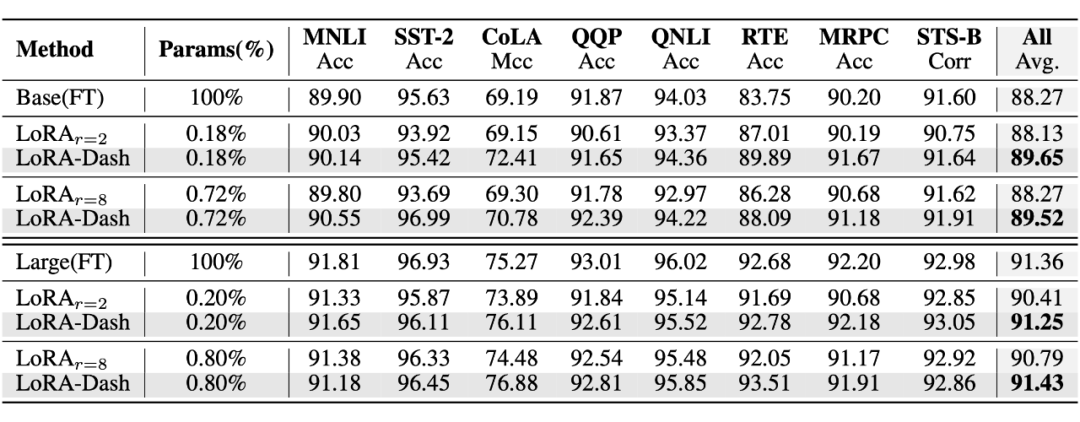
Due to the rich content of the LoRA-Dash paper, compressing 30 pages of content into 10 pages is a highly challenging task. Therefore, we have made careful trade-offs between readability and content integrity. The starting point of this article may differ from the original paper, aligning more closely with our initial motivations and goals.

Research Motivation

1.1 Top, Bottom, or Random?

LoRA needs no introduction, as it is one of the most well-known methods in the field of fine-tuning, with a wide impact. In previous research on related methods, I noticed several studies specifically discussing LoRA initialization:

• PISSA: suggests that the matrices A and B in LoRA initialization should correspond to the maximum singular value part of the weight matrix W.

• MiLORA: proposes that the A and B in LoRA initialization should reflect the minimum singular value part of W.

In addition, some methods suggest adjusting the maximum singular direction of the weight matrix W, such as Spectral Adapter, or randomly selecting singular directions for adjustment, like RoSA. In each related paper, the authors claim their method performs the best and demonstrate through ablation experiments that the singular parts they identify should be adjusted.

This is quite interesting. From a paper writing perspective, the authors need to maintain logical consistency, ensuring that the useful parts they emphasize are validated in the ablation experiments. However, the confusion arises from the fact that there should not be such significant differences between these methods. The results of each study seem to support different strategies for adjusting singular directions, which complicates the issue further. This suggests that how to effectively select and adjust singular directions remains a controversial and not fully resolved key issue.

Given this, let us take an observer’s perspective and simply analyze which parts may be more useful in LoRA initialization. Intuitively, top singular directions indeed contain the most useful information learned by the model during the pre-training process. The purpose of fine-tuning is to leverage this knowledge gained during pre-training. Therefore, directly adjusting these important singular directions may disrupt the effectiveness of this information, leading to poor fine-tuning results.

I have personally found this in my experiments: adjusting top singular directions usually does not yield significant performance gains and can sometimes even negatively impact model performance. This indicates that preserving the structure of these directions during fine-tuning may be more important than over-adjusting them. Thus, exploring other methods of adjusting singular directions may be a more effective strategy.

Let’s focus on fine-tuning randomly selected singular vectors and bottom singular vectors. Logically, I agree that fine-tuning bottom singular vectors seems more reasonable.

Firstly, bottom singular vectors usually represent less important or secondary information learned by the model during pre-training. Therefore, fine-tuning these vectors will not interfere with the key information captured by the model during pre-training. This helps preserve the core knowledge gained during pre-training.

Secondly, by fine-tuning these less important parts, we can transform “useless into useful,” allowing these vectors to play a role in downstream tasks, capturing information relevant to specific tasks.

This strategy can add new, targeted information to the task while maintaining the core capabilities of the pre-trained model. Thus, fine-tuning bottom singular vectors may theoretically be an effective way to retain existing knowledge while introducing task-related adjustments. In contrast, the method of randomly selecting singular vectors, while exploratory, may not be as stable or targeted as fine-tuning bottom singular vectors.

However, I vaguely recall that I have seen these analyses in LoRA.

1.2 Review of LoRA

Upon rereading Section 7 of LoRA, I found some content that validates the above analysis. For instance, LoRA points out that the role of is to expand the unimportant directions in the weight matrix W. This further proves that during fine-tuning, top singular vectors should not be chosen for adjustment.

At the same time, LoRA demonstrates through extensive experiments that the content truly learned during fine-tuning is task-specific directions (TSD), which are crucial for downstream tasks. Therefore, our focus of adjustment should be on TSD, rather than top, bottom, or random singular vectors.

However, there are some contradictions in LoRA’s description of TSD. For example, LoRA states that TSD are singular directions of the weight matrix , while also defining TSD as . Moreover, LoRA believes that TSD may include some task-irrelevant directions, although this statement seems somewhat contradictory and absurd.

These inconsistencies have prompted us to think further. We believe the root of the problem lies in the unclear definition of TSD—there are actually ambiguities in the fundamental definitions of the entire framework (such as matrix directions, etc.). Therefore, we decided to redefine a clearer framework from scratch as the cornerstone of TSD theory and build a complete TSD system on this basis.

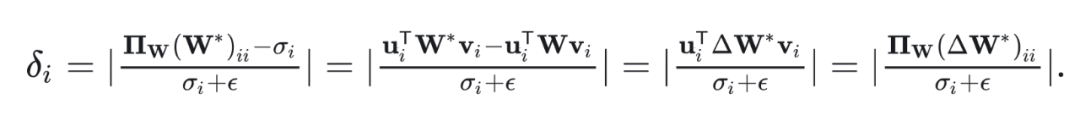
Building a Framework for Task-Specific Directions from Scratch

2.1 Definition of TSD

First, the basis and direction of a matrix are defined as follows:

Definition 1: For a matrix , its left singular vectors and right singular vectors are represented by matrices and , respectively. The basis of matrix is defined as follows: Core basis: The core basis of matrix is defined as , where each is a rank-1 matrix constructed from the singular vectors and . Global basis: The global basis of matrix is defined as for all , covering all combinations of left and right singular vectors.

Definition 2: The direction of the matrix (where ) is based on its global basis definition, using an extended set of its singular values , filled with zeros, specifically represented as , i.e., flattened through rows.

Note that any global basis can be viewed as a unit direction, as its direction is a one-hot vector. Hence, we also refer to the core (global) basis as core (global) directions.

We know that for any specific task, there exists an optimal matrix in the matrix space . For the pre-trained weight matrix , its optimal adjustment for that task is . In PEFT, we can only obtain information about and its direction. Since and are based on their respective bases, we first project both onto the global basis of .

Definition 3: The definition of is the projection of a direction in one coordinate system onto another coordinate system. In particular, is the projection of the direction of matrix onto the global basis of matrix .

Based on the global basis of matrix , represents the direction that needs to evolve. Since can only utilize at most core bases, it can only change values of its direction. Therefore, the focus is on the changes in core directions.

During the transformation process, the degree of change in the coordinate values of different core directions varies, influenced by the diversity of downstream tasks; some core directions may change significantly while others change little. The defined change rate measures the degree of change in the th core direction:

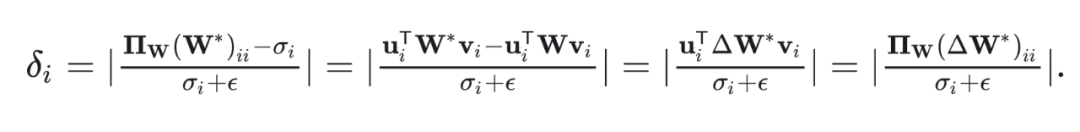
Therefore, we can define TSD as:

Definition of TSD: For a specific task and pre-trained weight matrix , assuming the optimal weight for that task is , then the task-specific direction (TSD) for that task on refers to those core directions that exhibit a significantly high change rate during the transition from to .

From the definition of TSD, we can directly draw the following conclusions:

• TSD is a subset of core directions of the pre-trained weight W. They are task-relevant, meaning that TSD varies across different tasks but remains fixed for a particular task.

• Core directions associated with larger singular values are less likely to be identified as TSD because their coordinate change rates are usually smaller than those associated with smaller singular values.

With the definition of TSD established, we can further explore the properties of TSD.

2.2 Properties of TSD

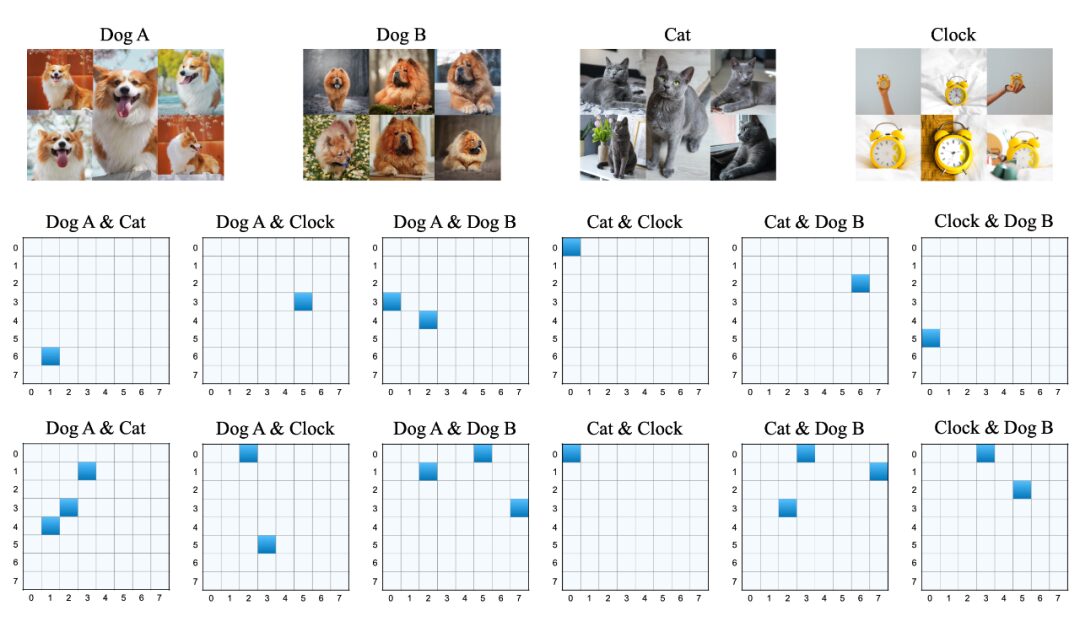
We assume that through full fine-tuning, we can obtain optimal weight, , by fully fine-tuning LLaMA-7B on commonsense reasoning tasks, we ultimately calculate the change rates for each direction, as shown in the figure below:

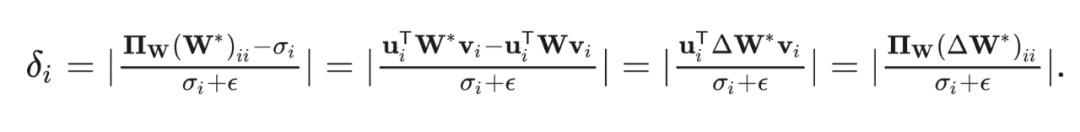
Firstly, the left side of the graph shows the change rate for each direction, with the horizontal axis representing the index of singular values, which decreases as the index increases. It is evident from the graph that directions with larger change rates are mostly concentrated at smaller singular value index positions.

However, the middle graph indicates that smaller singular values do not always accompany larger change rates, suggesting that the relationship between change rate and singular value size is not a simple linear one. The rightmost graph ranks the change rates of all directions from largest to smallest, clearly showing that TSD occupies only a very small number of directions, while most directions have negligible change rates. This indicates that during fine-tuning, only a few directions have a significant impact on the task, while the change rates of most directions can be virtually ignored. Therefore, we can draw two properties of TSD:

• TSD primarily corresponds to core directions associated with smaller but not minimal singular values.
• TSD encompasses only a few directions, which exhibit significant change rates during the transition from to , while the change rates of most other core directions are small or negligible.

One more thing, are TSD truly task-specific?

To investigate this, we adopted a typical example: subject-driven generation tasks. In this setup, we tracked the TSD captured when different subjects were targeted and analyzed the relationships between these TSD.

The first row of this figure displays images of different subjects. The second and third rows show the results extracted from two different layers of the U-net model. Each subplot illustrates the similarity of TSD captured by two different subjects. The title of each subplot indicates the corresponding subject, with the direction order of the first subject represented by columns and the direction order of the second subject represented by rows. The deep blue areas highlight the parts where the directions of the two subjects overlap.

The experimental results confirm the task specificity of TSD; each task exhibits different TSD, with minimal overlap between tasks. Furthermore, even when tasks share the same direction, the importance of these directions varies significantly across different tasks. For instance, as shown in the first subplot of the second row, “Dog A” and “Cat” share a common direction, but for “Dog A,” this direction ranks seventh in importance, while for “Cat,” it ranks second.

Moreover, closely related tasks often share more directions, such as between “Dog A” and “Dog B”; however, the importance of these shared directions still differs for each task. This variability further emphasizes the task specificity of TSD, showcasing their uniqueness and variable impact in different contexts.

2.3 Challenges of Using TSD

Despite our in-depth exploration of the definition and properties of TSD, a significant challenge lies in the fact that prior to fine-tuning, both and are unknown, meaning that it is nearly impossible to utilize TSD information in practical fine-tuning scenarios ahead of time.

Despite this apparent challenge, we did not stop there but rather placed our hopes on . We hypothesize that the core directions with the highest change rates predicted by LoRA in are closely related to TSD. To validate this hypothesis, we conducted two types of experiments.

First, we wanted to know whether the top 8 directions predicted based on included the top 4 directions with the highest change rates in TSD; we called this metric recall. We also wanted to know whether the top 8 directions predicted based on all fell within the top 16 directions with the highest change rates in TSD; we called this metric accuracy. The experimental results are shown in the figure below:

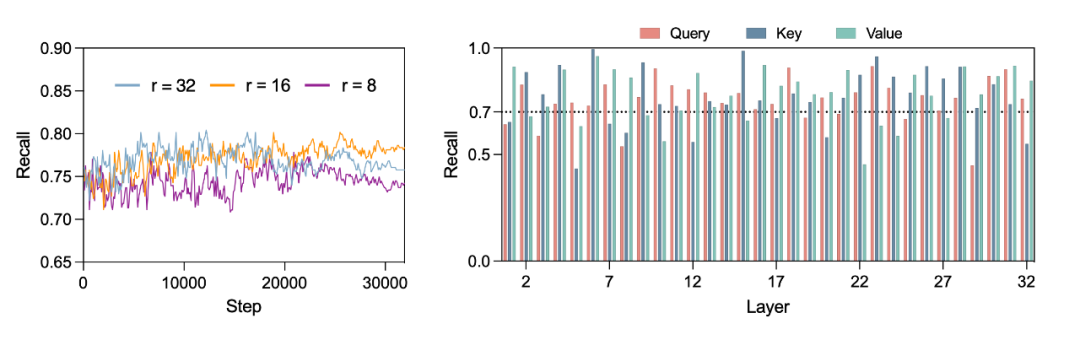
For example, regarding accuracy: during the LoRA fine-tuning process, we tracked the accuracy of the predicted directions in the query, key, and value layers of the LLaMA-7B model every 100 training steps, analyzing the continuously updated ability to capture TSD.

The left graph displays the average accuracy across all query, key, and value layers, showing the model’s ability to maintain task-specific knowledge at each training step. Under different LoRA rank settings, these accuracies consistently exceed 0.75, indicating that can reliably capture and integrate TSD information.

The right graph calculates the average accuracy of each query, key, and value layer across all training steps for the case where the rank setting is r=32, revealing their sensitivity to TSD. The average accuracy of most layers remains above 0.75, demonstrating their robustness in capturing TSD information.

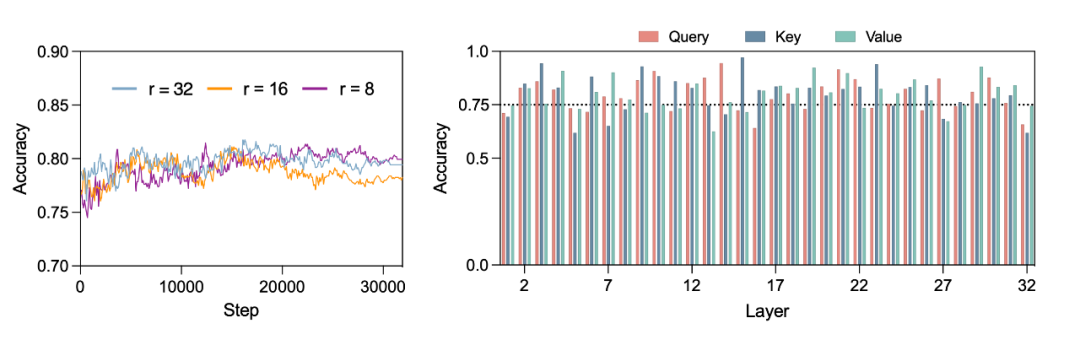
This indicates that can not only capture the parts with the highest change rates in TSD, but also that the directions it captures are overall among the top change rates of TSD. This leads to an important conclusion:

Regardless of the rank settings of LoRA, training steps, or specific layers in the model, can always capture information about task-specific directions (TSD).

This conclusion is exciting, indicating that even without prior knowledge of TSD, we can still capture these key task-specific information through the obtained during the LoRA training process.

LoRA-Dash: Further Unlocking the Potential of TSD

To accelerate learning efficiency in TSD directions and alleviate the learning burden of , we propose a new method—LoRA-Dash. This method aims to capture task-specific directions more efficiently, thereby enhancing the speed and effectiveness of the fine-tuning process.

LoRA-Dash consists of two main stages:

• “Pre-Launch Stage”: In this stage, TSD is identified, which is a key part of model optimization, ensuring that the most needed directions for adjustment are found. Specifically, LoRA-Dash utilizes the obtained after updates to predict TSD and determine the directions that need optimization in the next stage.

• “Sprint Stage”: In this stage, the model fully utilizes the previously identified TSD for fine-tuning optimization, allowing the pre-trained model to better adapt to specific tasks. Specifically, LoRA-Dash directly simulates the coordinate changes of TSD, accelerating the model’s adaptive adjustments in new tasks, thereby significantly improving its performance.

The pseudocode for LoRA-Dash is as follows:

Experiments

We conducted experiments on commonsense reasoning, natural language understanding, and subject-driven generation tasks.

The experimental results show that LoRA-Dash achieves performance improvements far exceeding those of LoRA across various tasks. The results demonstrate the effectiveness of TSD for downstream tasks, with LoRA-Dash fully unlocking the potential of TSD, further stimulating performance levels for efficient fine-tuning.

Commonsense Reasoning (fine-tuning with LLAMA-7B, LLAMA2-7B, and LLAMA3-8B):

Natural Language Understanding (fine-tuning with DeBERTaV3-base and DeBERTaV3-large):

Subject-Driven Generation (fine-tuning with SDXL):

We also conducted a series of experiments. First, we explored the relationship between the directions determined in the pre-launch stage and the final directions after the sprint stage, aiming to determine whether LoRA-Dash can amplify TSD information, and if so, to what extent this amplification occurs.

Next, we compared the effectiveness of different directions (such as those with maximum or minimum singular values) and analyzed the impact of the length of the pre-launch stage and the number of directions in the sprint stage on performance.

Finally, we verified whether the information in TSD could enhance the performance of other methods. For more details, please refer to the original text.