Today, we continue our work on fixed-point programming, which is quite significant for using PR control, especially since floating-point microcontrollers are expensive.
Previously, in floating-point development, we discussed the discretization and code implementation of the Proportional Resonant Controller (QPR).
For fixed-point implementation: Considering quantization errors, we directly run the IIR2 function of the PR controller on IQ26, which provides a fourfold increase in precision compared to single-precision floating-point. The integer representation can handle a maximum of 32 digits, which is sufficient to meet the output dynamic range of the PR control. If necessary, we can also directly scale the PR output by 2^N to satisfy the modulation range of the controller.
IIR2 Definition:
typedef struct IIR_2ORDER_IQ_TAG{
Uint16 coeff_init_flag;
_iq filter_out;
_iq filter_W0;
_iq filter_W1;
_iq filter_W2;
_iq coeff_B0;
_iq coeff_B1;
_iq coeff_B2;
_iq coeff_A1;
_iq coeff_A2;
}IIR_2ORD_IQ_DATA_DEF;
Function:
static inline _iq iir2_IQ_func_(volatile _iq input, volatile IIR_2ORD_IQ_DATA_DEF *p)
{
//
// w0 = x(0) – A1 * W1 – A2 * W2
//
p->filter_W0 = input – _IQ26mpy(p->coeff_A1, p->filter_W1) – _IQ26mpy(p->coeff_A2, p->filter_W2);
//
// Y(0) = Gain * (B0 * W0 + B1 * W1 + B2 * W2)
//
p->filter_out = _IQ26mpy(p->coeff_B0, p->filter_W0) + _IQ26mpy(p->coeff_B1, p->filter_W1) + _IQ26mpy(p->coeff_B2, p->filter_W2);
//
// Update last data
//
p->filter_W2 = p->filter_W1;
p->filter_W1 = p->filter_W0;
return(p->filter_out);
}
PR Control Coefficient Calculation, using floating-point numbers for input, makes debugging parameters much easier. The IQ26 coefficient calculations are performed within this function:
static inline void updata_pr_ctrl_coeff_IQ( volatile IIR_2ORD_IQ_DATA_DEF *p,
float32 kr,
float32 wc,
float32 wr,
float32 kp,
float32 ts)
{
// with KP gain
float32 ts_x_ts = ts * ts;
float32 wr_x_wr = wr * wr;
float32 div_x = ts * ts * wr * wr + 4.0f * wc * ts + 4.0f;
#if 1
p->coeff_B0 = _IQ26((4.0f * kp + kp * ts_x_ts * wr_x_wr + 4.0f * kp * ts * wc + 4.0f * kr * wc * ts)/div_x);
p->coeff_B1 = _IQ26(-1.0f * (8.0f * kp – 2.0f * kp * ts_x_ts * wr_x_wr)/div_x);
p->coeff_B2 = _IQ26((4.0f * kp + kp * ts_x_ts * wr_x_wr – 4.0f * kp * ts * wc – 4.0f * kr * ts * wc)/div_x);
p->coeff_A1 = _IQ26((2.0f * ts_x_ts * wr_x_wr – 8.0f)/div_x);
p->coeff_A2 = _IQ26((ts_x_ts * wr_x_wr – 4.0f * ts * wc + 4.0f)/div_x);
#else
// without KP gain
float32 coeff_B0 = (4.0f * kr * wc * ts)/div_x;
float32 coeff_B1 = 0;
float32 coeff_B2 = -1.0f * p->coeff_B0;
float32 coeff_A1 = (2.0f * ts_x_ts * wr_x_wr – 8.0f)/div_x;
float32 coeff_A2 = (ts_x_ts * wr_x_wr – 4.0f * ts * wc + 4.0f)/div_x;
p->coeff_B0 = _IQ(coeff_B0);
p->coeff_B1 = _IQ(coeff_B1);
p->coeff_B2 = _IQ(coeff_B2);
p->coeff_A1 = _IQ(coeff_A1);
p->coeff_A2 = _IQ(coeff_A2);
#endif
}
PR Data Structure Definition
typedef struct PR_CTRL_LAW_DATA_IQ_TAG{
IIR_2ORD_IQ_DATA_DEF f_1st;
IIR_2ORD_IQ_DATA_DEF f_3st;
IIR_2ORD_IQ_DATA_DEF f_5st;
IIR_2ORD_IQ_DATA_DEF lead_lag_comp;
_iq f1stOut;
_iq f3rdOut;
_iq f5thOut;
_iq max;
_iq min;
_iq pr_ctrl_out;
}PR_CTRL_IQ_DATA_DEF;
PR + Lead-Lag Compensation:
static inline _iq pr_ctrl_IQ_func( _iq error, PR_CTRL_IQ_DATA_DEF *p)
{
const _iq error_iq26 = _IQmpy4(error);
p->f1stOut = iir2_IQ_func_(error_iq26, &p->f_1st);
p->f3rdOut = iir2_IQ_func_(error_iq26, &p->f_3st);
p->f5thOut = iir2_IQ_func_(error_iq26, &p->f_5st);
p->pr_ctrl_out = (p->f1stOut + p->f3rdOut + p->f5thOut);
p->pr_ctrl_out = iir2_IQ_func_(p->pr_ctrl_out, &p->lead_lag_comp);
_IQsat(p->pr_ctrl_out, p->max, p->min);
return(_IQdiv4(p->pr_ctrl_out));
}
Overall Parameter Calculation for PR Control Function:
static void pr_ctrl_coeff_IQ_func(
PR_CTRL_IQ_DATA_DEF *p,
float32 grid_freq,
float32 kp,
float32 kr,
float32 ts,
float32 lead_fz,
float32 lead_fp,
float32 max,
float32 min)
{
updata_pr_ctrl_coeff_IQ(&p->f_1st, kr, 2.0f * M_PI, 2.0f * M_PI * grid_freq, kp, ts);
updata_pr_ctrl_coeff_IQ(&p->f_3st, kr, 2.0f * M_PI, 2.0f * M_PI * grid_freq * 3.0f, kp, ts);
updata_pr_ctrl_coeff_IQ(&p->f_5st, kr, 2.0f * M_PI, 2.0f * M_PI * grid_freq * 5.0f, kp, ts);
float32 ts_x_wz = ts * 2.0f * M_PI * lead_fz;
float32 ts_x_wp_puls_2 = ts * 2.0f * M_PI * lead_fp + 2.0f;
p->lead_lag_comp.coeff_B0 = _IQ((ts_x_wz + 2.0f)/ts_x_wp_puls_2);
p->lead_lag_comp.coeff_B1 = _IQ((ts_x_wz – 2.0f)/ts_x_wp_puls_2);
p->lead_lag_comp.coeff_B2 = 0;
p->lead_lag_comp.coeff_A1 = _IQ((ts * 2.0f * M_PI * lead_fp – 2.0f)/ts_x_wp_puls_2);
p->lead_lag_comp.coeff_A2 = 0;
p->max = _IQ(max);
p->min = _IQ(min);
p->pr_ctrl_out = 0;
}
Running Tests:
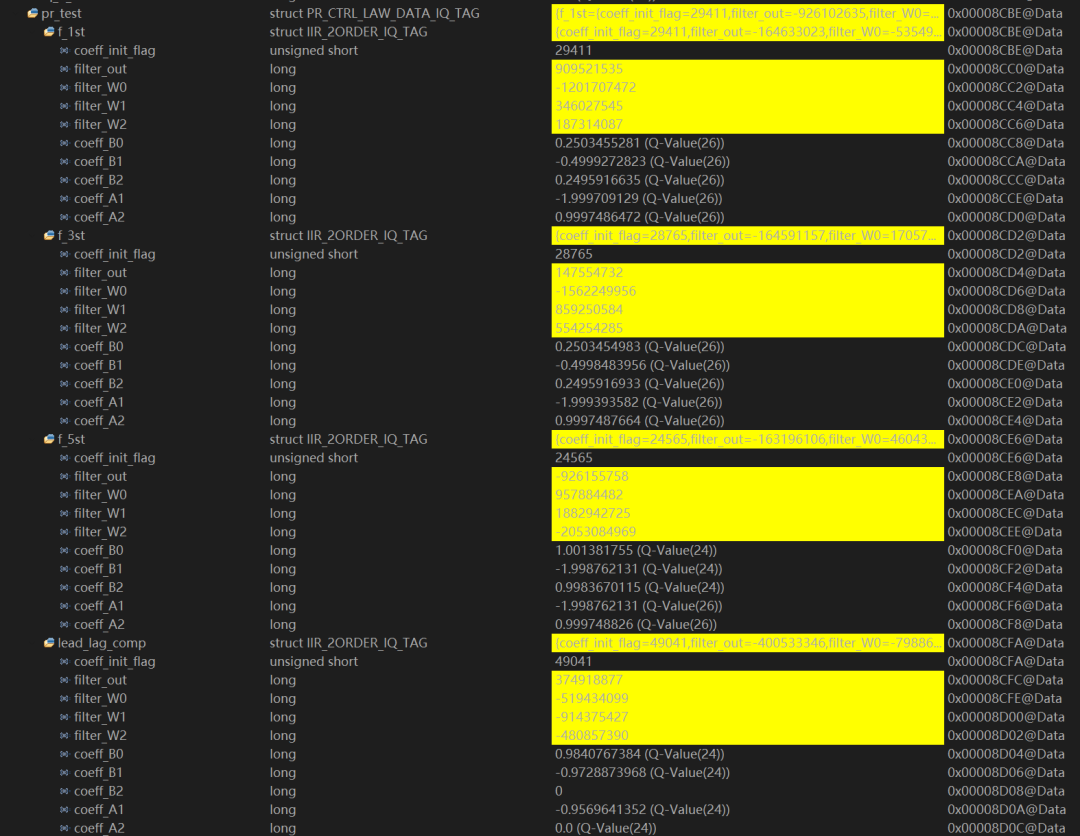
Comparison with MATLAB:
The discretization coefficients of the PR function are compared; the upper part is the coefficients converted using MATLAB’s built-in functions, while the lower part shows the coefficients converted as described above. The results from the DSP show that after adapting to IQ26 conversion, the coefficients maintain high precision.
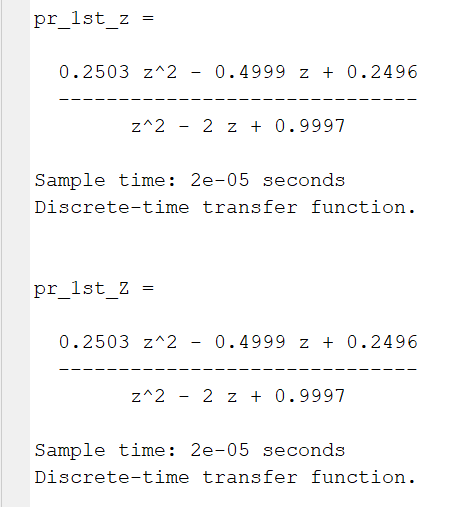
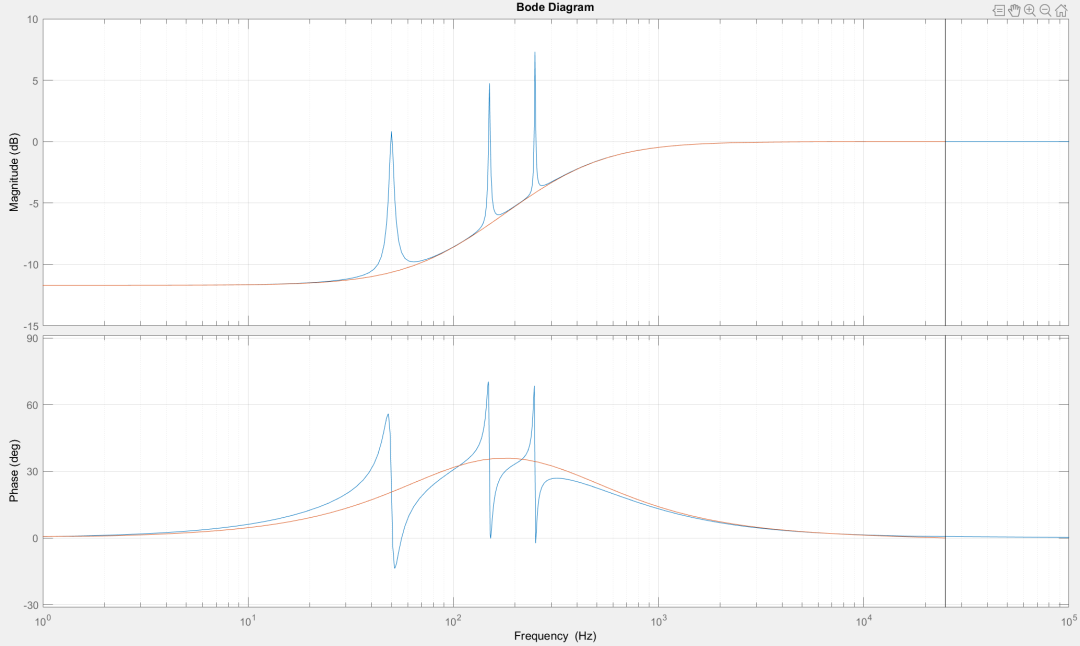
Adapting the PR control with 135 iterations to recombine the lead-lag compensator to address the instability caused by phase jumps in the PR.
My abilities are limited, and I am currently learning fixed-point programming. If there are any mistakes, please kindly point them out. Thank you.